【中1数学・式の計算】文字式と数の足し算・引き算を使いこなそう!
ご覧いただきありがとうございます、学習塾ONEDAYです。
文字式の計算を扱うシリーズの第3弾です。初回は文字式を作るパーツとして、項と係数、次数の話をしました。そして第2回にあたる前回は文字式と数をかけたり割ったりする計算をできるようにしていきましたね。まだ見てない方はこちらの記事をご覧ください!
▼前回の記事
第3回である今回は文字式の足し算・引き算です。それでは始めましょう!
文字式の足し算・引き算
文字が同じ項は係数を足し引きしてまとめられる
$${例1 4x + 2x}$$
まずは一番簡単な2つの文字式の足し算から始めましょう。$${ 4x }$$、$${ 2x }$$は$${ x }$$ がそれぞれ4個、2個ですね。そこで前回の記事と同じように、この2つの文字式を線分図で表してみたいと思います。

この線分図を見ると、$${ x }$$を1目盛りと考えたとき、2つの文字式で目盛りの大きさは同じであることがわかります。そして、目盛り$${ x }$$の数は合わせて$${ 4+2=6 }$$より6個なので、答えは$${ 6x }$$となります。
つまり、文字式の足し算では、文字が全く同じときにその係数同士を足して、後から文字をくっつければ答えが完成します。
$${例2 4x + 2y}$$
では例2の場合はどうでしょうか?例2の式は例1の$${ 2x }$$の部分について、文字を変えて$${ 2y }$$としています。つまり、先ほどの式と違って、項に含まれる文字が違うパターンですね。
結論を先に言ってしまうと、実は例2の式をこれ以上計算して簡単にすることはできません。その理由は、例2の式を線分図にして、例1の線分図と見比べてみるとわかるでしょう。
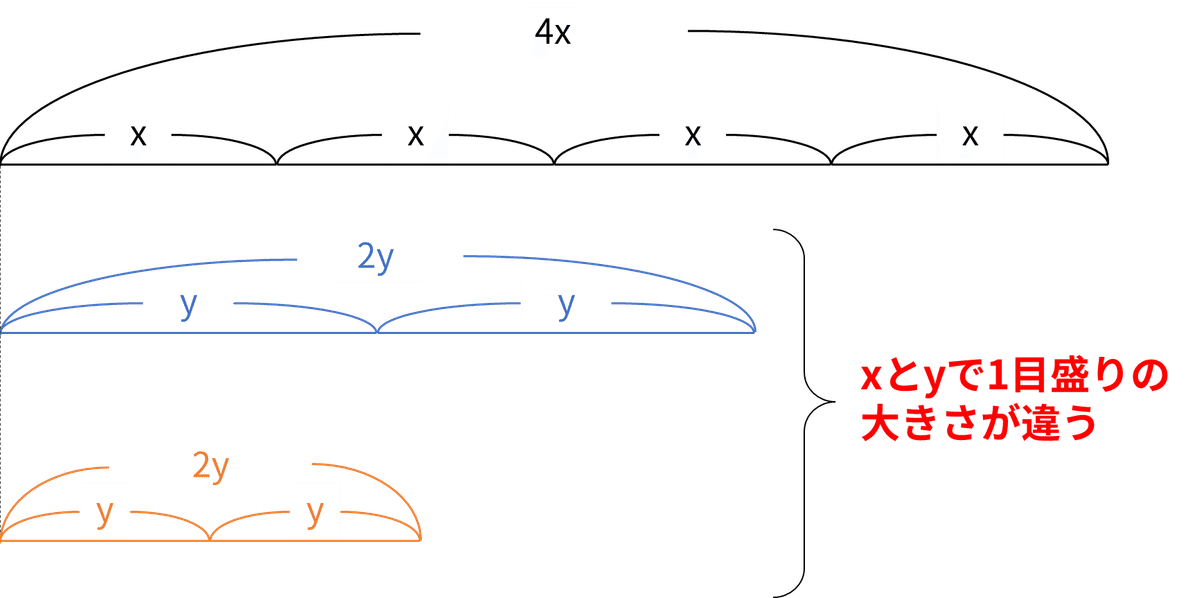
この図を見ると、青線のように$${ y }$$が$${ x }$$よりも大きいこともあれば、赤線のように$${ y }$$が$${ x }$$よりも小さいこともあり得ます。
つまり、文字が違えば1目盛りの大きさも変わってしまうので、合わせて目盛りが○個という数え方ができなくなってしまうのです。
文字が同じでも指数が違うと足し引き出来ない
$${例3 4x - 5x}$$
$${例4 4x - 5x^2}$$
次に例3と4の式を比べてみましょう。例3は2つの項のどちらも文字の部分が$${ x }$$なので、文字の形は全く同じですね。したがって
$${ 4x - 5x =(4-5)x = -x }$$
と係数の引き算をしてひとつの項にまとめることができます。
一方で、例4を見てみると、使っている文字はどちらも$${ x }$$で、しかも出てくる係数も例3と同じになっています。ぱっと見「例3と同じじゃない……?」と思うかもしれませんが、右側の項が$${ -5x^2 }$$、つまり指数の2が$${ x }$$にくっついているところだけ違います。
実は、このたったひとつの指数がつくだけでこの式はこれ以上計算できなくなってしまいます。というのも、ふたつの項を見比べると文字の部分はそれぞれ$${ x }$$と$${ x^2 }$$ですが、このふたつは大きさが異なる場合があるからです。
試しに$${ x=3 }$$とすると、$${ x^2 = 3^2 = 9 }$$となってしまい、$${ x }$$と$${ x^2 }$$は異なる数になっていますね。
ここまでの話をまとめると、項を足したり引いたりするためには、文字だけでなくその文字の指数も同じでないといけないということが言えます。
項をまとめて式を簡単にする
$${例5 12x^2 + 8y - 18x + 3y + 5x^2}$$
最後に文字式の足し算・引き算をどのように使うか簡単に説明します。例5の多項式は項が5つあって、お世辞にも見やすい式とは言いがたいですね。
しかし、今までの話から、同じ文字・指数の項は係数どうしを足したり引いたりしてまとめることができましたね。そこで、同じ文字・指数の項に色をつけると、$${ x^2 }$$の項(赤色)が2つ、$${ x }$$の項(緑色)が1つ、$${ y }$$の項(青色)が2つあることがわかります。
同じ仲間の項はまとめられますから、あとは以下の式のように係数どうしを計算して、最終的に5つあった項を3つまで減らすことができました。

このように、放置しておくと項が無駄に増えがちな多項式について、項同士を足し引きしてまとめることで、見やすい式に整理することができるのです。
まとめ
文字式の足し算・引き算で学んだことは以下の通りですね。
文字と指数の組み合わせが全く同じ場合、係数どうしを足したり引いたりすることで項をまとめることができる
使っている文字が同じでも指数が違うと、それ以上計算できない
たくさん項が出てきた場合、足し算・引き算を使って項をまとめることで式を短くわかりやすい形にできる
特に2つ目の指数の違いは注意してみないと「あ、うっかり見落として計算しちゃった……」といった具合に、本来まとめられない項をまとめてしまったり、逆にまとめられる項をまとめ忘れたりしてしまいかねません。
なので、文字だけでなく特に指数を注意して確認するとミスが減らせると思います。あとは練習あるのみ、ということで、練習問題に行ってみよう!
練習問題
(1) $${ 2.4x^2 + 4.8x^2 }$$
(2) $${ 2.8y - 9.8y }$$
(3) $${ 8x + 6x - 4x }$$
(4) $${ 2y^4 - 9y^4 + 7y^4 }$$
(5) $${ -3.2a^2 + 9.6a - 6.4a^2}$$
(6) $${ -\frac{5}{4}x^3 + \frac{3}{4}x^2 - \frac{3}{4}y +\frac{7}{8}x^3 -\frac{1}{4}y }$$
学習塾ONEDAYの案内
最後になりますが、当塾では勉強に不安を抱えている方の学習支援を行なっています。Google meetを用いたオンライン授業により、日本全国の皆さんに学習支援を提供できる体制を整えておりますので、まずはこちらからお気軽にお問い合わせ下さい!
学習相談窓口
ONEDAY公式LINE:https://lin.ee/nqPLhp3
ONEDAY公式サイト:https://oneday-cram.com
練習問題の答え
(1) $${ 7.2x^2 }$$
(2) $${ -7y }$$
(3) $${ 10x }$$
(4) $${ 0 }$$
(5) $${ -9.6a^2 + 9.6a }$$
(6) $${ -\frac{3}{8}x^3 + \frac{3}{4}x^2 - y }$$
