Python で「パスカルの三角形」を味わい尽くす

パスカルの三角形

　パスカルの三角形を書けば $${(a+b)^n}$$ の展開式の各項の係数を簡単に求めることができる。その手順は、

○　各段両端は 1 。　　　　　　　　　　　　　　　… (1)
○　上段の２数の和を、２数の真ん中下段に書く。　… (2)
○　これを繰り返す。

これだけである。

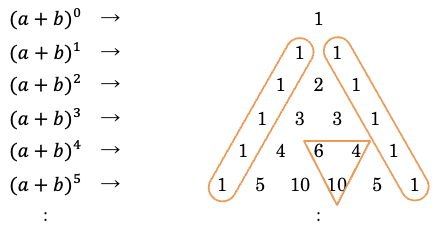
　上から n 段目の数が $${(a+b)^n}$$ の展開式の各項の係数というわけである。たとえば、
　　　$${(a+b)^n=a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5}$$
という具合である。
　そして、こんな単純な操作なら、それこそコンピュータにやらせたい。そこで Python の出番である。

　ところで、高校数学で「２項定理」を学ぶ。

《２項定理》
$${(a+b)^n}$$ の展開式の $${a^{n-r}b^r}$$ の係数は $${_n\textup{C}_r\quad(r=0,1,2,…,n)}$$

　つまり、パスカルの三角形に書かれた数は、組み合わせ $${\textup{C}}$$ の数だということ。これを知っているなら、パスカルの三角形の理解も深まるだろう（とは言え、２項定理を知らなければパスカルの三角形が分からないという訳でもない）。
　では、ここで【問題】です。

〈パスカルの三角形〉の上から $${n}$$ 段目、左から $${r}$$ 列目の数を  $${\textup{c}(n,r)}$$ と表すことにしよう。
　さて、上の〈パスカルの三角形の書き方〉の (1) と (2) を  $${\textup{c}(n,r)}$$ を使って書くと、どうなる？

　〈答え〉は次のようになる。

○　$${\textup{c}(n,0)=1\qquad\textup{c}(n,n)=1}$$　　　　　　　… (1)
○　$${\textup{c}(n,r)=\textup{c}(n-1,r-1)+\textup{c}(n-1,r)}$$　… (2)

〈参考〉組み合わせ $${\textup{C}}$$で書くなら、
○　$${_n\textup{C}_0=1\qquad_n\textup{C}_n=1}$$　　　　　　　　　… (1)
○　$${_n\textup{C}_r=\,_{n-1}\textup{C}_{r-1}+\,_{n-1}\textup{C}_r}$$　　　　　　　… (2)
（組み合わせ $${_n\textup{C}_r}$$ での説明は こちら をご覧ください）

再帰関数で表そう

　このように数列の漸化式のように書けるということは「再帰関数で表せる」ということだ。では、さっそくやってみよう。

def c(n,r):                          # 上の(1),(2)をもとに再帰関数を定義
    if (r==0)or(n==r):               # これが(1)、終了条件（数列風に言うと、初項）
        return 1
    return c(n-1,r-1)+c(n-1,r)       # これが(2)、漸化式本体

n=int(input('何段目？　'))              # ここからプログラム本体
r=int(input('何列目？　'))
print(c(n,r))                        # ここで関数を呼び出している

　さらに $${(a+b)^n}$$ の展開式を丸ごと書いてみよう。

def c(n,r):                                  # 再帰関数を定義
    if (r==0)or(n==r):
        return 1
    return c(n-1,r-1)+c(n-1,r)

n=int(input('(a+b)の何乗？　'))                  # ここからプログラム本体
print('(a+b)^',n,'=a^',n,end='+')
for r in range(1,n):
    print(c(n,r),'a^',n-r,'b^',r,end='+')    # ここで関数を呼び出している
print('b^',n)

正規分布のグラフ

　なお、 $${(a+b)^n}$$ の展開式の係数だけを左から順に取り出してグラフにすると、正規分布のようなグラフになる（数学的に正しく表現すると「二項分布」と呼ぶ）。

def c(n,r):
    if (r==0)or(n==r):
        return 1
    return c(n-1,r-1)+c(n-1,r)

import matplotlib.pyplot as plt      # グラフを描く機能をインポート
n=int(input('(a+b)の何乗？　　'))
for r in range(n+1):
    plt.bar(r,c(n,r))                # 関数を呼び出しながら棒の長さを指定
plt.show()　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　# グラフ描画

　このプログラムを実行して $${n=10}$$ を入力したところ、次のようなグラフを描いた。正規分布っぽく見えるだろう。お試しあれ。

※　ところで、このグラフに関しては Python を使うより、エクセルでやりたいところである。すごくシンプルにできる。こちら をご覧あれ。

パスカルの四面体

　ところで、《２項定理》があるなら《３項定理》もある。

《３項定理》　$${(a+b+c)^n}$$ の展開式 $${a^pb^qc^r}$$ の係数は  $${\dfrac{n\textit{!}}{p\textit{!}\:q\textit{!}\:r\textit{!}}}$$
　　　　（ただし $${p,q,r}$$ は負でない整数で $${p+q+r=n}$$）

　そして $${(a+b)^n}$$ の展開式の係数を手早く知るためのパスカルの三角形があるなら、$${(a+b+c)^n}$$ の展開式の係数を手早く知るための パスカルの四面体 なるものがあっても良いだろうと考えて、作ってみた。

　上図中の側面 $${Oab\,,\,Obc\,,\,Oca}$$ はいずれも通常のパスカルの三角形と同じである。違うのは四面体の底面にあたる部分で、すぐ上の３つの数を順繰り足したものが $${(a+b+c)^n}$$ の展開式の係数になる。上図・下式の通りである。

$${\small{(a+b+c)^4=(a^4+b^4+c^4)+4\,(a^3b+b^3c+c^3a+ab^3+bc^3+ca^3)}}$$
　　　　　　$${\small{+\,6\,(a^2b^2+b^2c^2+c^2a^2)+12\,abc\,(a+b+c)}}$$

　さて、先ほど「パスカルの三角形」でやったのと同じようなこと、つまり「再帰関数」を作ったり、$${(a+b+c)^n}$$ の展開式を表示したり、さらには係数をグラフ化したり、そんなことを「パスカルの四角形」でも出来るかな。（私はパスしたい 。。。）

フラクタル画像

　再帰関数（自分を呼び出す関数）と相性が良いのがフラクタル（自己相似形）画像、その中でも形がパスカルの三角形に似ているのが シェルピンスキーのギャスケット 。

　本来この図形の作り方は「大きな正三角形から、その４分の１の逆三角形をくり抜くという操作を（無限回）繰り返す」のだが、ここでは文字「▲」と「　」（空白）をたくさん書くことで成し遂げた次第である。また「▲」を２つ並べれば（▲▲）、その間に自然と「▽」が見えることも利用している。

n=int(input("何段？ "))
dan="▲"
for i in range(n):
    print(dan)
    s="▲"                       # 左端に "▲"
    for j in range(i):
        if dan[j]==dan[j+1]:
            s=s+"　"
        else:
            s=s+"▲"
    dan=s+"▲"                   # 右端に "▲"

※　上のコードの１行目の input 文で「128」と入力して、128（ $${=2^7}$$）段の図形を描いた。コードを実行して得た文字列をワードに貼り付けて、中揃えにして、行間隔・文字間隔を調整したものが上図である。

　そして、私がこれを思いついたのは「パスカルの三角形」との類似性。私にとってヒントはそこにあった。

○　各段両端は 1 。　　　　　　　　　　　　　　　… (1)
○　上段の２数の和を、２数の真ん中下段に書く。　… (2)

　パスカルの三角形では「各段両端に 1 … (1) 」を書くが、ここでは「各段両端に ▲ 」を書いている。
　また、パスカルの三角形では「上段の２数の和を、２数の真ん中下段に書く … (2) 」が、ここではコードの７行目〜10行目で、こう（↓）している。

if dan[j]==dan[j+1]:    # 真上にある２つの文字が同じ（ ▲ と ▲ 、または 空白 と 空白 ）なら、
    s=s+"　"             　#     空白を書き、
 else:                  # 同じでない（ ▲ と 空白 、または 空白 と ▲ ）なら、
    s=s+"▲"             #     ▲ を書く

　これについては「なんだか似ているな」と思っていただければ、それで十分。気になる人はやっていただいても良いし、「ふーん」と流していただいても良い。
※　要は、パスカルの三角形の奇数の部分を「▲」で、偶数の部分を「　」（空白）で置き換えている・・・このようにも言える。

パスカルの賭け

　パスカル（1623～1662）といえば「人間は考える葦である」という言葉で有名です。パスカルが書いた「パンセ」という本の中の一節です。
　パスカルは「パンセ」の中で「神を信じるのと信じないのではどちらが得か？」を計算しています。「パスカルの賭け」と呼ばれています。それについては、こちら（↓）をご覧ください。（パスカルの三角形とも Python とも関係ありませんが、パスカルつながりということで）

※　俗に「神の存在証明」と呼ばれることもありますが、実際には証明したわけではありません。彼の前提に則って「どちらが得か、損か？」の期待値計算をしたのです。

　以上、Python で「パスカルの三角形」を味わい尽くしてくださいな。