重複順列と重複組合せ

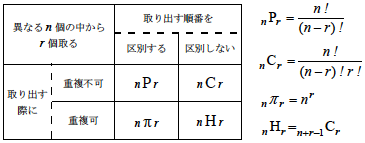
　このうち順列 $${\boldsymbol{_n}\mathbf{P}\boldsymbol{_r}}$$ と組合せ $${\boldsymbol{_n}\mathbf{C}\boldsymbol{_r}}$$ については教科書にも載っているし、練習もしているだろうからここでは説明せずに、重複順列 $${\boldsymbol{_n}\large{\mathbf{\pi}}\boldsymbol{_r}}$$ と重複組合せ $${\boldsymbol{_n}\mathbf{H}\boldsymbol{_r}}$$ について簡単に説明しよう。

重複順列と重複組合せ

◇　重複順列 $${\boldsymbol{_n}\large{\mathbf{\pi}}\boldsymbol{_r}}$$
例：大中小３個のサイコロを投げて出る目の場合の数は、₆π₃ ＝ 6³ ＝216通り
一般に、異なる n 個の中から重複を許して r 個取り出す（順番を区別する）
→　$${\boldsymbol{_n}\large{\mathbf{\pi}}\boldsymbol{_r}=n^r}$$

◇　重複組合せ $${\boldsymbol{_n}\mathbf{H}\boldsymbol{_r}}$$
例：x＋y＋z＋w＝10 を満たす負でない整数解の個数は？
○○○｜○○○○｜○｜○○　←→　(x , y , z , w)＝(3 , 4 , 1 , 2)
｜｜○○○○○○○○○○｜　←→　(x , y , z , w)＝(0 , 0 , 10 , 0)
　　　　　　　　　　　　　　：
と考えれば 1：1 に対応するから、
○10個と棒3本を並べる場合の数を数えればよいことになる。
₄H₁₀ ＝ ₁₃C₁₀ ＝ ₁₃C₃ ＝ 286 個

　　一般に、
異なる n 個の中から重複を許して r 個取り出す（順番を区別しない）
　　　a　a　b　d・・・?
→　r 個の物を n 種類に分ける（規則正しく並べよう）
　　　　　　↓↑
→　r 個の○と n－1 本の棒を１列に並べる
　　　○○｜○｜｜○・・・○
→　$${\boldsymbol{_n}\mathbf{H}\boldsymbol{_r}=\boldsymbol{_{n+r-1}}\mathbf{C}\boldsymbol{_r}}$$

練習問題 【1】

サイコロを３回投げて出た目の数を順に a , b , c とする。次の確率は？
(1)　a , b , c がすべて異なる。 
(2)　a＜b＜c となる。
(3)　a≦b≦c となる。

《解説・解答》
すべての場合の数は、　　　　　　　₆π₃ ＝ 6³ ＝216通り
このうち、
(1)　a , b , c がすべて異なるのは、　₆P₃ ＝ 6•5•4 ＝120通り
(2)　a＜b＜c となるのは、　　　　  ₆C₃ ＝ 6•5•4／3•2•1 ＝20通り
(3)　a≦b≦c となるのは、　　　　　 ₆H₃ ＝ ₈C₃ ＝ 8•7•6／3•2•1 ＝56通り
以上から、
(1)　a , b , c がすべて異なる確率は、₆P₃／₆π₃ ＝120／216 ＝  5／9
(2)　a＜b＜c となる確率は、　　　  ₆C₃／₆π₃ ＝ 20／216 ＝ 5／54
(3)　a≦b≦c となる確率は、　　　　 ₆H₃／₆π₃ ＝ 56／216 ＝ 7／27

練習問題 【2】

1円玉、10円玉、100円玉が３枚ずつ、全部で９枚ある。この中から３枚とる。
(1)　異なる金額は全部で何通りある？
(2)　３枚の合計金額が111円になる確率はいくつ？

《解説・解答》
(1)　異なる３種類（1円玉、10円玉、100円玉）から重複を許して３個とって、取り出す順番を区別しないのだから、重複組合せ ₃H₃ にあたる。
　　₃H₃ ＝ ₅C₃ ＝ ₅C₂ ＝ 5•4／2•1 ＝10通り
※　全部書き出すと「3円、12円、21円、30円、102円、111円、120円、201円、210円、300円」の10通り。

(2)　すべての場合の数は、₉C₃ ＝ 9•8•7／3•2•1 ＝84通り（※）
　　また 1円玉、10円玉、100円玉のとり方はそれぞれ ₃C₁ ＝3通り だから、求める確率は 3•3•3／ ₉C₃ ＝ 9／28
※　このように「9枚のコインを全部区別して数える」ことで「同様に確からしい」が守られる。← 正しく確率計算するために必要なこと。

◇　　　　　　◇　　　　　　◇

〜 順列と組合せとその周辺 〜　
▷ 重複順列と重複組合せ　　　　　　　　
▷ パスカルの三角形の裏事情　　　　　　
▷ ３項定理とパスカルの四面体　　　　　
▷ 場合の数の数え方と確率の数え方の違い