
ゲーム理論のサンプル問題
ゲーム理論の問題を 同時ゲーム と 時間差ゲーム と 確率ゲーム の3種類に分けて解説しています。それぞれの「ゲームの解き方」は こちら をご覧ください。ここでは3種類のゲームのサンプルを示しています。
同時ゲームのサンプル問題
◇ 旅行の行き先をゲーム理論で解く
夫はミャンマーに行きたい。妻はフランスに行きたい。もちろん、2人で一緒に行きたい。さて、この夫婦の旅行の行き先はどうなるか?
夫と妻がミャンマーかフランスかのどちらかに行くとすると、その組み合わせは全部で4通りある。その4通りに優先順位をつけて1点~4点の得点を与えると、夫と妻の希望から4点と1点は下表のように決まる。
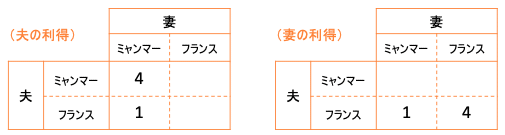
さて、問題は残り2つの選択肢だ。「自分の行きたいところに行く」のと「2人で一緒に旅行する」のとではどっちがいいか? どちらを優先するか?
(つまり、どちらの空欄に「3」を入れ、どちらの空欄に「2」を入れるか? そして、そのことで旅行の行き先がどう変わるか? という問題)
《ケース1》 2人とも「自分の行きたいところに行く」ことを優先する場合。
《ケース2》 2人とも「2人で一緒に行く」ことを優先する場合。
《ケース3》 夫が「2人で一緒に行く」ことを、妻が「自分の行きたいところに行く」ことを優先する場合。
《ケース4》 夫が「2人で一緒に行きたい」といい、妻が「別々がいい」という場合。
それぞれ「同時ゲームの解き方」に従って解いてみよう。
・ 人Aは、自分の利得を表の 上下 で比べて大きい方を選ぶ。
・ 人Bは、自分の利得を表の 左右 で比べて大きい方を選ぶ。
・ 両者の選択の重なったところがゲームの解。
《ケース1》 2人とも「自分の行きたいところに行く」ことを優先する場合。
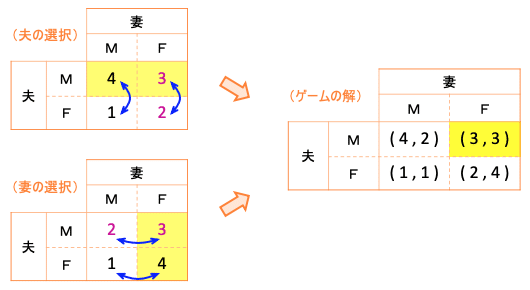
このケースでは、表の空欄には上のように2と3が入る。この場合、夫は妻の選択に関わらずミャンマーを選び、妻は夫の選択に関わらずフランスを選ぶ。その結果、夫はミャンマーへ、妻はフランスへと、別々に行くことになる。つまり、解は1つに決まる。
両者の利得(満足度)はどちらも3。二人とも少々不満が残る。
《ケース2》 2人とも「2人で一緒に行く」ことを優先する場合。
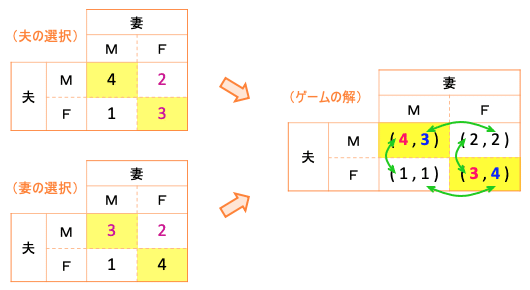
このケースでは、数 2 と 3 の場所が《ケース1》と逆転する。そして、ゲームの解も変わる。
夫の選択は妻の選択によって変わり、妻の選択は夫の選択によって変わる。二人の選択が重なる部分は2つある。すなわち、解は2つある。
二人で一緒に行くことにはなるのだが、行き先がミャンマーなのかフランスなのかが決まらない。
《ケース3》 夫が「2人で一緒に行く」ことを、妻が「自分の行きたいところに行く」ことを優先する場合。
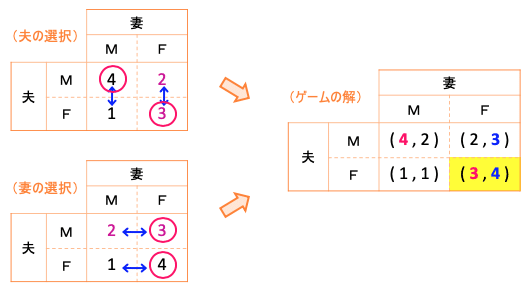
この場合は解が1つに決まる。妻が行きたいフランスに二人で一緒に行くことになる。妻にとってはフルマークの 4 点、夫にとっても納得の 3 点というところだろう。
けれども「わがまま言った方の勝ち?」みたいで、夫としては割り切れない部分も残る。二人の優先順位が変わらなければ、夫の希望は永遠に満たされそうにない。
《ケース4》 夫が「2人で一緒に行きたい」といい、妻が「別々がいい」という場合。
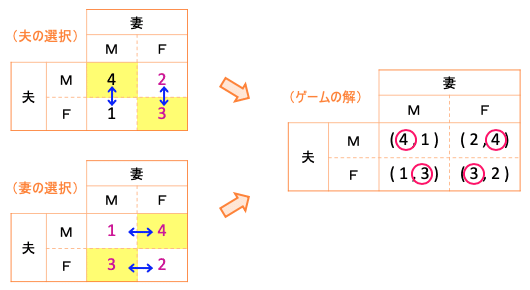
この場合は妻の優先順位(利得)が前の3つのケースとは変わっている。そしてこの場合、二人の選択には重なる部分が無い。つまり、このゲームには解が無い。妻がフランスに行きたいと言えば、夫もフランスに行くと言い、そうなると妻は行き先を変更し、夫も・・・とぐるぐる廻って、いつまでも安定しない。
ところで、《ケース1》と《ケース2》では二人の優先順位が同じだが、《ケース3》と《ケース4》はそうではない。前者のようなケースを「対称ゲーム」と、後者のようなケースを「非対称ゲーム」と呼んでもよかろう。
さて、《ケース1》と《ケース3》では解が1つに決まったが、《ケース2》と《ケース4》ではそうではなかった。以上のことは、これらを「同時ゲーム」ととらえたときの解である。ところで、これらを「時間差ゲーム」ととらえると解は違ってくる。そのことはまた後で、別の問題として考える。
なお、《ケース4》はゲーム理論のおもしろいテーマになる。実はこれ、サッカーのPK戦と同じなのだ。キッカーが蹴るのと同じ方向に飛ぼうとするゴール・キーパーは「一緒に行きたい」という夫と同じ立場で、ゴール・キーパーの裏をかきたいキッカーは「別々がいい」という妻と同じ立場なのだ。まさにサッカーというゲームの中で合理的な判断とはどのようなものかを考える格好のテーマなのだ。これについてはまた後で「確率ゲーム」として考える。
時間差ゲームのサンプル問題
<例1> 時間差ゲームは後ろから順に考える。
先手の立場で、後手が打つ手を考える。(時間さかのぼり法)
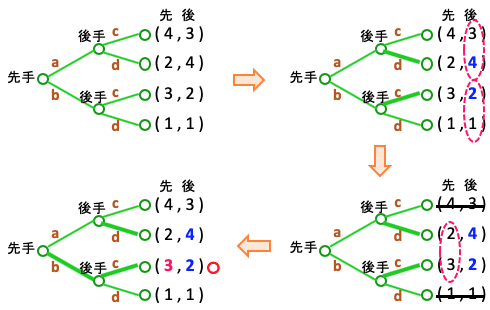
後手は最後の分岐で自分の利得が大きい方を選ぶ。この時点で (4 , 3) と (1 , 1) の可能性は消える。
先手は後残った2つの枝のうち自分の利得が大きい方を選ぶ。すなわち先手,後手の打つ手は (b , c) で、そのときの利得は (3 , 2) となる。これがゲームの解。
※ 合計の値で見ると (4 , 3) の方が良さそうだが、先手が戦略 a をとった場合は後手は戦略 d を取った方が利得が大きいので、結果として先手の利得は 2 になってしまう。
<例2> はやや複雑系だが、後ろから考えるという手順は <例1> と同じ。BはCの手を読み、AはBとCの手を読む。Cは自分のことだけを考えれば十分。
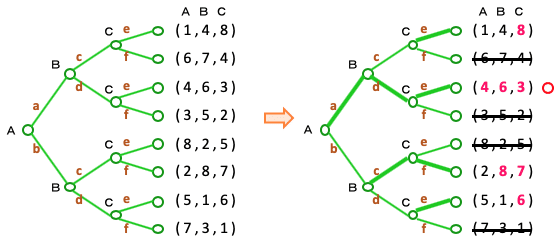
まず C の打つ手を考える。最後の4ヶ所の分岐のそれぞれで C は2数を比べて大きい方を選ぶ。この時点で4つの可能性が消え、候補は4つに絞られる。
次に B の打つ手を考える。4つの候補のうち2つずつを比べて大きい方を選ぶ。この時点で候補は (4 , 6 , 3) と (2 , 8 , 7) の2つに絞られる。
A はその2つを比べて、自分自身の利得の大きい方を選ぶ。すなわち A , B , C の手は (a , d , e) で、そのときの利得は (4 , 6 , 3) となる。これがゲームの解。
◇ ジャンケンの解
ジャンケンをしたとき、勝ちの利得を +1、あいこの利得を 0、負けの利得を -1 とする。ジャンケンを同時ゲームと時間差ゲームの2つで解いてみよう。
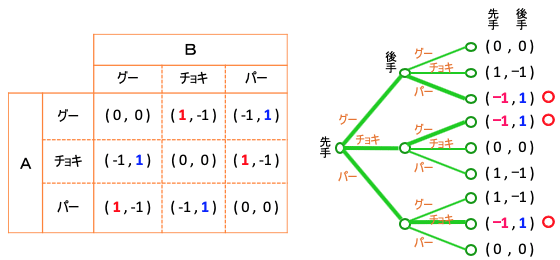
同時ゲーム(上左表)では A の選択と B の選択が重ならない。つまり、解は無い。
一方、時間差ゲーム(上右図)には3つの解がある。「先手必敗、後手必勝」である。
「同時ジャンケンはなぜ役立つのか?」というと「解が無い」からだ。「後出しジャンケンはなぜズルなのか?」というと「解がある」からだ。解があればいいというものではないのである。(と、◯◯先生に言ってあげてください)
確率ゲームのサンプル問題
◇ サッカーのPK戦をゲーム理論で解く
次表はキッカーが左右のどちらかに蹴り、キーパーが左右のどちらかに飛んだときのゴール決定率である。 キッカーがゴール決定率を高めるためには、またキーパーがゴール阻止率を高めるためにはそれぞれどのような戦略を立てればいいだろうか?
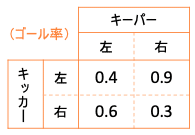
キッカーが蹴る方向をキーパーに読まれたらゴール決定率は下がる。 キーパーが飛ぶ方向をキッカーに読まれたらゴール阻止率は下がる。 だから、キッカーは蹴る方向を、キーパーは飛ぶ方向をそれぞれ確率的に決めた方がいい。
さて問題は、キッカーはどういう確率で蹴ればいいか、キーパーはどういう確率で飛べばいいかだ。 それぞれにとって最適な比率が各自の採るべき戦略であり、両者がその戦略を採ったときのゴール率がゲームの解である。
《キーパーの立場で最善策を考える》
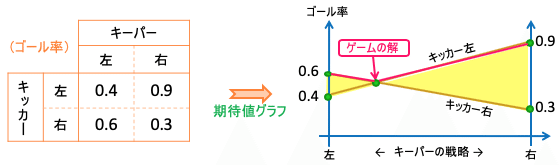
2本の直線はキッカーが左に蹴った場合と右に蹴った場合のゴール率(期待値)のグラフ。
さて、キッカーがどっち蹴ろうがキーパーがどっちに飛ぼうが、ゴール率は必ず図の黄色の範囲に収まる。また、キッカーはゴール率を上げたいのだから、キッカーが合理的であればゴール率はその下限(赤線の部分)になる。
そう考えると、上の2直線の交点がキーパーにとっての最善策ということになる。
《キッカーの立場で最善策を考える》
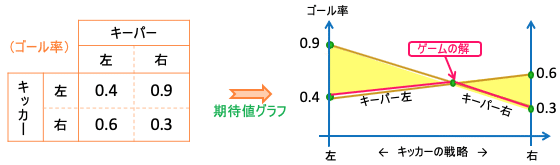
キッカーの立場で考えても同じ。キッカーがどっちにどんな割合で蹴ろうが、キーパーがどっちにどんな割合で飛ぼうが、ゴール率は図の黄色の範囲に収まり、キーパーが合理的ならその下限(赤線部分)になる。 だから、キッカーにとっては上の2直線の交点が最も好ましいことになる。
キッカー・キーパーにとっての最善策、ならびにそのときのゴール率を求めるには、上のグラフから相似比を使えばよい。
《拡張版利得表》
ところで、相似比は辺の長さの比であり、この場合は利得表の数の差である。また、相似比の逆比がキッカー・キーパーの採るべき戦略に、その比でゴール率の加重平均を取った値がそのときのゴール率になる。
だから、下のように利得表の下と右に欄を付け足して数を書き込めばゲームの解が求められる。これが、確率ゲームを解くための安直法である。
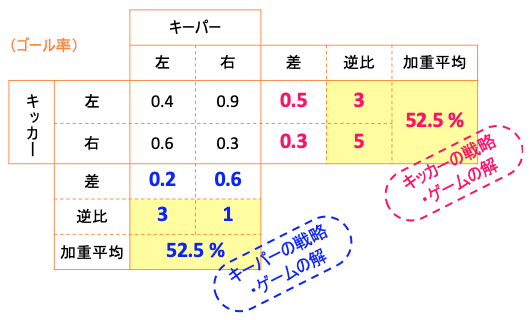
以上から、キッカーは左右に 3:5 の比で蹴り分け、キーパーは左右に 3:1 の比で飛び分けるのがそれぞれの最善策であり、双方がその戦略を採った場合のゴール率は 52.5 % である。
◇ ◇ ◇
〜 ゲーム理論 練習帳 〜
▷ ゲームの解き方
▷ サンプル問題
▷ ゲームを変える + 社会的ジレンマの数々 + ベストな配分を探れ
