
結論を言わない証明問題
証明問題といえば、「○○が成り立つことを証明せよ」というのが一般的な出題の形です。つまり、設問の中に結論「○○」を書いちゃうわけです。でも、「成り立つ」のが分かっているのを証明するのって、つまらなくないですか? 「成り立つ」と言い切っちゃって、生徒の楽しみを奪ってませんか? 「仮説→検証」が科学的態度。数学者だって「予想→証明」に人生をかける。それなのに、出題者が結論を言っちゃっていいんですか?
結論を書いた上で「さぁ証明しろ」だなんて、生徒の側からすれば、それは仮説でもなければ予想でもありません。それは絶対に正しいものです。そうでなければ、出題ミスということになってしまいますから。疑う気持ちが微塵も無い中で証明するのって、モチベーションとしておかしくないですか? 正しいかどうかわからないからこそ、証明する必然性があるんじゃないんですか?
そう考えて、私は結論(またはその一部)を空欄にして出題してみました。生徒たちに、まず予想を立てて、続いて自らそれを証明してもらおうというわけです。もちろん空欄に入るものは一意に決まるように作ってあります。そうすると、がぜん正答率が下がるのです。ものによっては、ボロボロになります。
でも、そうすることで「仮説・予想を立てる」という数学の最も楽しい部分を生徒たちに経験させられます。そしてそれが証明できれば、そこに至ってようやく彼らはそれが正しいことを確信します。証明問題は本来こうあるべきだろうと私は思うのです。
これから5題取り上げます。いずれも中学・高校の幾何の範囲からの出題です。
合同な三角形を探せ
【1】下図において △ABC と △CDE はどちらも正三角形である。
このとき、△___ ≡ △___ が成り立つ。
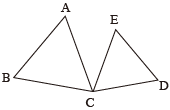
中学1年で学ぶ「三角形の合同」の証明問題です。どの問題集にも必ずと言っていいほど載っている典型的な問題です。でも、普通は設問の中に結論がズバリ書いてあります。上ではそこを空欄にして、まず合同な三角形を探して、続いてそれを証明してもらおうというわけです。
さて、合同な三角形を探すとなると、補助線を引かなければなりません。ところで、結論が書いてある場合はあらかじめ補助線が引いてあるのと同じことですから、補助線を引くという試行錯誤の過程も無くなっているわけです。
それに対してこの場合は、補助線をあちこち引いてみて、まず合同に見える三角形を探すことになるでしょう。そして見つかったとしてもそれは予想にすぎませんから、回答者はすぐには確信を持てないでしょう。そして「本当に合同になるのかな?」と思いながら、確認しようとするでしょう。この心の動きこそが数学の楽しみだと私は思うのですが、いかがでしょうか。
※ 【1】の解答は こちら をどうぞ。
同一円周上にある4点を探せ
【2】下図で2円は点 P で接し、PQ は2円の接線である。
このとき、4点 ________ は同一円周上にある。
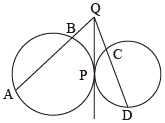
次は、まず同一円周上にある4点を探して、それを証明する問題です。では、探してみましょう。まず「B , P , C , Q の4点が同一円周上にある…(1)」ように見えるでしょうか。でも残念ながら、その4点は同一円周上にはありません。
他に探してみると、「A , B , C , D の4点が同一円周上にある…(2)」ように見えるでしょうか。実は、それが正解です。
ところで、この問題を生徒にやらせてみたところ、空欄に (1) を入れた生徒が一定数いました。もちろん (1) は成り立たないので証明できるはずがないのですが、それっぽい証明みたいなものを書いてくるんですね。そしておそらくはそんな解答を書いた生徒たちの中にも、正しい結論 (2) を書いた形で問題を出せば正しい証明を書く生徒も一定数いることでしょう。つまり、結論が書いてある問題で正しい証明が書けたとしても、その人が本当にちゃんと分かっているかどうかは疑わしいと私は思うのです。
※ 【2】の解答は こちら をどうぞ。
合同か?
【3】円に内接する四角形 ABCD がある。
対角線 AC と BD の交点を E とする。
AC=BD のとき、△ABE≡△DCE は成り立つか?
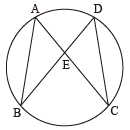
この問題では「△ABE≡△DCE が成り立つ」とは言っていません。「成り立つか?」という言い方がポイントです。この問題の趣旨は「成り立つというなら、証明してね。成り立たないというなら、反例を挙げてね」ということです。
さて、どうでしょうか。まず三角形の角度が等しいことはすぐに分かりますから、△ABEと△DCEが相似であることは分かります。ですから「三角形のどこかの辺の長さが等しい」ことが分かれば、△ABE≡△DCE と言えます。さて、どの辺の長さが等しいと言えるでしょうか。それをどうやったら言えるでしょうか。
この問題を中学2年の授業でやってみました。そうしたらある生徒が「出来ました!」と言うものだから、見せてもらいました。そして「この部分、絶対成り立つかな? この部分、詰めが甘くないか?」、そんな言い方をして突き返しました。そうすると別の生徒が「出来ました!」、また別の生徒が「今度こそ絶対!」と言って私に見せにくるものだから、しばらくすると長い行列ができました。
私は言いました。「証明できちゃったのか、それは残念だったね。みんなバツだよ。だって『成り立たない』んだもん。オレ反例知ってるし」。そうすると今度は生徒たちは反例を探し始めるのですが、闇雲に探しても見つからないんですね。むしろ合同を証明するつもりで、丁寧に「これは絶対成り立つか? 他の可能性はないか?」と考えることで、他の可能性=反例が見えてくるのです。
例えば、ありがちな間違いは「AC=BD より ∠ABC=∠DCB」とやっちゃうことですが、「等しい弧に対する円周角は等しい」は成り立っても、「等しい弦に対する円周角は等しい」は成り立ちませんね。弦を1つ決めても円周角は2つあるからです。そしてこのことを詰めて考えれば、反例が見えてくるでしょう。
あるいは「AB と CD の交点を F とする」とやると、それはそれでなんとか証明みたいなものが出来上がります。けれども「そもそも AB と CD は交わるのか?」と考えると、やっぱり反例が見えてくるでしょう。
他に「方べきの定理」を使う方法もありますが、雑にやると合同の証明みたいになっちゃいますが、丁寧にやるとそこからも反例が見えてくるでしょう。
反例が見えてしまえば、きっと「なるほど」と思っていただけるでしょう。お試しください。
※ 【3】の解答は こちら をどうぞ。
角の2等分線を3本引くと...
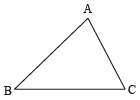
【4】 二等辺三角形でない△ABC がある。
∠A の内角の二等分線と直線 BC の交点を D 、
∠B の内角の二等分線と直線 CA の交点を E 、
∠C の内角の二等分線と直線 AB の交点を F とする。
このとき ______________________________ 。
この問題も結論を伏せています。回答者にまず結論を答えてもらって、続いて証明してもらおうというのがこの問題の趣旨です。
さて、この問題なら結論を知っている人は多いでしょう。結論は「3直線 AD , BE , CF は1点で交わる」です。その点を「内心」と呼ぶことを知っている人も多いでしょう。
では、次の問題はどうでしょうか。
【4’】 二等辺三角形でない△ABC がある。
∠A の外角の二等分線と直線 BC の交点を D 、
∠B の外角の二等分線と直線 CA の交点を E 、
∠C の外角の二等分線と直線 AB の交点を F とする。
このとき ______________________________ 。
問題【4】の「内角」を3か所、「外角」に変えたものが問題【4’】です。違うのはそこだけですが、こうなると結論を知らない人が多いでしょう。そしてこうなると、まず結論を予想して、でも確信は持てないでしょうから、きちんと証明したくなることでしょう。こちらの問題が本題です。
ところで私が授業で扱ったときはプリントに【4】を載せておいて、生徒たちが「楽勝だよ」と思ったところで、「あっしまった、ミスプリ発見! 『内角』じゃなくて、『外角』だった。『内角』を『外角』に書き換えてやってくれ」と言いました。下手な演技をしているわけですが、生徒たちにとっては楽勝どころか、急に難問になるんですね。
というのは、この問題はなかなか予想も立たないのです。図を雑に描いたら、まず無理でしょう。3点 D , E , F は三角形の外側のだいぶ遠いところにきますから、コツは紙の真ん中あたりに小さめに、かつ鈍角三角形を描くことです。その上で角度はかなり正確に2等分して、まっすぐの直線を引きましょう。そうするとなんとか予想が立つでしょう。でもそれはあくまでも予想ですから、回答者にとって納得というわけにはいきませんね。どんな三角形でも成り立つことを確認するには、やっぱり証明するしかないですね。
ところで【4】と【4’】の証明はほとんど同じと言えば、ほとんど同じなんです。「角の2等分線の公式」がありますが、内角を2等分する場合も外角を2等分する場合も成り立つ式はそっくりです。まずはじめにその公式を使って、そのあとの展開も【4】と【4’】の証明はそっくりなんです。そして最後だけが全然違う。両者を比較すると、平面幾何の理解が深まります。
※ 【4】の解答は こちら を、【4’】の解答は こちら をどうぞ。
四角形の頂点からの距離の和が最大になる点
【5】四角形ABCDにおいて、頂点 A , B , C , D からの距離の和
PA+PB+PC+PD が最小になるような点 P はどこにあるか?
まず予想してみてください。おそらく多くの人は「対角線 AC と BD の交点…(3)」と予想するのではないでしょうか。私もそう予想しました。さて、合っているでしょうか。
《図1》において、対角線 AC と BD の交点を P として、点 P と異なる位置に P' をとると、「PA+PB+PC+PD<P'A+P'B+P'C+P'D」となります。その訳は端的に言えば、「遠回りするより直線で進んだ方が近い」からです。というわけで、《図1》において (3) が証明できます。
でも、どんな四角形でも (3) が言えるでしょうか。
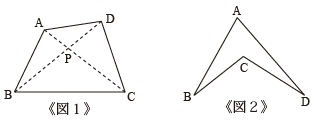
《図2》の四角形ではどうでしょうか。この場合は「対角線 AC と BD の交点」よりも PA+PB+PC+PD の値がもっと小さくなる点がありそうですね。ここでも予想を立てましょう。《図2》の場合、みなさんはどのように予想しますか。
おそらく多くの人は「点 C」と予想するのではないでしょうか。私もそう予想しました。けれども、私には証明できないのです。《図1》では予想が当たっていました。証明もできました。けれども《図2》では予想は立つけれど、証明できないのです。ですから、私に確信はありません。というより、頑張っても証明できないということは、予想が間違っているかもしれません。
というわけで、問題【5】は私には分かりません。でも、いいじゃないですか。この発表のタイトルが「結論を言わない証明問題」ですから、その趣旨を踏まえて「結論が分からない証明問題」もあってよろしいんじゃないでしょうか。本当に私には分からないので、どなたか解決できた方がいらっしゃいましたら、ぜひ教えてくださいませ。
※ 【5】《図1》の証明は こちら をどうぞ。
結論を言っちゃったら、回答者に疑いの気持ちが微塵も無くなっちゃう。それは絶対に正しいものです。そうじゃなかったら、出題ミスってことになっちゃいますから。でも、成り立つことがわかっているものを証明するのって、つまらなくないですか? モチベーションとして不自然じゃないですか?
結論を言っちゃったら、検証というより作業になっちゃいます。そしてそうなると、よく分からなくてもそれっぽく書けちゃうんですね。見つける楽しさ、見つけたときの驚きはどこ行った?
では、どうすれば良いか。単純な話です。結論を言わなければ良いんです。それだけで、証明問題が楽しくなります。出題者は極力結論を言わないように心掛けてくださいね。
◇ ◇ ◇
〜 私の数学教育論 〜
▷ 結論を言わない証明問題 + 解答編
▷ 数学屋が売れる時代になってきた
▷ 「3」のマジック
〜 考えるための数学問題集 〜
▷ わかれば瞬殺、答えを見れば一目瞭然
▷ ピタゴラス数は3,4,5の倍数から成る
▷ 相似な図形
▷ 「鳩の巣原理」で考えてみよう
▷ 結論を言わない証明問題
