だまされやすい確率

【3】１組のトランプの絵札（ジャック、クイーン、キング）の合計12枚の中から任意に4枚の札を選ぶとき、ジャック、クイーン、キングの札がそれぞれ少なくとも1枚選ばれる確率を求めよ。　　　（北海学園大 2002年）
　　・・・という問題に対して、Ａ君、Ｂ君、Ｃ君は次のように答えた。正しいのは、だれ？

　　　　《Ａ君の答え》
総数（分母）は $${_{12} \textup{C}_4}$$ 通り。
分子は、まずＪ,Ｑ,Ｋの決め方が $${4^3}$$ 通り。残り９枚の中から任意の１枚をとる。
よって、求める確率は  $${\dfrac{4^3 \times 9}{_{12} \textup{C}_4}}$$

　　　　《Ｂ君の答え》
まず３枚とり出して、その中にＪ,Ｑ,Ｋが含まれる確率は  $${\dfrac{4^3}{_{12} \textup{C}_3}}$$
次に、残り9枚の中から任意の1枚をとる。
よって、求める確率は  $${\dfrac{4^3}{_{12} \textup{C}_3} \times \dfrac{9}{9}}$$

　　　　《Ｃ君の答え》
余事象を考える。Ｊ,Ｑだけが出るのは $${_{8} \textup{C}_4}$$ 通り。
Ｑ,Ｋだけが出る場合も、Ｋ,Ｊだけが出る場合も同じ。
よって、求める確率は　$${1-\dfrac{_{8} \textup{C}_4 \times 3}{_{12} \textup{C}_4}}$$

　生徒たちから「Ａ君じゃね？」「いや、Ｃ君だ」「全部合ってるように思う」などいろんな声が出たが、実はＡ君,Ｂ君,Ｃ君ともみんな間違い。（おぃおぃそれくらい気づけよ！）
　そこで私は「じゃぁ正しい確率出してよ」と振る。生徒たちは再び考え始めて、途中で他の人のと見比べると・・・合わない。みんなが出している数値が何パターンもあって、どれが正解だかわからない。
　ほぅれみろ。確率って出来そうで出来ないだろ。それを実感してもらうためにこの問題をやってるのさ。確率の問題って、解説を聞いたり答えを見たりすれば「ふむふむ」と分かった気になる。でも自分でやろうとすると、合わない。そういうもんなのさ。だからさ、僕が間違った答えを言っても、君らはたぶん信じるよ。僕はね、ここにいる全員をだます自信があるよ。
　そこで、まずは「Ａ君、Ｂ君、Ｃ君の答え方、どこが間違っているのか指摘して」みよう。そうじゃないと、だまされる。Ａ君、Ｂ君、Ｃ君がどこで間違ったかというと、結局はモレがあったり、ダブったりということだ。

・Ａ君は、たとえば「（J1，Q1，K1）＋（J2）と（J2，Q1，K1）＋（J1）」をダブって数えている。
・Ｂ君は、たとえば「初めに（Ｊ，Ｊ，Ｑ）を取り出して、最後に（Ｋ）を取り出す場合」がモレている。
・Ｃ君は、たとえば「Ｊだけが出る場合」を２回ダブってカウントして、余計に引いている。

　では、ここで【3】の正しい答えを言おう。Ａ君、Ｂ君、Ｃ君の答え方を修正してもできるのだろうけれど、僕は次のように数えた。

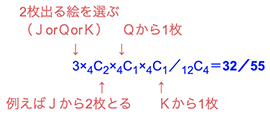
2枚出る絵を選ぶ
（ＪorＱorＫ）　　Ｑから1枚
　　　↓　　　　　　↓
　　　$${3 \times _{4} \textup{C}_2 \times _{4} \textup{C}_1 \times _{4} \textup{C}_1 \div  _{12} \textup{C}_4 = \dfrac{32}{55}}$$
　　　　　　↑　　　　　　　↑　
　例えばＪから2枚とる　　Ｋから1枚

　ここで生徒たちは「なるほど」という顔をする。僕はすかさず「ほぅら、まただまされた！」。でも実はこれが正解。でも、そんなことは口が裂けても言わない。

◇　　　　　　◇　　　　　　◇

〜 確率名人への道 〜　
【1】 場合の数の数え方 と 確率の数え方 の違い
【2】 ひもを結ぶ問題　　　　　　　　　　　　
【3】 だまされやすい確率　　　　　　　　　　
【4】 気づきにくいダブりとモレ　　　　　　　
【5】 数学でアクティブ・ラーニング例