
直交座標系シャワー と 極座標系シャワー
直交座標系シャワー と 極座標系シャワー
2018年春、ベトナムを旅行中に、シャワーには2種類あることに気がつきました。ベトナムのシャワーは「直交座標系」で、ウチのシャワーは「極座標系」。
直交座標系のシャワーは、温度と流量を調整するのに手間がかかる。熱すぎては困るので、まず水の方から回す。そうすると「ぬるっ → あつっ → チョロチョロ → ぬるっ → ドバーッ → あつっ → …」となりがちで、一旦シャワーを止めると、また一からやり直し。
一方、極座標系のシャワーは、まず温度を決めて、次に流量を決めれば良いので、素早くピタッと快適な温度・流量になります。
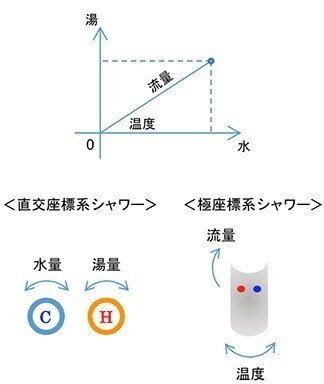
シャワーは極座標系に限る。
ボールを遠くに投げるための角度
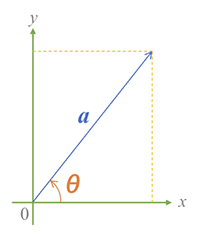
【問】変数 t が正の値をとって変わるとき、
点 P(a cosθ・t , a sinθ・t-b t² )について考える。
ただし、a と θ は定数で、a>0 ,b>0 ,0°<θ<90° である。
(1) 点 P の軌跡を求めよ。
(2) 点 P の y 座標が 0 になるときの点 P の x 座標を求めよ。
(3) (2) の x 座標の値が最大になるのは、定数 θ がいくつのときか。
《 答え 》
(1) x= a cosθ・t …① , y=a sinθ・t-b t² …② とおく。
①より t=x/a cosθ
これを②に代入して y=x tanθ-b x² /a² cos² θ(x>0)
└→ 放物線軌道を描く
(2) y=a sinθ・t-b t² =t(a sinθ-b t)=0 より t=a/b sinθ(∵t>0)
このとき x=acosθ・t= a²/b sinθcosθ= a²/b sin2θ/2
(3) (2)より x が最大になるのは 2θ=90° ⇔ θ=45°のとき。
以上から、ボールを遠くに投げるには仰角45°の角度で投げれば良いことがわかる。つまり、初速 a ,重力加速度 b に影響されない。とはいえ、現実には空気の影響(空気抵抗)は受ける。
◇ ◇ ◇
〜 授業の数学 〜
▷ 直交座標系シャワー と 極座標系シャワー
▷ 私はあなたをiしています ▷ 京大入試・数学2010
▷ すべて と 少なくとも ▷ みんなでワイワイ軌跡の問題
