ベストな配分を探れ

　ゲーム理論の確率ゲームを２問。ゲームの解き方マニュアルはこちら（→ 確率ゲームと期待値グラフ ）を、サンプルはこちら（→ サッカーのＰＫ戦 ）をご覧ください。

◇　ピッチャーは直球と変化球を投げ分けます。バッターはどちらが来るかを予想して打ちます。次表はピッチャーの配球とバッターの予想の組み合わせ別のバッターの打率です。
　さて、バッターをアウトにしたいピッチャーは直球と変化球をどのような割合で投げ分けたらいいでしょうか。ヒットを打ちたいバッターは直球・変化球のどちらが来るかをどのような割合で予想したらいいでしょうか。また、両者がそれぞれその割合で配球・予想して対決した場合、バッターがヒットを打つ確率（長い目で見れば、この値がバッターの打率になります）はいくらになるでしょうか。ただし、ピッチャーはストライクだけを投げ、バッターは必ずフェア・グラウンドに打ち返すものとします。

◇　Ａ君とＢ君がグー・パーだけを出してじゃんけんする。チョキは出さない。そしてこのとき、次のように勝ち負けが決まる。
　　○　両者が同じ手を出したときはＢ君の勝ち。
　　　　グー・グーなら１点、パー・パーなら６点をＢ君が得る。
　　○　両者が違う手を出したときはＡ君の勝ち。
　　　　このときＡ君は３点を得る。
　さて、この勝負、Ａ君とＢ君ではどちらが有利だろうか？
(1)　Ａ君もＢ君もグーとパーを同じ割合（1/2ずつ）で出す場合。
(2)　Ａ君とＢ君が自分に有利になるようにグー・パーの配分を変えた場合。

　《解説・解答》は以下をどうぞ。

ピッチャーの配球 VS バッターの予想

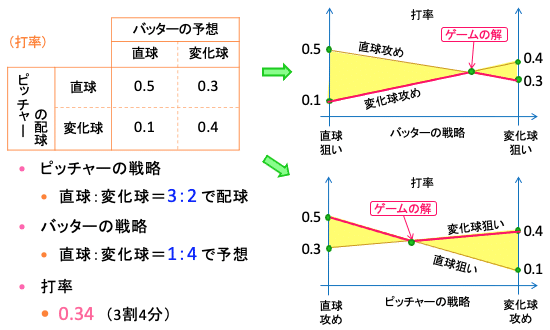
　期待値グラフ（↑）を描いて２直線の交点から求めることもできるが、拡張版利得表（↓）からゲームの解を求める方が楽だろう。

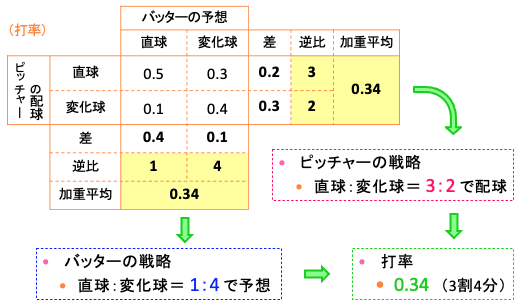
◇　ピッチャーの戦略　　直球：変化球＝ 3：2 で配球
◇　バッターの戦略　　　直球：変化球＝ 1：4 で予想
◇　ゲームの解　　　　　打率は 0.34（3割4分）

　結果からみると、ピッチャーは打たれやすい直球を多めに投げた方がよくて、バッターは苦手な変化球を多めに予測した方がよいということになる。ピッチャーもバッターもよい成績を残すためには、得意な方をさらに磨くより、苦手を克服するべきだということなのだろうか？

グーパーじゃんけんで勝負する

　Ａ君の立場で利得表を作ると次のようになる。

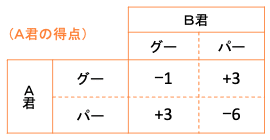
(1)　Ａ君もＢ君もグーとパーを同じ割合（1/2ずつ）で出す場合。

　(1)は普通の数学の問題。かなり簡単め。Ａ君の期待値は、

1/2×1/2×(-1) ＋ 1/2×1/2×3 ＋ 1/2×1/2×3 ＋ 1/2×1/2×(-6)＝−1/4＜0
　　↑　　　　　　↑　　　　　　↑　　　　　　↑
グー・グー　　グー・パー　　パー・グー　　パー・パー

　Ａ君の期待値がマイナスになるから、Ａ君は不利。つまり、Ｂ君が有利。

(2)　Ａ君とＢ君が自分に有利になるようにグー・パーの配分を変えた場合。

　(2)はゲーム理論（確率ゲーム）の問題。拡張版利得表を書くと、

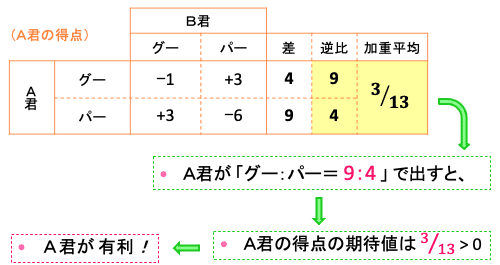
となる。表より、Ａ君が「グー：パー＝9：4」の割合で出すと、Ａ君の得点の期待値は 3／13＞0 となる。よって、Ａ君が有利！という結果になる。
　Ｂ君がグーを出す確率を p 、パーを出す確率を 1−p として計算してみると、Ａ君の期待値は、

9/13×p×(-1)＋9/13×(1−p)×3＋4/13×p×3＋4/13×(1−p)×(-6)＝3/13

見ての通り、p が消えて、期待値は先ほどと同じく 3／13 となった。結局Ｂ君がグー・パーをどんな割合で出しても、Ａ君有利は変わらないのです。

◇　　　　　　◇　　　　　　◇

　　　　　　　　　〜 ゲーム理論 練習帳 〜
　　▷ ゲームの解き方
　　▷ サンプル問題
　　▷ ゲームを変える ＋ 社会的ジレンマの数々 ＋ ベストな配分を探れ