
n枚のカード問題
◯ 1枚のカード問題
カードが1枚あって、片面に数字の 9 が書いてあり、もう片方の面にも1つの自然数が書いてあります。
「奇数の裏面は素数」(奇数が書かれている面の反対の面には素数が書かれている)が正しいとすると、9 の反対の面に書かれている数字は何ですか?
$${\begin{array}{|c|} \hline 9 \\ \hline\end{array}}$$
◯ 3枚のカード問題
両面が白のカードが1枚、両面が黒のカードが1枚、片面が白で片面が黒のカードが1枚、全部で3枚のカードがあります。
袋の中から1枚を選んでテーブルの上に置いたら、上面は白でした。そのカードをめくったとき、下面が白である確率はいくつですか?
◯ 4枚のカード問題
4枚のカードがあって、片面には数字1つが、もう片面にはアルファベット1文字が書いてあります。ある情報筋によると「偶数の裏は母音である」という話です。
なるべく少ない枚数のカードをめくって「偶数の裏は母音である」がホントかウソか(真か偽か)を確かめるには、どのカードをめくればいいでしょうか?
$${\begin{array}{|c|} \hline 3 \\ \hline\end{array}}$$ $${\begin{array}{|c|} \hline 6 \\ \hline\end{array}}$$ $${\begin{array}{|c|} \hline T \\ \hline\end{array}}$$ $${\begin{array}{|c|} \hline A \\ \hline\end{array}}$$

そそうに答えると間違えますよ。では、《解説・解答》と行きましょう。
1枚のカード問題
カードが1枚あって、片面に数字の 9 が書いてあり、もう片方の面にも1つの自然数が書いてあります。
「奇数の裏面は素数」(奇数が書かれている面の反対の面には素数が書かれている)が正しいとすると、9 の反対の面に書かれている数字は何ですか?
$${\begin{array}{|c|} \hline 9 \\ \hline\end{array}}$$
《解説》
9 は奇数だから、条件「片面が奇数 ⇒ その裏面は素数」より、9 の裏面は素数である。… ①
次に、対偶を考える。対偶「片面が素数でない ⇒ その裏面は偶数」である。
9 は素数でないし、「元の条件が正しい ⇔ 対偶も正しい」から、9 の裏面は偶数である。… ②
① , ②より、9 の裏面に書かれている数は「素数であり かつ 偶数である数」である。
そのような数は1つしかない。
①は納得できるが、②は納得できないという人のために、X に適当な数を入れて試してみよう。
X=3 の場合、「9 の裏が 3」は条件「奇数の裏面は素数」に合うようにみえるが、表と裏を入れ替えてみると「3(奇数)の裏が 9(素数でない)」となって、条件に合わない。
X=2 の場合、「9 の裏が 2」は条件「奇数の裏面は素数」を満たすし、表と裏を入れ替えて「2 の裏が 9」としても条件「奇数の裏面は素数」に矛盾しない。
つまり、正しい。
《答え》 2
3枚のカード問題
両面が白のカードが1枚、両面が黒のカードが1枚、片面が白で片面が黒のカードが1枚、全部で3枚のカードがあります。
袋の中から1枚を選んでテーブルの上に置いたら、上面は白でした。そのカードをめくったとき、下面が白である確率はいくつですか?
条件付き確率の問題ですが、確率の問題の中で統計の発想に近いのはこの手の問題です。
さて、上の問題を複数の人に答えてもらうと、大体3つの答えに分かれます。
《A君の答え》
上面が白で下面も白となるのは、両面が白のカードを取った場合だけ。つまり3枚のうちの1枚だから、求める確率は「1/3」である。
《B君の答え》
上面が白になるのは、白白のカードと白黒のカードの場合で、このうち裏返しても白なのは白白のカードだけ。よって、求める確率は「1/2」である。
《C君の答え》
カードの選び方が3通り、どちらを上にして置くかで2通り、全部で6通りと考える。
上 : 白1 白2 黒1 黒2 白3 黒3
下 : 白2 白1 黒2 黒1 黒3 白3
上が白: ◯ ◯ ◯
下も白: ◯ ◯
このうち上面が白であるのは3通り。この3通りのうち、下面が白であるのは2通り。よって、求める確率は「2/3」である。
さて、正しいのはどれでしょうか。あるいはどれも間違っているのでしょうか。
実際にやってみるとどうなるでしょうか。でも、確率的に現れる現象には必然的にバラツキが伴いますから、10回や20回じゃまるで足りない。実際にやって確信を得るには、少なくとも100回、できることならさらに多くの回数やった方が良いでしょう。ちょっと気が遠くなるでしょうか。
シンプルなのに、意外と難しい問題でしょ。でも、これこそが統計のセンスを養う問題だろうと思います。正解はC君の「2/3」です。
4枚のカード問題
4枚のカードがあって、片面には数字1つが、もう片面にはアルファベット1文字が書いてあります。ある情報筋によると「偶数の裏は母音である」という話です。
なるべく少ない枚数のカードをめくって「偶数の裏は母音である」がホントかウソか(真か偽か)を確かめるには、どのカードをめくればいいでしょうか?
$${\begin{array}{|c|} \hline 3 \\ \hline\end{array}}$$ $${\begin{array}{|c|} \hline 6 \\ \hline\end{array}}$$ $${\begin{array}{|c|} \hline T \\ \hline\end{array}}$$ $${\begin{array}{|c|} \hline A \\ \hline\end{array}}$$

《解説》
P:カードの片面が偶数 Q:カードの片面が母音 とする。
「偶数の裏は母音である」を論理式で書くと「P ⇒ Q」となる。
さて、「P ⇒ Q」の真理値は下表のようになる。
(表の 1 は 真 を、0 は 偽 を表す)
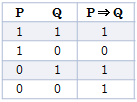
表で「P ⇒ Q」の欄が 0 になっているのは表の2行目だけだから、P が 真 のときと Q が 偽 のときだけを調べれば十分である。
P が 真 のときというのは「片面が偶数」のときだから、「6」のカードにあたる。
Q が 偽 のときというのは「片面が子音」のときだから、「T」のカードにあたる。
「偶数の裏は母音である」がウソといえるのは、「6」の裏が子音のときか「T」の裏が偶数のときだけである。
以上の説明で十分なはずだが、念のため「3」と「A」のカードについても確認してみよう。
「3」は奇数 すなわち P=0 だから、表の3行目と4行目をみると「P ⇒ Q」はどちらも 1 。
「A」は母音 すなわち Q=1 だから、表の1行目と3行目をみると「P ⇒ Q」はどちらも 1 。
つまり「3」と「A」のカードは、めくって何が出ても「偶数の裏は母音」の正しさは揺らがない。
まだ信じない人のために、試しに「A」のカードをめくってみることを考えよう。
もし「A」の裏面が偶数だったら、「偶数の裏が母音」だということになり文句なく正しい。
もし奇数なら「奇数の裏が母音」ということになるが、「偶数の裏は母音」が間違っていることにはならない。
結局のところ、「A」をめくって何が出ても「偶数の裏は母音」は正しい。
だから、めくっても無駄なのだ。
《 答え 》
「6」と「T」の2枚のカードをめくればよい。
◇ ◇ ◇
〜 論理クイズ 〜
▷ n枚のカード問題
▷ 天使か悪魔か妖精か
▷ 帽子は何色?
