
Python で埃をシミュレーションする
埃は部屋の隅にたまるものです。部屋の中ほどにも埃はいくらか積りますが、部屋の隅の方が多いですね。
ところで、なぜ埃は部屋の隅にたまるのでしょうか? その訳は、部屋の中ほどは窓からの風が通ったり人が歩いたりして比較的強い風が吹いて埃が動きやすいのに対して、部屋の隅では風が弱くて埃があまり動かないからではないでしょうか。以上のことをモデル化して、この現象を Python で再現してみましょう。
なお、ここでは乱数(random module)とグラフ(matplotlib.pyplot)を使いますので、プログラムの最初にそれぞれのモジュールを読み込み(import)ます。
import random
import matplotlib.pyplot as plt埃が風に舞う
ここでは話をシンプルにするために、まず埃1つだけで考えましょう。また、平面ではなく、数直線の -1 と +1 の間を埃が動くと考えます。0 の位置が部屋の真ん中で、-1 と +1 の位置が部屋の隅という想定です。
これくらい条件をシンプルにすれば、なんとかなるでしょうか。さて、次の問題は「この埃をどうやって動かすか」です。
まず「+0.5 から -0.5 までの一様な乱数」…(1) を、不規則な風に見立てましょう。このとき、左向きの風はマイナスで、右向きの風はプラスで表されています。
次に、その値を部屋の中ほどでは強く、部屋の隅では弱くなるように調整しましょう。そのために「部屋の隅から埃までの距離」…(2) を表す式を作ります。
そして①と②を掛けた値を「埃の移動距離」…(3) とすれば、「部屋の中ほどでは比較的強く、部屋の隅では比較的弱い不規則な風に乗って移動する埃」がモデル化できます。
さらに直前の「埃の位置」に③を足した値を新たな「埃の位置」…(4) とします。その上で「埃の位置」をグラフ化すれば、1つの埃が風に舞って移動する様子がシミュレーションできます。
《コード1》
1 import random
2 import matplotlib.pyplot as plt
3 position = 0
4 for i in range(50):
5 wind = random.random()-0.5 # (1) 不規則な風
6 distance = 1-abs(position) # (2) 壁からの距離
7 move = wind*distance. # (3) 埃の移動距離
8 position = position+move. # (4) 新たな埃の位置
9 plt.scatter(i,position)
10 plt.show() 実際に関数式を組もうとすると、一番苦労するのは (2) の「部屋の隅から埃までの距離」でしょうか。壁が2か所あるので、そのうちの「近い方」までの距離を表す式を立てたいわけですが、さてどうしましょうか。
期待通りの動きをするまであれこれ試行錯誤していただきたいところですが、方法は3つくらいあります。
○ distance = 1-abs(position)
○ distance = min(1-position,1+position)
○ if position > 0:
distance = 1-position
else:
distance = 1+position 2番目の式がわかりやすいでしょうか。翻訳すると、つまり「(1-position)と(1+position)のうち小さい(min)方」ということです。同じことを1番目の式では絶対値(absolute)関数 abs を使って、3番目の式では if 関数を使って実現しています。
またプログラムの9行目「plt.scatter(i,position)」は for 文の中にあって、移動する点の位置を都度記憶しています。10行目「plt.show()」は for 文の外にあって、ここで点の位置を一気に表示(show)して、点が動く様子を表しています。
2回「実行」したところ、次のようなグラフが描けました。横軸が「時間」、縦軸が「埃の位置」です。
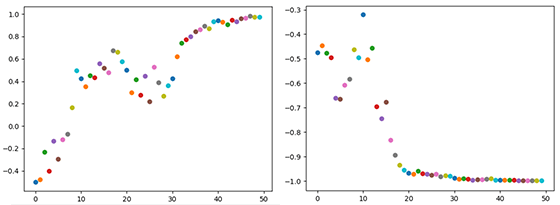
埃がふわふわと部屋の隅に移動していく様子が見て取れますね。
ところで、埃の動きを「散布図」つまり点だけで表示するより、「折れ線」でつないで描く方がわかりやすいかもしれません。ところが、それをやろとすると、一手間増えるんです。なぜかと言うと「散布図の点どうしは無関係でそれぞれ単独で表示できる」のに対して、「折れ線グラフでは隣どうしの点の位置が影響する」からです。
というわけで、今は折れ線グラフには行かずに、散布図のままで次に進みます。次のプログラムでは、散布図のままの方がむしろ良いのです。折れ線グラフについては、この記事の最後に付記します。
埃は部屋の隅にたまる
「1つの埃」でうまく出来たら、次は「たくさんの埃で」やってみましょう。「埃1つ」の場合に for 文のループを作りましたので、「たくさんの埃で」やるためには for 文の2重ループを作れば良さそうですね。
《コード1》と比べると、3行目に大回りの for 文(変数j)を挿入しました。その結果、全体の行数が1行だけ長くなりました。他にはほとんどいじっていないのですが、1カ所だけ、ほんのちょっとだけ変わっていることに気がつくでしょうか。
《コード2》
1 import random
2 import matplotlib.pyplot as plt
3 for j in range(100):
4 position = 0
5 for i in range(50):
6 distance = 1-abs(position)
7 wind = random.random()-0.5
8 move = wind*distance
9 position = position+move
10 plt.scatter(j,position)
11 plt.show() 《コード1》の9行目、《コード2》では10行目が、ほんのちょっとだけ違っています。見た目はどちらも同じように見えます。でも、先ほどは内側の for 文の中にあったものが、ここでは内側の for 文の外、外側の for 文の中にあるのです。また、それに連動して、変数がiからjに変わっています。
これだけの違いなのですが、これゆえに表示(プロット plot)する点の意味が違ってきます。《コード1》では「1つの埃が動いていく、その時系列の位置」を表すのに対して、《コード2》では「たくさんの埃が動いて、最後にたどり着いた位置」を表すわけです。
100 個の埃の位置を 50 単位時間まで動かしたのが、次のグラフです。部屋の隅の方に埃が多く集まり、中ほどには少ない様子が見て取れますね。
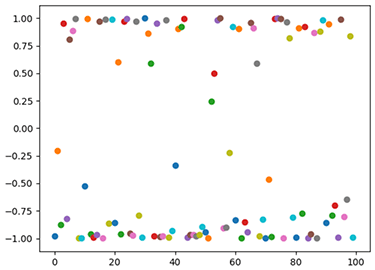
ところで、散布図は高校数学1の「データ分析」の項目で相関係数とともに出てくるグラフですから、高校生にとっては馴染みのあるグラフです。その散布図がここではビジュアルに効果的に使えていますね。
「埃1つ」の方も「たくさんの埃」の方も「実行ボタン」を押せば何度でもシミュレーションできます。ふわふわ、ふらふら、こんもり、ぱらぱら、楽しいですよ。
折れ線グラフの作り方
《コード1》と《コード2》では「散布図」を描きましたが、ここでは「折れ線グラフ」を描いてみましょう。
でも、そのためには一手間増えます。リストを使います。しかも x 座標の分(3行目と9行目の t 、時間に当たる)と y 座標の分(4行目と10行目の position 、埃の位置)と2つのリストを使います。 for 文で50回転する間に、t は1つずつ増え、position は風に押されてふらふら動きながら、リストに値が追加されていきます。
1 import random
2 import matplotlib.pyplot as plt
3 t=[0]
4 position = [0]
5 for i in range(50):
6 distance=1-abs(position[i])
7 wind = random.random()-0.5
8 move = wind*distance
9 t.append(i+1)
10 position.append(position[i]+move)
11 plt.plot(t,position)
12 plt.show() そして for 文での50回転が終わったところで、for 文の外、11行目で一気に折れ線グラフを作って、12行目でそれを表示しています。
2回シミュレーションしたところ、次のようなグラフが描けました。
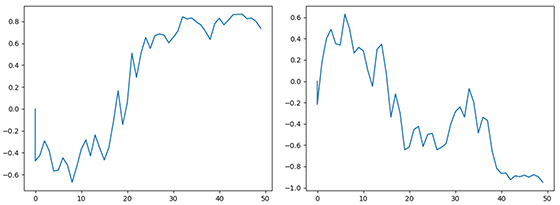
確かに「1つの埃」の場合は「折れ線グラフ」の方が、でも「たくさんの埃」の方は「散布図」の方が見やすいですね。
◇ ◇ ◇
〜 Python でシミュレーションする 〜
▷ Python で情報伝達を見える化する
▷ Python でサイコロを振ってみる
▷ Python で埃をシミュレーションする
