コロナ渦中の確率計算

PCR検査実施数はどれくらいが適当か？

　ある病気に感染している人の割合（感染率）を 1％ とします。また、その病気に感染しているか否かを調べる検査の精度を 99％ とします。すなわち、感染していないのに陽性反応が出る確率が 1％ で、感染しているのに陰性となる確率も 1％ です。
　ある人がその検査を受けたところ、陽性反応が出ました。さて、この人が実際に病気に感染している確率はどれくらいでしょうか。

 「検査の精度が 99％ なら、実際に感染している確率はかなり高いだろう」と思うのではないでしょうか。でも、実は意外と低いのです。この問題、高校・数学でいうと「条件付き確率」の問題ですが、なかなか分かりにくい問題だと思います。
　計算してみましょう。便宜上、検査を受ける人数を 10,000人 とします。このうち感染しているのは 1％ の 100人 … ① で、感染していないのは 9,900人 … ② です。検査で誤った判定が出る確率は 1％ ですから、① のうち 1％（＝1人）には陰性反応が出て、② のうち 1％（＝99人）には陽性反応が出ます。
　以上から、受検者 10,000人 を「感染しているか、否か」と「陽性か、陰性か」で４つに分類すると、次表のようになります。

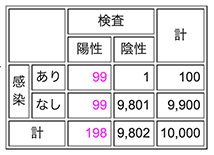
　表から、この検査で陽性反応が出るのは全部で 198人 で、そのうち実際に感染しているのは 99人、実は感染していない人も 99人 だということが分かります。ということは、「陽性反応が出た人が実際に感染している確率」は 50％ です。意外と小さいと思いませんか。

　そのことを面積図で説明しましょう。次図中の「有・無」は感染の有り・無しです。「正・誤」は検査結果が「正しいか誤りか」です。色付きの部分が「陽性」が出る部分で、確率を計算するときの分母になります。このうち「実際に感染」しているのは図左上の横長の部分で、確率を計算するときの分子になります。上の例では２カ所の面積が同じなので、確率は 1/2 になるというわけです。

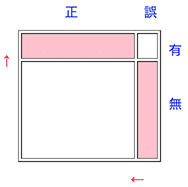
　では、ここで現実の新型コロナ・ウィルス感染症とPCR検査に引き寄せて考えてみましょう。（2020年5月執筆）
　上では計算しやすいように「感染率 1％、検査の精度 99％」と仮定して計算しましたが、新型コロナ・ウィルスの感染率は 1％ よりはもっとずっと低いでしょうし、PCR検査の精度も 99％ よりもっと低いでしょう。感染率が低いと、図の横長の部分がもっと薄くなります。検査の精度がもう少し低いと、図の縦長の部分がもっと厚くなります。つまり、先ほどの確率計算において、分母が大きく、分子が小さくなるわけです。
　例えば、感染率が 0.1％、検査の精度が 90％ なら、分母がざっくり 10倍 に、分子がざっくり 10分の１ になるわけですから、先ほどの確率 50％ がいきなり 100分の１ ほど、つまり 0.5％ 程度になってしまうわけです。
　というわけで、この手の検査を闇雲にやると「陽性が出た人のうちで実際に感染しているのは１％未満」みたいなことになりかねないわけです。

携帯電話位置情報の正しい使い方

　新型コロナウィルス感染拡大に伴う緊急事態宣言発令中の頃の話です。政府から「接触８割減を目指す」というようなことが言われました。時を同じくして、携帯電話各社から携帯電話の位置情報を基にして「外出数が以前と比べてどれくらい減っているか」の情報が出されました。そして「８割減にはまだ達していない」とか「８割減には程遠い」とか報道機関がそんな言い方をしているのをよく目にし、耳にしました。（2020年5月執筆）
　でも考えてみると、「接触率」と「外出率」は別物ですよね。さて、「接触率≒外出率」なのでしょうか？　そもそも接触率と外出率は比例するのでしょうか？
　ここで「外出する人の数が８割減」になったときに「接触率がどうなるか」を考えてみましょう。自分が外出する機会が２割に減って、外出した先でも人出が２割になっていれば、自分が接触する人数はこれまでの 0.2×0.2＝0.04倍に、すなわち96％減になりますよ。つまり「接触率は、外出率の２乗に比例する」のです。もちろん現実には「濃厚か否か、接触している時間」などによって違うのでしょうけれど、おおよそそのようにみなして良いだろうと思います。少なくとも「外出率≒接触率」という想定よりはよほど実態に合うはずです。
　「外出する人の数が８割減れば、接触率は単純計算して96％減る」のです。でも、そこまでやらなくても良いんじゃないですか？　接触が少ないに越したことはないのでしょうけれど、目標が「接触８割削減」なら、これは「やりすぎ、過剰対応」ということになるのではないでしょうか。

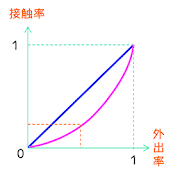
 では、外出率がどれくらい減れば「接触８割減」が達成されるかというと、ざっくり言えば「外出する人の数が半分に」なれば良いんです。各自が外出する機会が半分になって、外出した先でも人出が半分になっていれば、各自が接触する人数はこれまでの４分の１に、すなわち75％減になります。８割減にはちょっと届きませんが、これでほぼほぼクリアです。
　携帯電話の位置情報は外出率を見るのにとても良いデータです。けれども、それは接触率とは違う。ビッグデータも意味を考えずに数字だけを見るのは、誤解の元です。ビッグデータを扱う上で大事なのは、やはり世の中を見る目線でしょうね。
　新型コロナ禍の中で指数関数・対数関数はしばしば目にしました。指数関数的な増え方、対数処理を施した統計資料などです。そんな中で「接触率は、外出率の２乗に比例する」件は２次関数に出会えた稀な例でした。
　なお、この件は「接触率＝外出率」と想定するモデルと「接触率は外出率の２乗に比例する」と想定するモデルの立て方の違いとも言えます。そしてモデルの立て方が違えば、当然のことながらシミュレーション結果も変わります。携帯電話位置情報から得られた外出率が例えば以前の「６割減」であったとして、その情報から「接触８割減の目標」に達していると見るのか、達していないと見るのか、それくらいの結構大きな差になるわけです。

前年同月比の振る舞い

　先日のニュースで言っていました。（2020年4月執筆）

2020年３月の訪日外国人旅行者数が前年同月比で93％減になった。

もちろん新型コロナウィルスの影響です。では、ここで【問題】です。

もし１年後に訪日外国人旅行者数が元に戻ったとすると、2021年３月の訪日外国人旅行者数は前年同月比で何％増になるでしょうか？

　続いて、もう１問。（データを調べなくても、常識で考えればわかります）

2011年３月にも訪日外国人旅行者数が前年同月比で大幅に減少しました。東日本大震災の影響です。次の空欄に当てはまる数を入れてください。
○　前年同月比マイナスは2011年３月から〔　〕ヶ月間続き、
　　その翌月に前年同月比が急上昇した。

　ところで、なぜ「前年同月比」が使われるかと言うと、季節変動がある（季節によって旅行者数が変わる）からですが、前年同月比を異なる月で比べたり、月ごとの推移を見たりすると、一見奇妙なことが起きます。

　訪日外国人旅行者数の実際の数を見る前に、架空の数で説明しましょう。
　ある企業の月ごとの売上額が次表の通りだったとします。何かの事情で2011年3月に売上額が急減しました。そのときの売上額から前年同月比を求めて、グラフにしてみました。

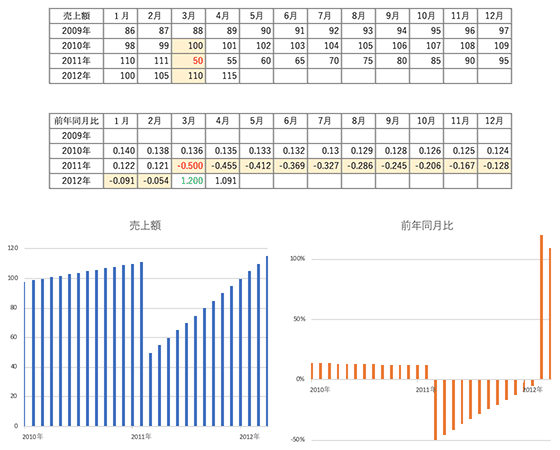
　売上額のグラフを見てわかるように、2011年３月に１回だけ売上が大幅に減って、それ以降は順調に売上が回復しています。これを前年同月比で見ると、12ヶ月連続のマイナスとなり、13ヶ月目に120％の大幅プラスとなりました。前年同月比だと、えてしてこうなってしまうわけです。

　次に、実際の訪日外国人旅行者数を見てみましょう。下のデータは 日本政府観光局 のサイト（→ https://www.jnto.go.jp/jpn/statistics/visitor_trends/ ）で公表しているものです。

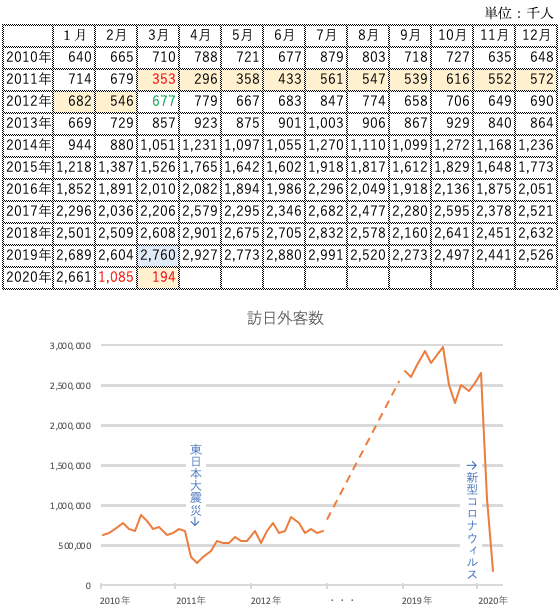
　東日本大震災のころを見ると、前年同月比は2011年３月から12ヶ月連続でマイナスとなり、その翌月の2012年３月には前年同月比で 677÷353＝1.92 すなわち 92％ の大幅プラスになっています。考えてみれば、当たり前のことですが。
　次に直近の2020年３月を見てみると、前年同月比で 194÷2760＝0.07倍に、すなわち 93％ の大幅ダウンになっています。この先どうなるかはわかりませんが、おそらく東日本大震災のときと同じように「前年同月比は12ヶ月連続でマイナスとなり、その翌月に一転して前年同月比で劇的にプラス」となることでしょう。
　さて2021年３月にどれくらい劇的にプラスになるのか、仮にその時点での訪日外国人旅行者数が元の水準 2,760千人 に戻るとして、試しに計算してみましょう。この場合、93％減から元に戻るからと言って、93％増になるわけではありませんよ。きちんと計算してみると、前年同月比で 2760÷194＝14.2 倍に、すなわち 1320％プラスということになります（「７％」という値から計算すると、100÷7＝14.3 より 1330％プラスとなります）。実際には毎月少しずつ回復するのでしょうけれど、前年同月比で見ると、そんな風に見えるわけです。「前年同月比のマジック」ですね。

◇　　　　　　◇　　　　　　◇

〜 新型コロナで確率・統計を学ぶ 〜
▷ コロナ渦中の確率計算　　　　　　
▷ サッカー観戦でコロナ感染者集計　
▷ 情報伝達をグラフに＝見える化する