
ひもを結ぶ問題
前の記事「場合の数の数え方 と 確率の数え方 の違い」の続きです。
【2】ひもが3本ある。両端6個を2つずつに分けて3回結ぶとき、
大きな1つの輪ができる確率を求めよ。
【1】の解説をしながら私が熱く訴えたのは、
確率を計算する際に「何を区別して、何をしないのか」は問題文にどう書いてあるかは関係ない。
「同様に確からしい」を守ることが絶対条件で、何でもかんでも区別すればそれは守られるが、けれどもそれでは場合の数が増えてしまって数え上げるのが大変になるので、「同様に確からしい」が守られる範囲で「区別しないで済むなら、区別しないで数えた方が楽」。
そういう話でした。この問題でいうと、
ひもを区別するのかしないのか? 両端を区別するのかしないのか? 結ぶ順番は?
それらをどうするか、ということです。ところで、この問いに対して、次のように質問する人が必ずいます。
この問題ではひもには区別があるんですか? それとも区別がないんですか?
と。でも、考えてほしいのですが、
赤・青・黄の3本のひもを結ぶ場合と、全く同じような3本のひもを結ぶ場合とで、「大きな1つの輪ができる確率」が変わるだろうか?
変わりませんね。同じです。ひもに限らず、ひもの両端でも、結ぶ順番でも同じ話になりますが、
「区別があるのか、ないのか」という設問の条件(出題者側の問題)ではなくて、「区別して数える方が簡単か、区別しないで数える方が簡単か」という解答者側の数え方(判断)の問題だ
ということです。ここでちょっと話を端折りますが、結論的に言うと、この問題では
ひもと両端を区別するのは必須。そうでなければ「同様に確からしい」が守られない。
一方で、結ぶ順番とどちらの手で取るかは区別してもしなくてもどちらでも良い。
ことになります。では、そろそろ計算を始めましょう。まずは総数から。
まず「6個の両端から2つを選んで」結びますね。その場合の数は $${_6\textup{C}_2}$$ 。ちょっとここで確認しましょう。$${_6\textup{C}_2}$$ の 6 は「異なる 6 個の中から」という意味でしたね。つまり $${_6\textup{C}_2}$$ と書いた時点であなたは「両端 6 個を区別した」のです。
続けましょう。「残り4個から2つを選んで」結ぶのが $${_4\textup{C}_2}$$ 通り、残った2個を結ぶのは1通り。
よって、総数は $${_6\textup{C}_2\times\,_4\textup{C}_2}$$ 通り。
ところで、次のような場合、あなたは何通りと数えますか?
6人の人を2人ずつの3つのグループに分ける
やったことのある問題だと思いますが、この場合は $${_6\textup{C}_2\times\,_4\textup{C}_2\,\div3\,\textit{!}}$$ とやるのではないですか?
さて、ひもの問題で $${3\,\textit{!}}$$ で割りますか? それとも割らずにいきますか? というより、ひもの問題で $${\textbf{3\,\textit{!}}}$$で割る場合と割らない場合とでは、何を区別したことになるのでしょう? もしくは何を区別しなかったことになるのでしょう?
この問題で悩むのは、そこかもしれません。結論的に言うと、3!で割っても割らなくてもどちらでも良いのです。総数を $${_6\textup{C}_2\times\,_4\textup{C}_2=90}$$通り でやっても、$${_6\textup{C}_2\times\,_4\textup{C}_2\,\div3\,\textit{!}=15}$$通り でやっても、どちらでも出来ます。
ただ、どちらで数えるかによって「大きな1つの輪ができる場合の数」も変わります。そしてもちろん、総数(分母)の数え方と「大きな1つの輪ができる場合の数」(分子)の数え方は同じでなければなりません。すなわち、分母で区別したものは分子でも区別し、分母で区別しなかったものは分子でも区別せずに数えなければならないのです。
だから、ここでしっかり考えましょう。「 3!で割るのか、割らないのか?」、「 3!で割るのと割らないのとでは、何が違うのか?」、「 3!で割って総数90通りでやるのと、 3!で割って総数15通りでやるのとでは、どっちが楽か?」。そう考えると、この点は大問題だと思いませんか。
話を少し戻しましょう。3!で割る場合と割らない場合とでは、何を区別したことになるのでしょう? もしくは何を区別しなかったことになるのでしょう?
答えは「結ぶ順番」です。3!で割ると結ぶ順番を区別しないで数えたことになり、3!で割らないと結ぶ順番を区別したことになります。わかるでしょうか。
さて、どっちが楽か。たぶん結ぶ順番を区別しない方が楽でしょう。その方が総数が少ないですし、分子を数えるときも結ぶ順番を区別しない方が楽ですから。
というわけで、総数を 6C2×4C2÷3!=15通り として計算することにしましょう。そうすると、次に分子の場合の数を求めればいいですね。
いや、ごめんなさい。もう少し確認させてください。とりあえず前に戻ります。というのは、設問の状況を考えると、実際には結ぶ順番があるのです。同時に3つを結ぶことなんて出来ませんから。
にもかかわらず、結ぶ順番を区別しないことにしたのです。それは私たちの判断です。前にも言いましたね。
確率を計算する際に「何を区別して、何をしないのか」は問題文にどう書いてあるかは関係ない。
と。ついでにもう一つ確認しましょう。総数を数えるときに、順列の P ではなく、組合せの C で計算しましたね。順列 P で数えるのと組合せ C で数えるのとでは、何が違うのでしょう。何を区別しているのか、もしくは何を区別していないのか、言えますか。
6P2 と 6C2 の違いは「異なる6個の中から2個取り出すとき、取り出す順番を区別するか、しないか」です。取り出す順番を区別して数えるのが順列 P で、取り出す順番を区別しないで数えるのが組み合わせ C です。それはそうと、このひもの問題で P で計算するのと C で計算するのとでは、具体的に何を区別したり区別しなかったしていることになるのでしょう。
それは言うなれば「ひもを結ぶときに右手で取るのと左手で取るのとを区別するのかしないのか」ということです。ひもの端aを右手で取りbを左手で取る場合と、逆にaを左手で取りbを右手で取る場合を区別するなら順列 P、区別しないなら組合せ C で計算することになります。上では組合せの C で計算したわけですからそれを区別しなかったというわけですが、これも実際には片手で2本のひもを結ぶことはできませんから、問題文の状況に忠実に計算するなら、順列の P で計算してもよさそうなものです。でも何度も言うように、
「同様に確からしい」が崩れないなら、区別しないで数えた方が楽
だからそうしたわけです。奇妙に感じるでしょうか。この問題では
ひもと両端には区別がないのに、区別して数え、結ぶ順番とどちらの手で取るかは区別があるはずなのに、区別せずに数えよう
というわけです。そして、そのように数えるのが確率のコツなのです。
次に考えるべきは、分子(大きな1つの輪ができる場合の数)です。さて、これは何通りでしょうか。1通りではありませんよ。分母を数える際に「ひもと両端を区別して、結ぶ順番とどちらの手で取るかは区別しなかった」のですから、分子を数える際にも同じように数えなければなりません。
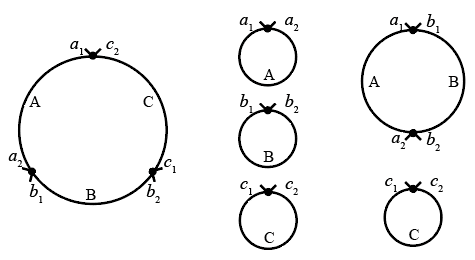
上左図はその1例です。ひもと両端を区別すれば、他にもあります。その場合の数は
ひもBとひもCの入れ替え、
ひもBの端 b1 と b2 の入れ替え、
ひもCの端 c1 と c2 の入れ替え、
これらを計算すると、2×2×2=8通り となります。
念のため他の2つのパターン、すなわち「小さな円が3つできる場合」(上中図)、「中くらいの円が1つと小さな円が1つできる場合」(上右図)についても数えてみましょう。3のパターンを合わせて 15通り になるはずですから。
「小さな円が3つできる」のは、結ぶ順番を区別しないのだから、1 通り
だけです。上中図以外にはありえません。また
「中くらいの円が1つと小さな円が1つできる」のは、
ひもA,B,Cの入れ替えが 3 通り
ひもBの端 b1 と b2 の入れ替えが 2 通り
ですから、3×2=6通り です。
以上3パターン合わせると、8+1+6=15通り。総数と合いましたね。これで確信がもてたでしょう。
というわけで、【2】の答えは 8/15 です。
ところで、実は別解もあります。おそらく別解の方がわかりやすいでしょう。
まず1本のひもの片方を手に取ってください。さて、それを何と結びましょうか?
候補は5つありますが、同じひもの反対側の端と結んだら大きな輪にならないので、結んで良いのは5つのうちの4つ。つまり確率 4/5 … ①。
次に、いま結んだひもの反対側の端を結びましょう。候補は3つありますが、大きな1つの輪にするために結んで良いのは3つのうちの2つ。つまり確率 2/3 … ②。
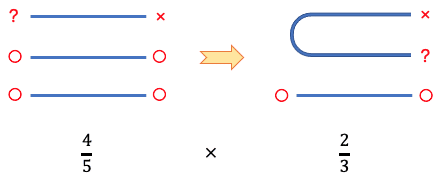
求める確率は ①×②= 8/15 。
この問題の答えを得るだけならこちらの別解の方が良いようにも思いますが、ここでは「何を区別するのか、しないのか」の練習という意味合いを込めて、初めのやり方で解いてきました。悪しからず。。。
◇ ◇ ◇
〜 確率名人への道 〜
【1】 場合の数の数え方 と 確率の数え方 の違い
【2】 ひもを結ぶ問題
【3】 だまされやすい確率
【4】 気づきにくいダブりとモレ
【5】 数学でアクティブ・ラーニング例
