New Method for Solving the Collatz Conjecture 2 with High-Prize Money
Chapter 2: Derivation of CS -Vibration and CS-Plot (article 2)
Please read "Introduction to a New Method in Chapter 1 (article 1)" before reading Chapter 2 (article 2).
Although CS-vibration is introduced in "Before Explaining the New Method in Chapter 1, Section 1.9", it is reprinted (with some changes and additions) in Section 2.1.
Chapter 1 also posts links to each chapter.
When translating from Japanese to English, subtle nuances of the original articles may not be fully conveyed. If you would like to view the original Japanese articles, please see Chapter 1 of Japanese Article 1.
Summary Video of the New Method in English
2.1 What is CS-Vibration
Regarding the Collatz conjecture rule:
For odd numbers, triple the number and add 1.
For even numbers, divide the number by 2.
Since any even number will eventually reach an odd number through repeated division by 2,
Only odd numbers will be tracked, while even numbers will be omitted unless specifically mentioned.
For example, in the case of 13 from Section 1.1, Only the odd numbers will be shown: $${13 \to 5 \to 1}$$
The total number of steps until reaching 1 is the total number of $${\to}$$, which in the case of 13 is 2.
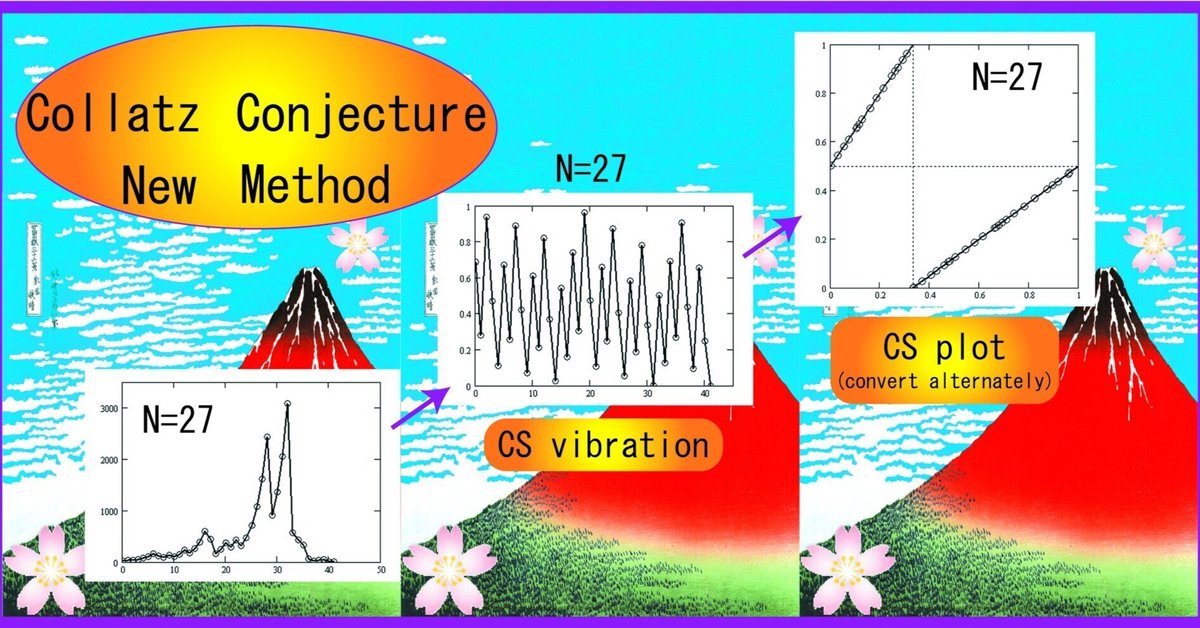
Let $${No}$$ be an odd integer. Although $${No=27}$$ is a small number, it has a total of 41 steps as shown below.
Only odd numbers are tracked and the maximum number is 3077.

Figure 1-2 shows the odd number changes on the horizontal axis (step number 0 for 27, step number 41 for 1) and the odd number values for each number on the vertical axis.
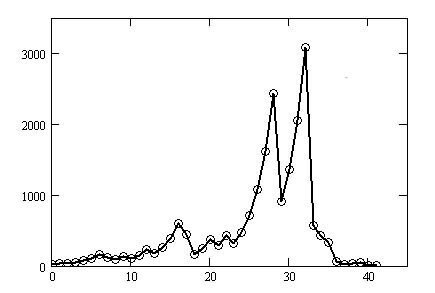
When the graph in Figure 2-2 is transformed using the new method,
the result is Figure 2-3.
This is referred to as the CS-vibration, where C also refers to the C of the Collatz conjecture.
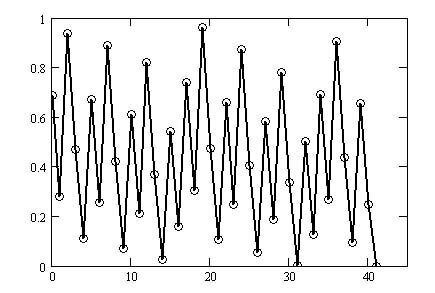
Figure 2-3 shows more regularity and periodicity than Figure 2-2.
This regularity is just the beginning, and I will apply several more transformations. This will reveal even clearer regularity.
The same tendency appears for initial values other than 27, albeit with a difference in the number of steps.
Finally, in Chapter 6, I will present a general formula and proposition that explain this tendency for any odd integer $${No}$$.
I will explain Section 2.2 of Chapter 2 in order.
Section 2.2 is a paid article in Chapter 2, but I would like you to make a decision after looking at the CS-vibration diagram (Figure 2-3). In addition, Section 4.1 of Chapter 4 (summary of previous chapters) and Figure 4-1, as well as the contents of the following chapters, are also very helpful.
Figure 2-3 shows the CS-vibration graph for $${No=27}$$. Section 2.2 presents a formula for deriving CS-vibration graphs for general odd numbers $${No}$$.
Furthermore, this formula allows the classification of the coordinate points appearing in the CS-vibration into two types. The characteristics of these types are explained using the example of $${No=27}$$.
The general proof of the linear equation representing the two types is a key proof, and it has been made a separate section 2.3 and a separate article in the same chapter.
These two types of linear equations are also very important. The above coordinate points can be expressed "approximately" by the two types of linear equations as they are. However, by applying a certain transformation, all the intermediate steps of odd numbers for the initial value of any odd number $${No}$$ can be "completely" put on the points on this line.
This means that all the odd numbers $${\bm{No}}$$ of all steps are on the two types of linear equations (see Chapter 4, Figure 4-1).
I will devote a chapter after Chapter 3 to this explanation, including the background.
If you want to get a hint to solve the Collatz conjecture and want to know more about it, please read the following chapters.
I have made every effort to make the proof as easy to understand as possible using high school mathematics. If you find the content of the article to be "I see", please rate it. It will encourage me to continue my analysis in the future.
Variables, Definitions, and Functions up to Section 2.2 in Chapter 2:
$${N}$$, $${No}$$,
total number of steps, step number, CS-vibration, C-transformation,
CS-plot, CS-linear-equations
$${c(N_o)}$$, $${z_{s}}$$, $${f_{c}(x)}$$, $${f_{s}(x)}$$
The new method is introduced in Articles 1-10 and Chapters 1-8.
The translation from Japanese to English has been completed for all articles, both free and paid. (April 2024)
2.2 Derivation Formula of CS-Vibration and CS-Plot
ここから先は
¥ 800
Amazonギフトカード5,000円分が当たる
この記事が気に入ったらチップで応援してみませんか?
