
コラッツ予想解明への新解析手法の紹介1ー 問題の意味が小学生でもわかる数学の高額懸賞金歴史的未解決問題

リンク
「(続)コラッツ予想解明への新解析手法の紹介」では第C1章からご覧ください。
第C1章には(続)新解析手法の各C・章へのリンクが貼ってあります。
↓「コラッツ予想解明への新解析手法の紹介」のリンク
第2章 CS振動の導出とCSプロット
2.1 CS振動とは
2.2 CS振動の導出式とCSプロット
第2章 CS振動の導出とCSプロット
2.3 CS直線式の導出とCSプロット点との関係
第3章 奇数の分類
3.1 奇数の分類(Nc型とNs型)
3.2 Nc型とNs型の特性
第4章 奇数の分類とS変換の関係
4.1 前章までの概要
4.2 S変換の定義と具体例
4.3 S変換の導出
4.4 S変換の特性
第5章 カオス力学1次元写像
5.1 コラッツ予想(CS空間)と1次元写像の類似性
5.2 テント写像(1次元写像の例)
【休憩室】モンスターハンター
第6章 コラッツ予想と同値なCS空間上の命題
6.1 コラッツ予想と同値なCS空間上の命題(弱い命題)
第6章 コラッツ予想と同値なCS空間上の命題
6.2 コラッツ予想と同値なCS空間上の命題(強い命題)
6.2.1 弱い命題は親の脛齧り but 成長が遥かに上回る
6.2.2 強い命題は親から独立 and 更に大きく成長
6.2.3 CS交互変換プロット
6.2.4 コラッツ予想と同値なCS空間上の命題(強い命題)
6.2.5 6 . 2 全般の定量的追加説明
第7章 コラッツ予想は攻略できる?できそう?できるかも?
7.1 正攻法では牙城を崩すのは難しい
7.2 ベルヌーイシフト(二進変換)写像
7.3 解明へと新分野
第8章 出会い
8.1 出会い
8.2 チャレンジできそうな他未解決懸賞金問題
【休憩室】中学高校受験生のための合格必勝いろは歌
A1 現代いろは歌について
A2 中学高校受験生のための合格必勝いろは歌
A3 合格必勝いろは歌各種画像
第1章 新手法の紹介の前に
1.1 コラッツ予想とは
問題の意味は小学生でもわかるのに80年以上未解決の数学の歴史的問題にコラッツ予想があります。1億2000万円の懸賞金も日本メーカからかけられています。笑わない数学番組でも紹介されました。
コラッツ予想を初めて知った方もこのサイトを訪れている場合もありますので、また中高数学でわかるように新手法(新しい見方)を解説したいと考えています。
コラッツ予想とは「全ての正の整数において、奇数なら3倍して1を足す、偶数なら2で割る、を繰り返していくと、どんな正の整数でも有限回数で1に到達する」というきわめてわかりやすい予想です。
一例として13を例にとります。13は奇数なので3倍して1を足すと 40になります。40は偶数で2で次々と3回割れて5になります。5は奇数なので3倍して1を足し16になります。16は偶数で2で次々と4回割れて1になります。$${13 \to 40 \to 20 \to 10 \to 5 \to 16 \to 8 \to 4 \to 2 \to 1}$$。
また1は $${1 \to 4 \to 2 \to 1}$$と唯一ループします。
現在までに$${2^{68}}$$までの数字が1に到達することが確かめられています。このことは、$${2^{68}}$$以下の数字では、1以外はどの数字も同じ数字に戻ることはなく(ループしない)、また限りなく大きくなっていくこともない、ということです。
1.2 コラッツ予想は解けた?
世界で最も有名な数学者の一人であるフィールズ賞をもつ天才テレンス・タオが2019年9月、査読前論文プレプリントをarXiv(アーカイブ)に殆ど全ての正の整数について殆ど正しいことを公表しました(論文は2022年5月に出版)。彼でさえ、完全証明はまだまだと述べています。
予想が正しいことをいうためには以下の2点を証明する必要があります。
・すべての正の整数でどこまでも大きくはならない
(最大値が存在する、無限ステップ数とはならない)
・1を除くすべての正の整数でもとに戻ることはない
(ループしない)
この2点が証明できれば有限回数でいつかは1に到達することになります。
1に収束する、つまり無限回で1に到達することが言えてもダメですし、
特定の正の整数だけで表やグラフにして1に到達することが言えた、つまり1に到達する傾向が見えたでもダメです。その傾向が見えたならすべての正の整数で成立するように一般化する必要があります。ネットでよく見かけます。
逆に反例であれば、1に到達しないある正の整数1つ発見できればOKです。
1.3 有名なアマチュア数学家
歴史上の数学の難問を解いたり、数学の歴史に残る業績を残した人物はプロの数学の学者さんばかりではありません。
フェルマーの最終定理で有名なピエール・ド・フェルマーはフランスの裁判官であり、数学は趣味として行っていました。彼は「数論の父」とも呼ばれ、数学における多くの重要な貢献を行いました。
四色問題を解いた一人であるアルフレッド・プレイ・ケンプはロンドンの法廷弁護士であり、アマチュア数学者でもありました。(後に不備が指摘されましたが、ケンプの証明で使われた論理に沿って、地図を塗り分けるには5色で十分であることが証明されました(五色定理)。)
フランスの数学者、エヴァリスト・ガロアは群論とガロア理論への基礎的な貢献を行っていて、これらは現代数学において不可欠なものです。
こうした業績は、多くのアマチュア数学者が分野に重要な貢献をしてきた、ほんの一例です。彼らの仕事は、数学的才能と創造性はあらゆる階層の人々の中に見出されており、情熱と献身が画期的な発見につながりうることを示しています。
数学の難問を解くことは専門的な訓練を受けた数学者だけでなく、一般の人々にも開かれていることが伺えます。
また大学院生であったジョージ・ダンツィーグは黒板に書かれていた統計学の未解決問題を宿題と勘違いして解いてしまったのだそうで、映画の題材にされたそうです。いつどこでだれが未解決問題を解いてしまうか、神のみぞ知るです。
1.4 ノーベル賞よりも後世に名が残る?
ノーベル賞授賞式は毎年行われ、物理、化学、医学等の各分野で最高3人まで同一テーマで受賞できます。歴史にも当然残ります。100年経てば各分野で300人が、200年経てば600人が歴史に名を刻みます。しかしながら300人、600人ともなりますと偉人であっても名としましては薄れていくように思います。
一方で数学の歴史的未解決懸賞問題を解決できた人物はフェルマーの最終定理を解いたアンドリュー・ワイルズやポアンカレ予想を解いたグリゴリー・ペレルマンだけです。他未解決問題を40歳以下で解明すれば数学のノーベル賞と言われるフィールズ賞も貰えるかもしれません。
個人的には後者の方がより後世に名を残していると思っています。
1.5 数学は発明か発見か
結び目理論は一致しない結び目の種類に関する理論ですが、一見しますと、これがわかれば何の役に立つと思われそうです。しかしこの理論が宇宙の法則と関係していたことが見出されました。数学は「発明」か、それとも人類とは無関係に宇宙に存在していた、人類が知らないだけであり、「発見」しただけなのか(結び目理論番組)。
コラッツ予想もその真理を人類が知らないだけであることは否定できません。コラッツ予想に限らずです。非常に感慨深いです。
1.6 解いている過程でも
数学以外の科学の分野では実証に実験が必要になる場合も多く諸費用がかかります。一方数学の場合は実証には解析用パソコン1台あればほぼ間に合います。家に居ながらにして解析ができます。世間や人の目を気にすることもありません。
解いた時には栄光が待っています
数学の歴史的未解決問題(100万ドル懸賞金問題)はいくつかありますが、コラッツ予想が最も入りやすい問題だと思います。パズルや入試問題等を解くことが好きであれば、ぜひチャレンジしてみてはいかがでしょうか。
人生は誰でも一度きりです
解いている過程でもいろいろな副産物が生まれることがあります
ユーリ・マチャセビッチはヒルベルトの第10問題の解決の副産物として
19変数の多項式からなる素数を作る式を生み出しました。
女性数学者であったフランスのソフィ・ジェルマンは、フェルマー予想を奇素数に対して正しいことを証明しました。当時は女性が数学者になることは許されず、ルブランという男性名でガウスやルジャンドルと文通して研究していて、それを高く評価したガウスがゲッチンゲン大学の名誉学位を与えたそうです。先駆けとなる証明で歴史に名を残しています。
素数に関しては、整数論ひいては数学の金字塔、「素数はどのような規則で並んでいるのか」、という小学生でも問題の意味がわかる法則は未だに見出されていません。数多くの偉人が解明の過程で多数の定理や理論を残してくれました。素数百科もあるくらいです。
1.7 別分野で解く,チャレンジする
ある分野の問題を別分野で解くことにより、その分野がより発展することもあります。
素数が無限個存在する証明は紀元前の古代ギリシャ時代にユークリッドが証明していますが、オイラーの証明はユークリッドの証明よりも遥かに複雑ですが、級数などの解析学を整数論に用いることにより、解析的整数論(微積分学を用いた整数論)の幕が開きました。
グリゴリー・ペレルマンはポアンカレ予想を数学手法でなく物理分野で解いてしまいました。しかも100万ドルも数学のノーベル賞と言われるフィールズ賞も辞退しています。かっこよすぎませんか。
コラッツ予想も別分野でチャレンジすることにより新分野が開けるかもしれません。このたびのコラッツ予想解明への新手法は別分野(数学)でチャレンジしている最中に気づいたものです。
物理分野でチャレンジできればかっこいいですよ。まさに数学は発明か発見かです。
1.8 自己紹介
執筆者クリエータの素性が全くわからないのであれば記事の信頼にも関わりますので簡単ではありますが自己紹介させていただきます。
私は東京大学出身、同大学院で理学博士号を取得しました。専攻は光物性物理学でエンジニアとしまして富士通研究所、他メーカで実験と理論の両方をこなしてきました。理論解析では主に水晶振動子やフォトニック結晶などです。
偶然でありますが整数論の本を読み、この分野に興味を持つようになりました。そしてコラッツ予想という歴史的未解決問題に大変興味を抱くようになりました。整数論とは全く別の分野の本も数冊か読んでいまして、この知識が使えないかとコラッツ予想の解析に当てはめてみたわけです。
そしてコラッツ予想の定義と同値な命題を全く別分野で見い出しました。
リーマン予想とは目的とする所が違いますが
コラッツルールに従う全ての数字配列は、どんな初期値から出発してもCS空間ではCS直線式上に乗る
です。既にコラッツ予想に取り組んでいる方々には別分野の視点からという意味で大変参考になるはずです。
1.9 新手法の説明の前に
コラッツ予想のルール「奇数なら3倍して1を足す、偶数なら2で割る」におきまして、偶数は2で割っていくと必ず奇数に到達しますので、奇数のみを追っていき、偶数は特に断らない限り表記しないこととします。例えば1.1の13の例では、$${13 \to 5 \to 1}$$のように奇数のみ表記します。1に到達するまでの総ステップ数は$${\to}$$の総数で13の場合は総ステップ数=2と数えます。
$${No}$$を正奇数としまして、$${No=27}$$は数は小さいのに以下のように総ステップ数は41もあります。奇数のみ追っていて、最大数は3077です。

この奇数変化を横軸にステップ番号(27は番号0、1は番号41)
を、縦軸に各番号の奇数の値を表示したのが図1-2です。
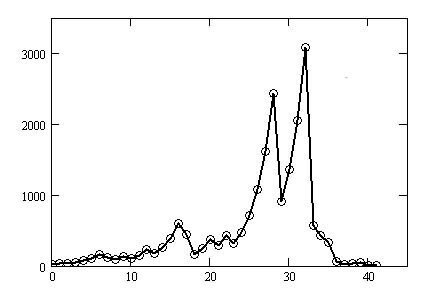
図1-2のグラフに新手法で変換を施すと図1-3となります。
CS振動 と呼ぶことにします。CはコラッツのCも兼ねています。
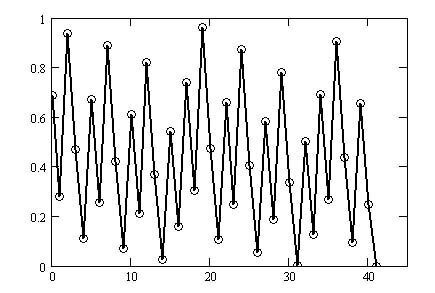
図1-3は図1-2に比べて規則性や周期性が見て取れます。この規則性はまだ序の口でして、さらに幾つか変換を施していきます。するとより一層明確な規則性が見えてきます。初期値が27以外でもステップ数の違いこそあれ同様の傾向が現れます。最終的には任意の正奇数$${No}$$について、この傾向を説明する一般式と命題を紹介します。
変数・定義語
$${N}$$、$${No}$$、
総ステップ数、ステップ番号、CS振動
第1章は新手法解析前の諸紹介ですが、記事内容で「なるほど」とお感じになったら、評価の程よろしくお願いいたします。今後の解析の奮起につながります。
(休憩室)創作いろは歌もぜひご覧ください。
1-10 第2章以降の記事について
新手法の記事は第1章(1記事目)から第8章(10記事目)ですが、
第6章6.1(7記事目)および6.2(8記事目)が新手法の解析のメイン記事です。第2章から第5章までに登場した用語・変数・導出式から第6章の弱い命題&強い命題は理解できます。
すべてまとめからとなりますと紹介も先になってしまいますので、逐次まとめながら紹介させていただきました。
記事として投稿説明することにより、内容が具合的になり例も多く盛り込むことができ理解しやすくなります。これが論文ですと内容が凝縮してしまって、形式にもこだわることになり、理解に時間を費やすことになります。
本質的な箇所をぜひつかんでコラッツ予想解析のヒントにしていってください。
各章の記事ではキーとなる内容は途中で有料記事とさせていただきました。またキーとなる内容でなくても、章の中のセクションでも有料記事となる場合もあります。後者の場合は全てではありませんが式の導出証明などです。
次の記事は第2章(2.1&2.2)ですが、一般正奇数$${\bm{No}}$$でCS振動の導出方法とCS振動のさらなる変換の紹介、および、No=27を例にとった変換特性説明で2.2は有料記事とさせていただきました。冒頭のリンクにある要約動画、および無料記事、途中まで無料記事の箇所もご判断の大変参考になります。
休憩室(創作いろは歌)
広く知っていただきたい
七五調富士山いろは歌
および
中学高校受験生のための合格必勝いろは歌




必勝4月目標達成カード
A1. 現代いろは歌について
短歌は五七五七七の31文字、俳句は五七五の17文字で作られた日本の古来からある歌で一般の方々も作り新聞にもよく掲載されています。現在は短歌ブームとも言われています。
いろは歌も「いろはにほへと」で始まる旧仮名使用の元祖いろは歌があり1000年の歴史がある由緒ある歌ですが、そのルールの厳しさから現代いろは歌は広く普及には至っておりません。また元祖いろは歌は知っていても、ルールまでは知らない人は結構おります。
そのルールは「ひらがな46文字全てを使用し、しかも1文字1回のみ使用」というルールです。ひらがなは50音といわれますが、現代ひらがなは、「あ」から「ん」まで46文字あります。言い換えますと、いろは歌をひらがなのみで表し「あ、い、う」と順番に探してはチェックを入れていきますと最後に「ん」で終了します。
A2. 七五調富士山いろは歌について(図a1)
七五調富士山いろは歌は故人である父が元気なころに創作した歌で、当時日本経済新聞(日経)や旺文社蛍雪時代月刊誌で連載、TV等々でも紹介されました。
創作者は日経でも「創作には理系の頭脳も必要」と述べています。確かにひらがな46文字を並べ替えて歌を創作するわけですから、パズル的要素もあります。創作難易度は短歌・俳句を遥かに凌駕します。
七五調富士山いろは歌はいろは歌ルールに加え、短歌・俳句のルールでもある、更に七音と五音で作られており、到底真似できる歌ではありません。歌の内容も大変綺麗です(図a5)。

A3. 合格必勝いろは歌について(図a2,図a3、図a4)
合格必勝いろは歌はタイトル必勝いろは歌(図a2、図a3)と中学高校受験生のための各月計12種合格必勝いろは歌(図a4)があります。
タイトル必勝いろは歌は合格を含めた必勝を願う全ての人に共通する歌です。
中学高校受験生のこよみは4月から始まります。
各月合格必勝いろは歌は4月から3月までの計12種ありまして、その内の合格必勝4月を一例としまして図a4に示しました。使い方は図a6に説明しましたが、各月目標達成カードとしました。
各月合格必勝いろは歌には月名と季語相当語句(例:四月、春)が含まれ
12種すべてが現代いろは歌ルールに従っており、こちらも到底真似できる歌ではありません。
ポストカードとしても使えるようにしました。各月の目標を書いて勉強室に一か月飾る、もしくは各月のアドバイスやメッセージを両親・先生・友人・先輩方が書いて送ることもできます。
奮起継続には手書きが一番
と考えております。両親から離れて上京して勤しんでいる学生さん達には特に励みになると考えます。

