スプライン曲線による補間（出発点）

2018年7月13日 15:45

出発点は検索すれば出てくるものの焼き直しです。ただし自分が分かりやすいように書き直しています。

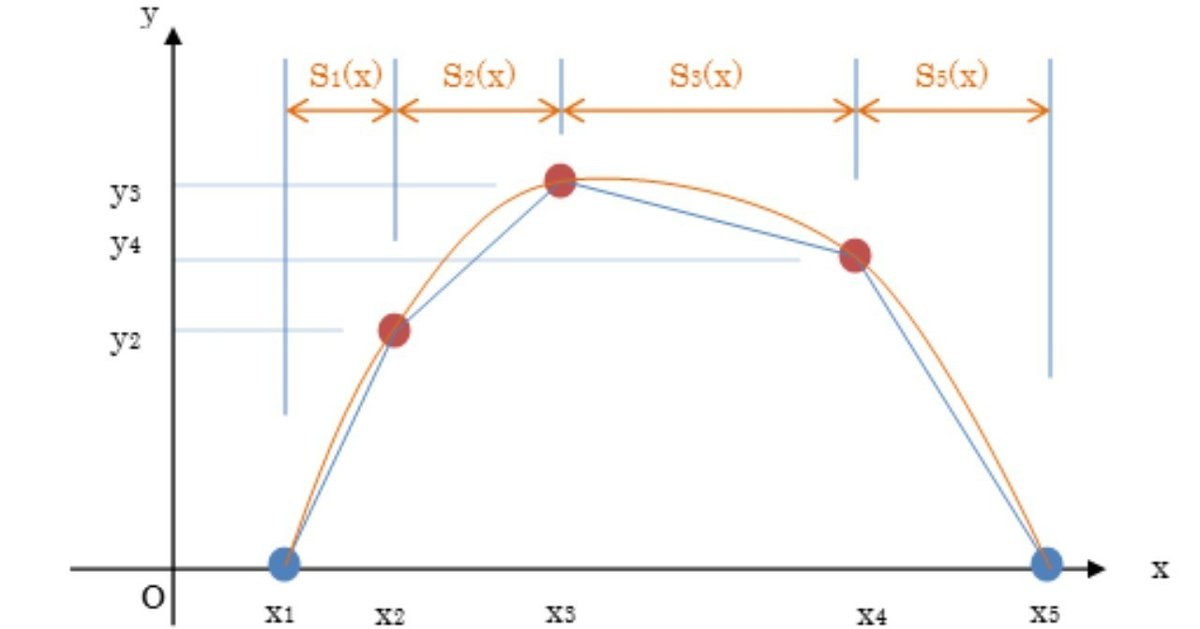
いまx-y平面に(x1,y1),・・・,(xN,yN)のN点があるとする。( xj+1 > xj )
ここではスプライン曲線S(x)は(xj,yj)を始点とする多項式Sj(x)を持つ区分関数とし、

であるとする。
この関数S(x)は
１．すべての選点を通る。
２．すべての選点において隣接する関数の微分値が一致する。
３．すべての選点において隣接する関数の2回微分値が一致する。
これらを満たすものとする。
また区間距離をhj、選点差分をrjとする。

Sj(x)に対して選点における2次導関数の値ujは

よってbjは

次に選点で隣接する2次導関数の値は等しいので

よってajは

次に選点に隣接する関数値は選点で既知なので

区分区間の終点においては

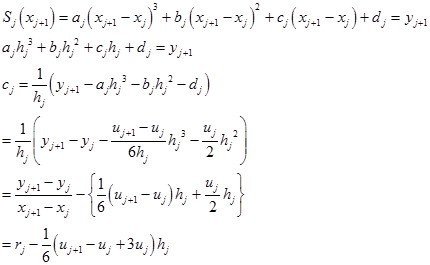
よってcjは

係数をまとめると

である。
1次導関数は

1次導関数は選点において等しいから

係数はujを用いて表すと

したがってある選点の前後の区間で考えると

ここで両端の2次導関数の値u1, uNを0とすると

がN-2元1次連立方程式を成し、ujを解いて関数S(x)を得る。
このとき両端(x1,y1),(xN,yN)は変曲点である。

自分のノートを手抜きでコピペしてみましたが、
画像はぼやける。数式も(画像なので)ぼやける。
行間は広い。添え字ができない。
と、たぶん読みにくいと思います。
なので無料公開分については別サイトにPDFを置き、
有料分についてはPDFのDLもあわせたやり方がいいかなと思案中です。

言葉や表記が自己流だったり揺らぎがあったりします。
ほんとひっで
ゆるして

いいなと思ったら応援しよう！