
いい証明を思いついた①〈角の二等分線〉
命題
三角形ABCにおいて、角Aの二等分線が辺BCと交わる点をDとする。AB = a、AC = b、BD = c、CD = d とするとき、a : b = c : d である。

これは、角の二等分線というシンプルな仮定だけで、a : b = c : d という印象的な式をみちびく、美しい命題だ。
一般的な証明
この命題の、一般的な証明は以下の通り。(読まなくてもよい。)
点Cから線分ADに平行な直線を引き、直線ABとの交点をEとすると、平行線の公準より、三角形ACEは二等辺三角形となることがわかる。
よって、AE = AC = b 。

ここで三角形ABDと三角形EBCに注目すると、AD // EC より、これらは相似であることがわかる。よって、a : b = c : d 。(終)
確かに a : b = c : d であることは証明された。
しかし、この証明からは、なぜ a : b = c : d になるのかという肝心な部分、命題の気持ち、がわからない。
つまり、これらの辺の比は、もっと根本的なもので結びついているはずなのに、三角形が外側に拡張されてしまったせいで、それが見えてこないのだ。
もっとすっきりした証明があるはずだ。角の二等分線の性質を上手に用いた、もっとシンプルな証明が。
ひらめき
あるとき私は、この図の下半分に注目していた。角の二等分線ばかりに注目していても、まったく埒があかない、と思ったからである。

そのとき、ある考えがよぎる。
「これは、面積...比!」
底辺の分割比 c : d は、左右の三角形の面積比であることに気がついたのだ。
頂点Aを共有する2つの三角形は、高さが共通のため、面積比は底辺の長さ比となる。基本の基本だが、角の二等分線に気を取られていて、気づかなかった。
思いついた証明
ここから、一気に証明が完成する。
点Dから辺AB、ACに垂線を下ろし、その足をそれぞれF、Gとする。直角三角形AFDと直角三角形AGDは、斜辺と一つの鋭角が等しいので、合同である。
よって、FD = GD 。
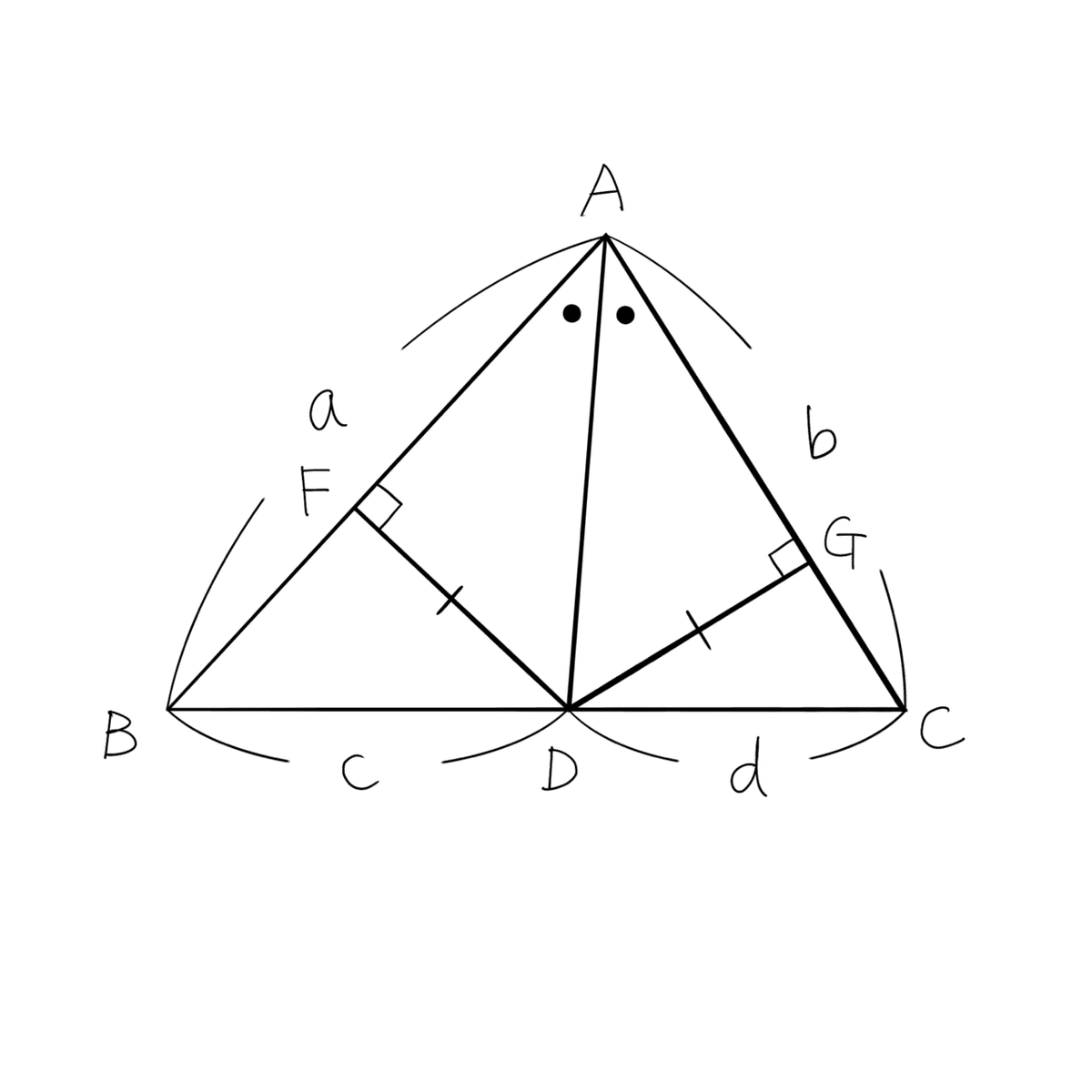
ここで、辺AB、ACを底辺とみなすと、三角形ABDと三角形ACDの面積比は、a : b である。一方、辺BD、CDを底辺とみなすと、これらの三角形の面積比は c : d となる。よって、a : b = c : d である。(終)
なるほど! 美しい辺の比は、面積比で結びついていたのだ。
「角の二等分線上からそれぞれの辺に垂線を下ろすと、どちらも同じ長さになる」という性質を用いているのもポイントだ。
これなら理解しやすいし、覚えやすい。
いい証明を、思いついた。
