
エクセル分析スペシャリスト対策 #05 - 相関分析・回帰分析の手法
今回は相関分析・回帰分析について学んでいきたいと思います。
分散のF検定と平均値のt検定・一元配置分散分析は質的変数と量的変数の関係を検定する方法でしたが、今回の相関分析・回帰分析は量的変数と量的変数の比較を行うことができます。
量的変数と量的変数の関係については、次の2つのケースを考えます。
1、原因系・結果系の関係にない場合を想定(相関関係)
例. 商品Aを購入する人は商品Bも購入する傾向がある(因果関係ではなく、双方向の関係)
→無相関検定
2、原因→結果の因果関係を想定(回帰分析)
例.性別ごとに商品A・商品Bの売りあげが有意に異なる(性別:原因、商品売り上げ:結果という因果関係を想定)
→回帰の有意性の検定
1、原因系・結果系の関係にない場合を想定した検定(相関分析、無相関検定)
原因系・結果系の関係にないデータに相関があるかを検定するには、相関分析を行います。相関分析を行うには散布図に各データの近似曲線を描く他、相関係数を算出する方法があります。

相関係数を算出するにはデータ分析で複数データの相関係数を表示できる他、CORREL()関数で直接値を算出することができます。相関係数の目安としては、一般に次の基準で言語化します。
0.7 - 1.0:強い相関あり
0.4 - 0.7:やや相関あ
0.2 - 0.4:弱い相関あり
0.0 - 0.2:ほぼ相関なし
相関係数に関しては、標本集団の相関係数・自由度を使った値がt分布に従うことが分かっています。これを利用して、母集団の相関係数が0と仮定した無相関検定を行うことができます。無相関検定の結果は、標本では相関がある場合に母集団でも同様に相関があるかどうかを検定できます。
2データの相関係数のt値の絶対値・自由度は、以下の式で計算します。
t値の絶対値:相関係数 * √(データ数 - 2) / √(1 - 相関係数^2)
自由度:(データ数 - 2)
求めたt値を有意確率(P値)に戻すには、TDIST()関数を使います。

相関係数の算出では商品の好みの双方の関係性を検討することができますが、どちらが原因となって需要を高めているかという因果関係の検定には使えません。
2、原因→結果の因果関係を想定した検定(回帰分析、回帰の有意性の検定)
原因系・結果系の関係にあるかを検定するには、回帰分析を行います。
最初にスマホ利用者の利用期間・満足度の散布図を描き、近似曲線を描く場合を考えます。
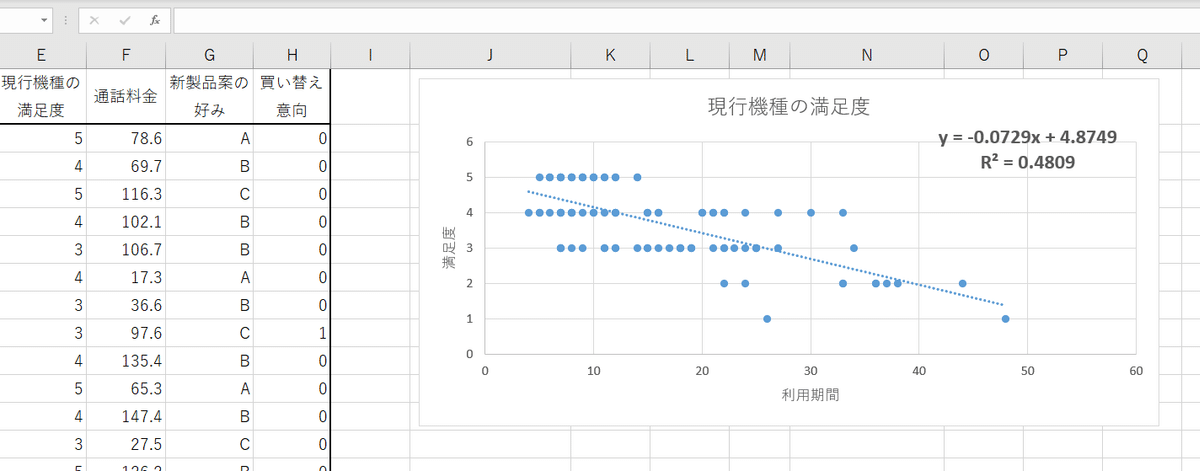
今回はまず、近似曲線が1次曲線である場合を考えます。1次曲線の傾きと切片は、原因系と結果系の因果関係がどのような値かを表現できます。
また、この近似曲線がどのくらい実測値に即しているかを決定係数(R2)で表せます。決定係数は予測値が全く正確でない場合は0以下、逆に精度が高いほど1に近い値を取ります。

単回帰分析(説明変数が1つ)の場合は、t検定で回帰分析の結果が有意か(傾き=0を帰無仮説とする)を検定できます。重回帰分析(説明変数が2つ以上)の場合は、F検定で傾きの有意性を検定できます。これを回帰の有意性の検定と言います。Excelではデータ分析を行えば決定係数の傾き・切片の値の回帰の有意性の検定ができます。
説明変数に質的変数が含まれる場合は、質的変数をダミー変数=量的変数に変換し、その数値を回帰分析することができます。


