
目指せ!ES#007:初歩のフィルタ
身の回りにあふれている「フィルター」

複数のものが混ざっている状態から「欲しいもの」と「いらないもの」に選り分けてくれる(=ろ過する)役割を果たすのが「フィルター」です.
普段あまり意識しないかもしれませんが,私たちの身の回りには「フィルター」がたくさんあります.
上の写真のようにコーヒーの抽出に使う「コーヒーフィルター」はコーヒー粉とコーヒーの混合物からコーヒーだけを取り出す役割を果たしますし,エアコンなどに内蔵されている「エアフィルター」は空気中のホコリや塵を取り除いて,きれいな空気だけを取り出します.
フィルターと名前がつくものだけではありません.例えば「網戸」は部屋の外から風を取り込みつつ蚊の侵入を防ぎます.茶こしはお茶と茶葉を分離します.
交差点に設置されている「信号機」も,放っておくと直進やら右折やら好き勝手動く車や歩行者を「進んでよい車・人」と「止まらなければいけない車・人」に分離しているという意味ではフィルタと言えるかもしれません.
ですが,本稿で説明するのは「電気信号のフィルター」(フィルター回路)です.
フィルター回路は何をろ過するのか

電気信号はいろいろな成分が「混ざりあって」できている
下のグラフは,私の声をマイクで録音した波形です.低いラの音(110[Hz])を狙って出しました.大体0.09[sec]周期で同じ形が繰り返されています.これを周波数に換算すると,狙い通りの音程になっていることがわかります.
$$
f=\frac{1}{0.09\mathrm{[sec]}}=110\mathrm{[Hz]}
$$

しかしこの波形,110[Hz]の正弦波とは似ても似つかない形です.

一定周期Tで同じ形を繰り返している(周期波形)が,形が正弦波でないという信号は,周期Tに対応する基本周波数f0の正弦波と,その整数倍の正弦波が混ざり合ってできています.上図に示した私の声の場合,周期0.09[sec]ですので基本周波数f0は110「Hz],さらにその整数倍の成分が混ざり合っています.
高速フーリエ変換(FFT)という処理を行うと,周期波形を構成している周波数成分を分解して見ることができます.上図に示した私の声を分解すると,f0=約110[Hz],f1=約220[Hz],f3=約330[Hz]…に大きなピークがあり,確かに基本周波数の整数倍成分が集まっていることがわかります.

さらに詳しく学びたい人は,別ページで私が連載している「イメージでしっかりつかむ信号処理〜基礎から学ぶFFT〜【準備編1:信号とは】」をご覧ください.
とりあえずここでは「世の中の信号は多数の正弦波が混ざってできている」ということだけ理解して頂ければよいです.
フィルター回路は不要な周波数成分を取り除く
「電気信号のフィルター」(フィルター回路)は何をろ過するのかというと,「信号の中の不要な周波数成分」をろ過する(取り除く)働きを持ちます.「周波数フィルタ」という呼び方をすることもあります.
周波数フィルタには,どの周波数帯域を取り出すか(取り除くか)で大きく4つの種類があります.特にローパスフィルタとハイパスフィルタは基本中の基本フィルタとして重要です.

フィルタ回路の実現方法

LPF,HPF,BPF,BEFというのはフィルタの「機能」であって,実現方法は様々です.中でも抵抗(R)とコンデンサ(C)を組み合わせて作るRCのLPF,HPFフィルタは,周波数特性(各周波数ごとにどの程度減衰するか)が緩やかですが,構造が簡単で手軽に作れるため,よく使われます.
RC LPFとRC HPF
抵抗とコンデンサを一つずつ使うと,(一次の)LPFとHPFが作れます.

2つの回路がどのように働くのかを,回路シミュレータを使用してみてみましょう.Falstadというフリーのオンライン回路シミュレータを使用しています.
まずはフィルタ回路を入れない状態のシミュレーション結果を示します.入力信号は20~2000[Hz]まで周波数が連続的に変化するスイープ正弦波です.信号に影響を与える回路が何もないため,出力信号には入力信号がそのまま見えています.

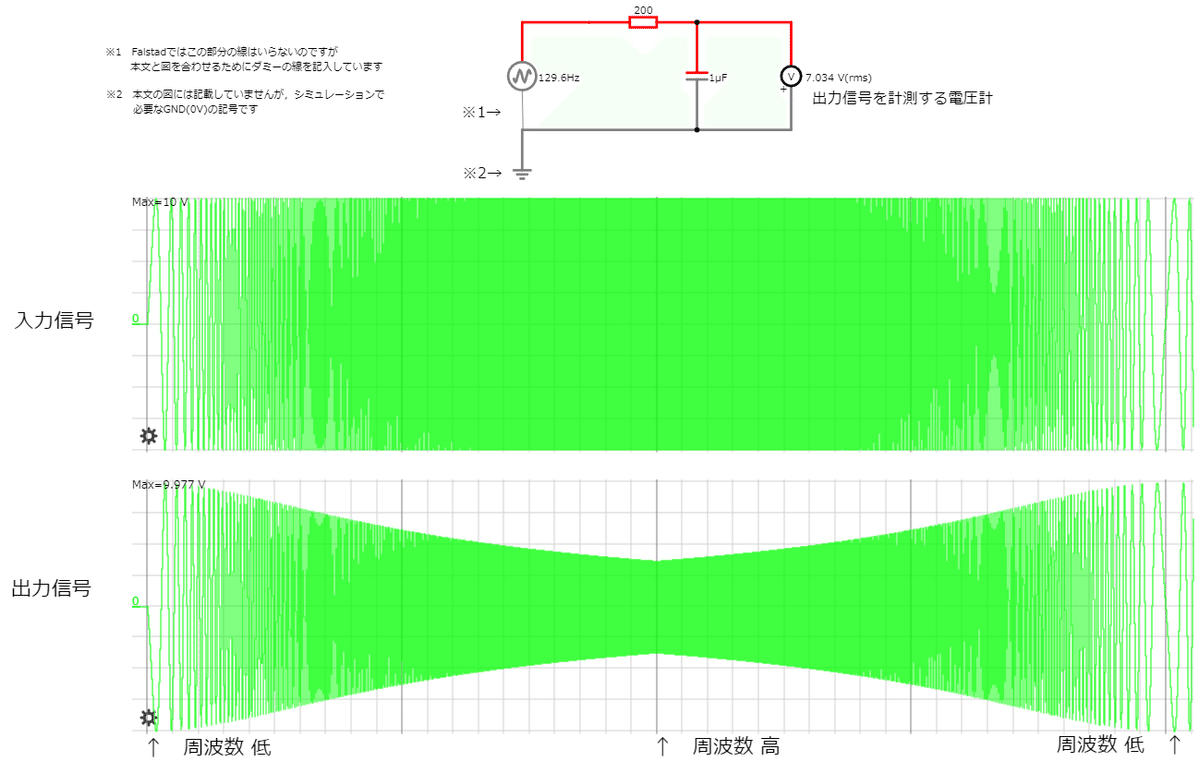
では,入力信号の後ろにRC LPF回路を挿入します.抵抗Rは200[Ω],コンデンサCは1[μF]に設定しています.両端の低周波部分ではほぼ入力信号がそのまま出力(=ロー【低周波】がパス【通過】)されているのに対し,中央の高周波部分では出力信号が小さくなっていることがわかります.入力信号は±10[V]であるのに対し,中央のもっとも出力信号が小さくなった部分は3.7[V]しかありません.
これは,低周波(直流または直流に近い)では電流がコンデンサを通過できずにほぼそのまま電圧として見えているのに対し,高周波では電流がコンデンサを通るようになるため,出力信号を計測している電圧計に到達する前にコンデンサを通じてエネルギーが逃げてしまう事で起こります.
次に,抵抗とコンデンサの値はそのままに,位置を入れ替えてみます.これはRC HPF回路になります.先ほどとは逆に両端の低周波部分では出力信号がとても小さいのに対し,中央の高周波部分ではほぼ入力信号がそのまま出力(=ハイ【高周波】がパス【通過】)されていることがわかります.ただし最大周波数がまだ十分高くないため,中央の最高周波数部分でも入力電圧の±10[V]には足りず,約9.3[V]です.
これは,低周波(直流または直流に近い)では電流がコンデンサを通過できずエネルギーが出ていかないのに対し,高周波では電流がコンデンサを通るようになって出力側にエネルギーが供給されるようになる事で起こります.

また同じフィルタ回路でも,CとRの値を変えれば特性が変化します.下の図は,回路はHPFのままでCの値を先ほどの半分(500[nF])に変えてみたものです.
低周波の信号がより通りにくくなり,中心の最高周波数部分でも約7.8[V]しかありません.

フィルタ回路の応用
ローパスフィルタを使う事で,バタバタ激しく変化するPWM信号を,なめらかなアナログ信号に変換することができます.
以下の図は,マイコンが出力するPWM信号を再現したキャリア周波数1[kHz],最大電圧3.3[V]のパルス波を,Rが250[Ω],Cが20[μF]のRC LPFに通したシミュレーション結果です.多少の変動が残り,入力信号の変化に対して出力信号の変化が遅れてはいますが,入力信号に比べるとずっと滑らかな電圧変化をしていることがわかります.

執筆者
N.Y.City(山口直彦)
工学院大学学生職員、組み込みエンジニア、専門学校HAL東京(先端ロボット開発学科)教員を経て、現在東京国際工科専門職大学(情報工学科)助手。プログラムや電子回路、産業用ロボット教育等に従事。その他、音楽情報科学研究、文筆業、ラノベ研究や発達障害者支援、写真等も。
主要著書
『コンピュータの動くしくみ(電子書籍再刊)』(秀和システム,2019年)
『小説の生存戦略 ライトノベル・メディア・ジェンダー』(青弓社,2020年)
Web連載「イメージでしっかりつかむ信号処理」(APS-WEB,2023~)
より詳細なプロフィールはWeb(N.Y.Cityのまちかど)へ。
