
NIRSの信号処理について考えてみる〜③フーリエ変換〜
前回フーリエ変換についてちょっと触れたけど,今回はもう少しだけ踏み込んでみる。
「フーリエ変換」は聞いたことあるけど結局何をしているのかがわからない人向けに,具体的に何をするのかについて一切数式を使わずにざっくりと,それはもうざっくりとまとめてみる。
あくまで心理学の領域にいる(不本意だけど文系に分類される領域の)人間の理解の範疇の内容なので,専門の人から見たら基本的なことしか扱っていない&厳密なこととは違っているだろうけどお気になさらず。
フーリエ変換ってなんぞや
「あらゆる波は三角関数の和で表すことができるということを利用して,波を周波数ごとに分解する」というイメージ。つまりこんな感じ(図1)。

いやいや待てと。本当に三角関数の和で何でも表せるのかと。という疑問を持つ人もいると思う。
そんな方にはこちらの動画がおすすめ。
「YouTube【物理エンジン】円板の組み合わせだけで何でも描けるフーリエ変換の話 Fourier transform」
NIRSデータだと,脳の応答成分が含まれているかどうかの確認や,フィルタを作成する際に遮断周波数を何Hzにするのか,作成したフィルタがノイズを適切に減衰させたかなどを確認するためにも,手元のデータの周波数成分を調べる必要がある。
MATLAB上でフーリエ変換を実装する方法は前回の記事に書いてあるからここでは省略する。
ただ,前回のコードの中に「窓関数」というものがあったけど,これについて触れていなかったからここで説明をする。
そもそもフーリエ変換は連続する波に適用するという前提があるとのこと
(手元にある波と全く同じものが前後に連続的に限りなく続いているという感じ)。
だから連続しない波に適用すると結果が歪んでしまう。
NIRSデータで言えば,一定の時間幅で取得したものが周期的な波形であることなんてまずないだろうから,手元のデータにそのままフーリエ変換を適用するのは不適切だということ。
サンプルデータで見てみよう。フーリエ変換の前提に則るなら前後に同じ波形が続かないといけないことになるけど,実際はそんなことにはまずならない。360秒–0秒の部分は連続していないことがよくわかる(図2)。

窓関数
上のような不連続性を補正するために「窓関数」を使う。
簡単に言えば,手元のデータの両端を0にして連続するものとみなすために使うもの。
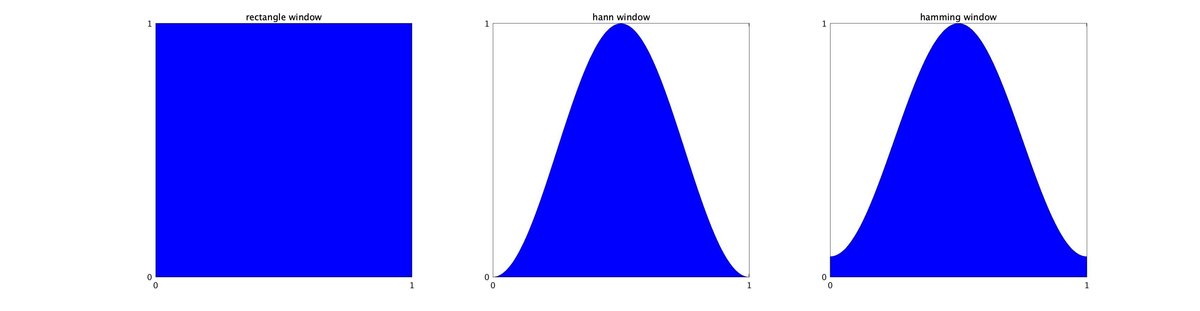
窓関数にも色々あるけど,多くの場合は「ハン窓」か「ハミング窓」が使われるとのことで(「ハミング窓」に合わせて「ハン窓」は「ハニング窓」とも呼ばれる)。
これらの窓関数の形はこんな感じ(図3)。実際にはこの関数を手元のデータに畳み込むので,サンプルデータに合わせて横軸を0–360とした。

ハン窓は両端を0にして連続性を確保する分,この辺りにある波形の変化(周波数成分の存在)を見落としてしまう可能性がある。それを改善するために,連続性を多少犠牲にして周波数分解能(周波数の検出性能)を上げたものがハミング窓だそうで。
ちなみにMATLABの関数"fft"でフーリエ変換をする際に窓関数の設定をしない場合は,窓関数を使っていないと思いきや実は矩形窓(全ての時間で1となる関数…というかxy座標でいうところのy = 1 (0 ≦ x ≦ t)の直線)を使っていることになるというね。結果だけ見れば何もしていないのと同じだけど(元のデータに1を掛けるだけだからね)。
窓関数による振幅の減衰
フーリエ変換するなら窓関数も考えてねという話だったけど,窓関数を畳み込むと元のデータの振幅が小さくなってしまう(矩形窓は別として)。
ACF (Amplitude Correction Factor)を使ってこれを補正するわけなんだけど,イメージとしては窓関数の面積に応じて振幅が小さくなるからその分を元に戻すという感じ。
窓関数を使わない=矩形窓の面積を1とすると,ハン窓の面積は0.5,ハミング窓の面積は約0.54なので,ハン窓を使った場合は変換後の振幅を2倍すればいいし,ハミング窓を使った場合は変換後の振幅を約1.85倍すればいい(図4)。窓の面積の逆数をACFとして変換後のデータに掛けていることになるのかな。
厳密には違うのだろうけど,こんなことをしているんだよ程度の理解はしておきたい今日この頃。
窓あり窓なし補正あり補正なしの比較
というわけで,サンプルデータ(図2とは違うけど)を使って,元々の波形と窓関数を畳み込んだ場合の波形,およびそれぞれのフーリエ変換の結果と振幅補正の有無の比較を図にしてみた(図5)。

(補正後の振幅が窓なしと一致していない(特に上段)のは何が原因なんだろう?各パラメータにミスはないはずなんだけど…)
まとめ
どんな周波数の波が含まれているのかを調べるためにフーリエ変換します。
波は連続することが前提なので,それを満たすために窓関数を使います。
窓関数を使うと振幅が小さくなるのでこれを補正します。
といった感じかな。
次回はフーリエ変換の限界と「じゃあどうしたらいいよのさ」について書こうと思う。
最後に,フーリエ変換についてもっと専門的なことをわかりやすく解説している動画があったので,それを紹介して今回は終わります。
「YouTube【3Blue1BrownJapan】【視覚的に理解する】フーリエ変換」
