資金600万から資産1億円に到達する方法（その2、短期的なマイナスは織り込もう、資産推移の分布は逆正弦定理に従う）

2024年2月12日 13:16

知人から「600万円貯金ができたけどどうしたら良いかな？1億円目指してFIREしたいんだけど。やっぱ個別株をタイミング見て買うのが良いかな？」、と相談を受けた、という前提でどのようにすれば資産1億円（いわゆる億り人）になれるか、というのを考えていきます。自分の思い込みではなく、数学的な背景、前提をもとにPythonでシミュレーションをしていきます。結論から言うとインデックス投資一択です、あと株価は忘れて本業に集中です。その理由を解説してきます。

今回は投資を始めたら資産がマイナスになり嫌になって投資をやめてしまう、というのが往々にありそれについて解説してみます。

なぜ投資初期に元本割れを起こすのか？

”投資したらすぐに下がって怖くなって売ってしまった、それ以来投資してないんですよ”、みたいなことを聞きます。この現象について考えてみます。

Q. 確率50％で当たれば1万円増える、逆に外れると1万円減るというゲームを考えます。このときに600万円からはじめて1億円に到達することを目指します、このときに一度でも元本割れする可能性は何％でしょうか？また元本割れするとしたらゲームを初めて何回目が一番多いでしょうか？

この問題は理論値が求まります、元本割れ、というのは資金1万円で開始して1億円に到達する前に破産する可能性と同じですから

$$
P_{ruin}(I) ={1- \frac{I}{T}}
$$

に当てはめると99.99%の確率で元本割れします。また勝率が60％の場合元本割れを許容すると下記公式より

$$
P_{\text{reach}}(I) = \frac{1 - \left(\frac{q}{p}\right)^I}{1 - \left(\frac{q}{p}\right)^T}
$$

ほぼ100％の可能性で資産1億円を達成できますが、元本割れを許容しない場合は66.7％の可能性で投資を終了することになります。

実際にPythonでシミュレーションしてみます、600万から開始して元本割れし投資を終了するまでの回数を求めると平均で4.2回目、中央値では1回目と非常に投資を始めた早期に元本割れを起こすことがわかります。

import matplotlib.pyplot as plt
import numpy as np

# シミュレーションのパラメータ
initial_capital = 6000000  # 初期資金: 600万円
target_capital = 100000000  # 目標金額: 1億円
change_per_toss = 10000  # コイントスごとの増減額: 1万円
n_simulations = 1000  # シミュレーションの回数
p_heads = 0.60  # 表が出る確率（1万円増える確率）

# 元本割れするまでの施行回数を記録するリスト
tosses_until_breach = []

# シミュレーションの実行
for sim in range(n_simulations):
    capital = initial_capital
    toss_count = 0
    while capital < target_capital and capital >= initial_capital:
        toss_result = np.random.choice(["up", "down"], p=[p_heads, 1-p_heads])
        capital += change_per_toss if toss_result == "up" else -change_per_toss
        toss_count += 1
        if capital < initial_capital:
            tosses_until_breach.append(toss_count)
            break

# 元本割れするまでの施行回数の頻度を計算
tosses_freq = {}
for tosses in tosses_until_breach:
    if tosses in tosses_freq:
        tosses_freq[tosses] += 1
    else:
        tosses_freq[tosses] = 1

# 棒グラフで表示
plt.bar(tosses_freq.keys(), tosses_freq.values())
plt.xlabel('Tosses Until Capital Breach')
plt.ylabel('Frequency')
plt.title('Frequency of Tosses Until Capital Breach')
plt.show()

# 元本割れする確率の計算
breach_probability = len(tosses_until_breach) / n_simulations

# 元本割れするまでの回数の平均値と中央値の計算
if tosses_until_breach:
    average_breach_tosses = np.mean(tosses_until_breach)
    median_breach_tosses = np.median(tosses_until_breach)
else:
    average_breach_tosses = 0
    median_breach_tosses = 0

breach_probability, average_breach_tosses, median_breach_tosses

これらのことから導けるメッセージは
"どんなに良い投資でも初期の元本割れは許容しないといけない”
ということかとでしょう。特に投資を始めた初期は高率に元本割れします。

資産推移は逆正弦定理に従う

”逆正弦定理”とは何がいいたいのかわかりにくいのですが最初に元本割れするとなかなかもどらないことが多い、という現象です。

コイントスで考える

次のようなシミュレーションを考えます。
”偏りのないコインを1枚用意する。コインを投げて表が出たら勝ち、裏が出たら負けとする。勝ちの場合は100円を受け取り、負けの場合は100円を支払う。このコイン投げを何度も繰り返す。コインを投げるごとに、100円を受け取ったり支払ったりするので収支が変動する。これを10回繰り返す。”

1000回繰り返して最終的な収支の分布を棒グラフにしてみます。

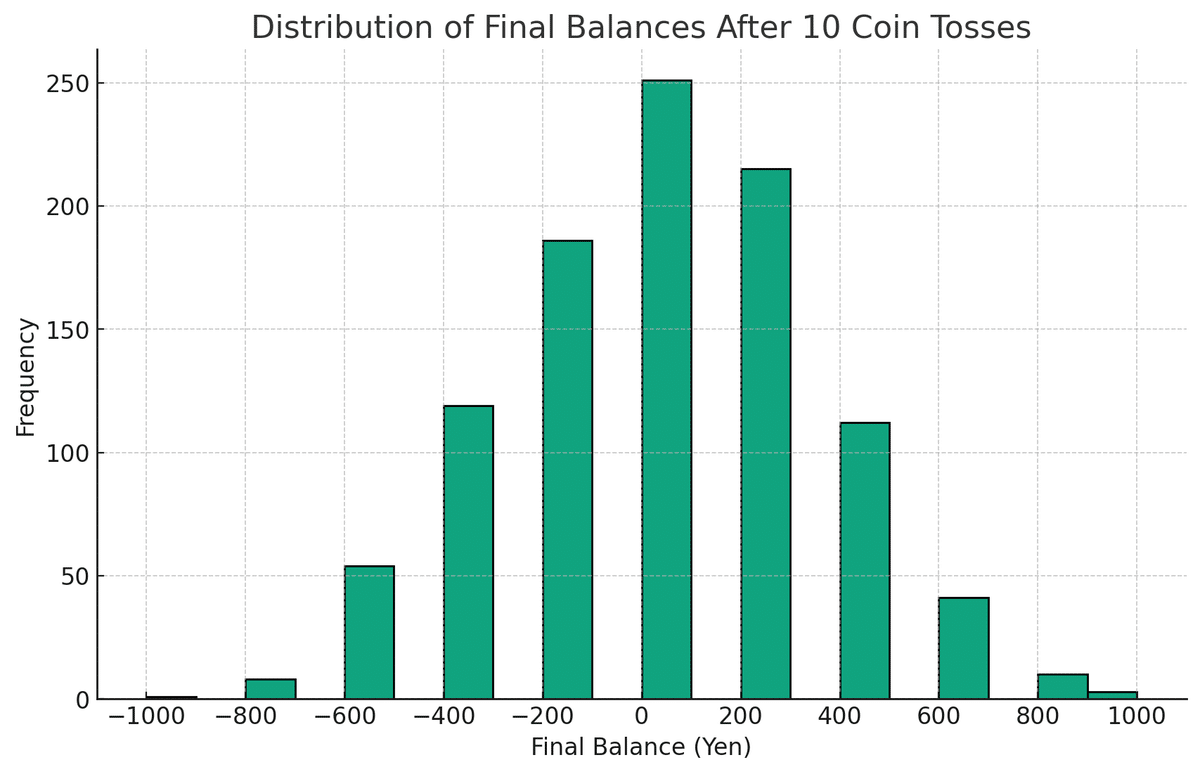
import matplotlib.pyplot as plt
import random

# コイン投げのシミュレーション関数
def coin_toss(n):
    balance = 0
    for _ in range(n):
        toss = random.choice(["heads", "tails"])
        if toss == "heads":
            balance += 100
        else:
            balance -= 100
    return balance

# シミュレーションを複数回実行し、収支の分布を取得
n_tosses = 10
n_simulations = 1000
final_balances = [coin_toss(n_tosses) for _ in range(n_simulations)]

# 収支の分布をヒストグラムで表示
plt.hist(final_balances, bins=range(-1000, 1100, 100), edgecolor='black')
plt.xlabel('Final Balance (Yen)')
plt.ylabel('Frequency')
plt.title('Distribution of Final Balances After 10 Coin Tosses')
plt.xticks(range(-1000, 1100, 200))
plt.show()

当然ながら上記のグラフは二項分布に従い、また期待値は勝率50％ですから0になります。

次に収支を時間軸について表すグラフを描いてみます、これも1000回繰り返しますので頻度が高いところは濃く、低いところは薄くなります。

import numpy as np

# コイン投げのシミュレーション関数（累計収支を追跡）
def coin_toss_tracking(n):
    balances = [0]
    for _ in range(n):
        toss = random.choice(["heads", "tails"])
        new_balance = balances[-1] + 100 if toss == "heads" else balances[-1] - 100
        balances.append(new_balance)
    return balances

# シミュレーションを複数回実行し、各時点での収支の変動を記録
n_tosses = 10
n_simulations = 1000
all_balances = [coin_toss_tracking(n_tosses) for _ in range(n_simulations)]

# 各時点での収支を重ねてプロット
plt.figure(figsize=(10, 6))
for balances in all_balances:
    plt.plot(range(n_tosses + 1), balances, color='blue', linewidth=0.5, alpha=0.1)

plt.xlabel('Number of Tosses')
plt.ylabel('Balance (Yen)')
plt.title('Balance Over Time for 1000 Coin Toss Simulations')
plt.xticks(range(n_tosses + 1))
plt.axhline(y=0, color='black', linestyle='--')  # 中心線を追加
plt.show()

ここで収支の勝ち越し期間と負け越し期間について調べます、負け越し期間というのは元本割れしている期間です。直感的には勝ち越し期間、負け越し期間の分布は勝ち負け拮抗している±0を中心に分布しそうな気がしますが違います。

実際にシミュレーションしてみます。

from itertools import product

# 10回のコイントスのすべての可能な組み合わせを生成
combinations = list(product(["heads", "tails"], repeat=10))

def calculate_balance_difference(tosses):
    balance = 0
    positive_states = 0
    negative_states = 0

    for toss in tosses:
        balance += 100 if toss == "heads" else -100
        if balance > 0:
            positive_states += 1
        elif balance < 0:
            negative_states += 1

    return positive_states - negative_states

# すべての組み合わせについて、黒字と赤字の状態の差を計算
differences = [calculate_balance_difference(combination) for combination in combinations]

# 黒字と赤字の状態の差の分布をヒストグラムで表示
plt.hist(differences, bins=range(-11, 12), edgecolor='black', align='mid')
plt.xlabel('Positive States - Negative States')
plt.ylabel('Frequency')
plt.title('Distribution of State Differences After 10 Coin Tosses')
plt.xticks(range(-10, 11))
plt.show()

これはp=0.6（勝率60％）と変更しても同じです。

import matplotlib.pyplot as plt
import random

# 偏りのあるコイン投げをシミュレートする関数（勝つ確率が60％）
def biased_coin_toss(p_heads=0.6):
    return "heads" if random.random() < p_heads else "tails"

# コイントスの結果に基づいて、黒字と赤字の状態の差を計算する関数
def calculate_balance_difference(tosses):
    balance = 0
    positive_states = 0
    negative_states = 0

    for toss in tosses:
        balance += 100 if toss == "heads" else -100
        if balance > 0:
            positive_states += 1
        elif balance < 0:
            negative_states += 1

    return positive_states - negative_states

# 偏りのあるコイン投げのシミュレーション（1024回）
biased_combinations = [[biased_coin_toss() for _ in range(10)] for _ in range(1024)]

# 勝つ確率が60％の場合の黒字と赤字の状態の差を計算
biased_differences = [calculate_balance_difference(combination) for combination in biased_combinations]

# 勝つ確率が60％の場合の黒字と赤字の状態の差の分布をヒストグラムで表示
plt.hist(biased_differences, bins=range(-11, 12), edgecolor='black', align='mid')
plt.xlabel('Positive States - Negative States')
plt.ylabel('Frequency')
plt.title('Distribution of State Differences with 60% Winning Probability')
plt.xticks(range(-10, 11))
plt.show()

この勝ち越し期間、負け越し期間の分布は逆正弦定理という法則に従っています。実際の投資環境ではどのような現象として観察されるかというと"元本割れしてしまうとしばらく元本割れしている可能性が高い"という当たり前の現象です。しかし実際の投資では株価が下落すると反発を期待しておりそれが裏切られてなかなか元本復帰しないと投資自体をやめてしまうということをよくしがちです。多くの投資家にとって株価はランダムウォーク（幾何ブラウン運動）と同じ動きをします。投資初期の株価下落による元本割れはその後の反発をサポートするものではないというのを知っておく必要があります。この現象から学べるメッセージは”元本割れした場合はしばらく元本割れの期間が続くことが多いが投資は中断してはいけない”というメッセージかと思います。

続きはまた後日書きます。

この記事が気に入ったらサポートをしてみませんか？