資金600万から資産1億円に到達する方法(その5、S&P500を幾何ブラウン運動でモデル化してシミュレーション）

2024年3月20日 06:23

この記事では「600万円貯金があるけどどうしたら良いかな？1億円目指してFIREしたいんだけど。やっぱ個別株をタイミング見て買うのが良いかな？」、若い友人と相談を受けたという設定で最適な投資法を考えていくということが目的です。前回は株価のシミュレーションに用いられる幾何ブラウン運動についてその数式の導出や幾何ブラウン運動の性質について勉強しました。メッセージとして”株取引ではリスクはなるべく低いほうが良い”ということを述べたのですが今回は実際にS&P500の過去データを用いてシミュレーションしてみます。

株価変動を幾何ブラウン運動と考える

株価を幾何ブラウン運動でモデル化した場合、株価のリスクはボラティリティ（変動率）で表されます。幾何ブラウン運動を説明する下記の数式における$${\sigma}$$が株価変動のリスク＝ボラティリティとなります。

$$
dS_t = \mu S_t dt + \sigma S_t dW_t
$$

第一項は$${\mu}$$ (ドリフト項）であり単位時間あたりの株価の期待収益率を表します。通常は年単位ですので$${\mu=0.05}$$であれば株価は平均的に年率5％で成長すると期待されます。それに対して第二項、$${\sigma}$$(ボラティリティ項)は、株価の変動の大きさを表します。”私は安定よりもリスクをとって1億円を目指したい"と考えるかもしれません。幾何ブラウン運動でリスクを上げたらどうなるか考えていきます。

S&P500の過去データからドリフト項、ボラティリティ項を推定する

株式のモデルとしてはS&P500の過去データを使用します。S&P500の過去データはStooqから無料で入手可能です。S&P500のデータをダウンロード、そのデータを用いて解析を行います。

ドリフト項、ボラティリティ項は「Standard Cose to Close」法で推定しました。Google Colabｄでの解析方法はまずファイルを読み込ませます。

from google.colab import files

uploaded = files.upload()

次に解析を行います。過去20年間で解析してみます。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# データの読み込み
spx_data = pd.read_csv('/mnt/data/^spx_d.csv')

# Convert the 'Date' column to datetime format
spx_data['Date'] = pd.to_datetime(spx_data['Date'])

# Calculate daily logarithmic returns
spx_data['Log Returns'] = np.log(spx_data['Close'] / spx_data['Close'].shift(1))

# Extract the year from the 'Date' column for grouping
spx_data['Year'] = spx_data['Date'].dt.year

# Filter data for years 2004 and onwards
spx_data_filtered = spx_data[spx_data['Year'] >= 2004]

# Calculate the annual drift (mean) and volatility (standard deviation) of logarithmic returns
annual_metrics = spx_data_filtered.groupby('Year')['Log Returns'].agg(['mean', 'std']).dropna()

# Rename columns for clarity
annual_metrics.rename(columns={'mean': 'Annual Drift', 'std': 'Annual Volatility'}, inplace=True)

# Since we are working with annual metrics, multiply the mean by the number of trading days
# to annualize it. Assuming approximately 252 trading days in a year.
annual_metrics['Annual Drift'] *= 252
annual_metrics['Annual Volatility'] *= np.sqrt(252)

annual_metrics.reset_index(inplace=True)

# 年度別にテキストで出力
for index, row in annual_metrics.iterrows():
    print(f"{row['Year']}\t{row['Annual Drift']:.4f}\t{row['Annual Volatility']:.4f}")

# 平均値の出力
print(f"Average Annual Drift: {annual_metrics['Annual Drift'].mean():.4f}")
print(f"Average Annual Volatility: {annual_metrics['Annual Volatility'].mean():.4f}")

# Plotting
fig, ax1 = plt.subplots(figsize=(12, 6))

color = 'tab:red'
ax1.set_xlabel('Year')
ax1.set_ylabel('Annual Drift', color=color)
ax1.plot(annual_metrics['Year'], annual_metrics['Annual Drift'], color=color)
ax1.tick_params(axis='y', labelcolor=color)

ax2 = ax1.twinx()
color = 'tab:blue'
ax2.set_ylabel('Annual Volatility', color=color)
ax2.plot(annual_metrics['Year'], annual_metrics['Annual Volatility'], color=color)
ax2.tick_params(axis='y', labelcolor=color)

fig.tight_layout()
plt.title('Annual Drift and Volatility of SPX Log Returns (2004 Onwards)')
plt.show()

かなりばらつきが多いですが思い切って平均で考えてみます。2004年~2023年までの20年の平均ではμ(ドリフト項)=0.0730、σ(ボラティリティ項)=0.171となりました。本記事を書く際に参考にしたチャンドラ(@Chandra_11_11)さんのブログ記事ではS&P500のシミュレーションにはμ(ドリフト項)=0.07、σ(ボラティリティ項)=0.20がいつも使われています。今回もμ(ドリフト項)=0.07、σ(ボラティリティ項)=0.20でシミュレーションを行います。

S&P500を幾何ブラウン運動μ=0.07、σ=0.20でシミュレーションした場合に初期投資600万円が1億円になる可能性

S&P500にとりあえず全財産600万を入れて10年寝かせてみる、というプランです。1億円に到達する確率はどれくらいでしょうか？下記の式にμ=0.05、σ=0.20を当てはめてPythonでシミュレーションしてみます。同時に10年後に元本割れ（600万未満）している可能性も同時に求めてみましょう。

$$
dS_t = \mu S_t dt + \sigma S_t dW_t
$$

今回は1年間の取引日を252日にしております、シミュレーションは100,000回行ってます。1億円に生じた場合を青（5回分）、元本割れをした場合を赤線（100回分）、その他を緑線（100回分）描画しました。10年後の資産分布、平均値、中央値も求めてみます。

このシミュレーションでは1億円に到達する可能性は0.014％と極めて低いです。それに対して元本割れする可能性は21.2％と意外と高いことがわかります。期待値は1212万、中央値は991万でした。

シミュレーション期間を20年、30年と伸ばしてみます。

20年間のシミュレーション

20年間のシミュレーションでは1億円に到達する可能性は2.1％に上がりましたがまだまだ低いです。元本割れする可能性は13.2％と下がってきました。
資産分布の平均値は2439万円、中央値は1637万円となります。

30年間のシミュレーション

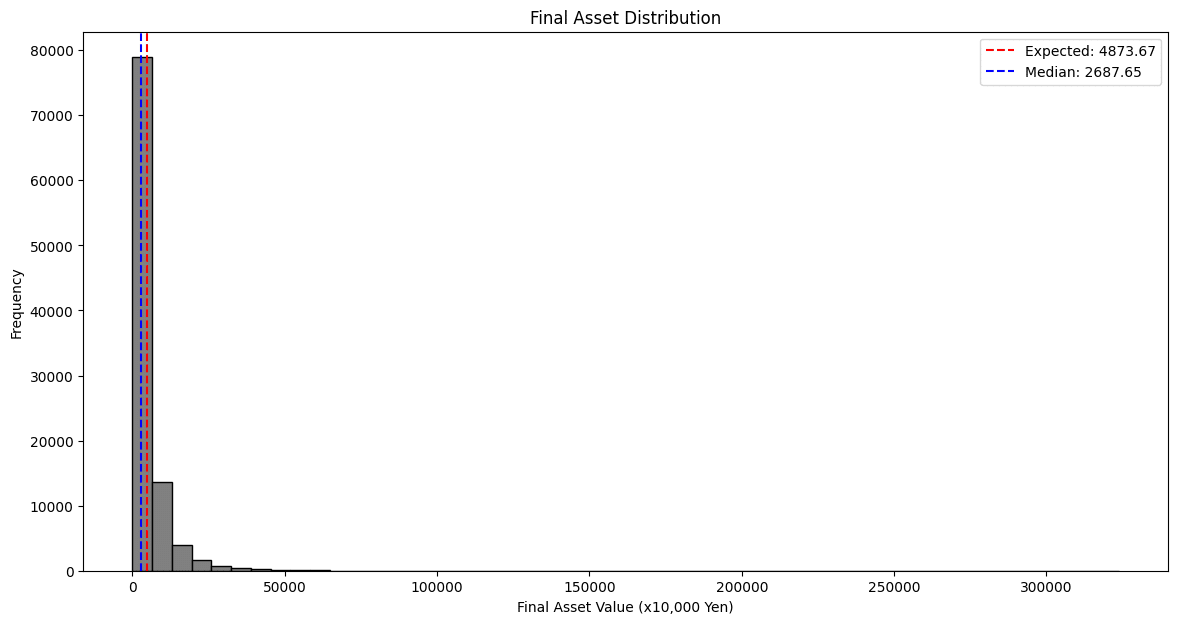
30年間のシミュレーションでは1億円に到達する可能性は11.5％に上がりました。元本割れする可能性は8.5％と下がっています。
資産分布の平均値は4874万円、中央値は2688万円となります。

シミュレーションで考える600万円をS&P500に投資しても1億円に到達する可能性はかなり低いです。特に10年後での0.014％というのは宝くじに当たるような確率でないと1億円に到達しないというようにも見えます。

元本割れする可能性は意外と高い

またもう1つ考えないといけないのはS&P500のデータからシミュレーションした場合元本割れする可能性が10年後で21.2％、20年後で13.2％、30年後で8.5％あるということです。意外と高いですよね。
1年でもシミュレーションしてみましょう。

1億円にいく可能性はゼロです（理論的にはゼロではないですがほぼゼロ）。青い折れ線はないですね。逆に元本割れする可能性は40.1%です。

投資資産の平均値:は644万円、中央値は631万円です。

普通にS&P500に600万投資しても1億円に到達するのが難しいことがわかりました。このような場合によく考えるのがよりリスクの高い個別株投資、あるいはレバレッジをかける、ということかと思います。よく”俺はリスクをとる(どや顔)”というやつです。

次回はそれぞれの手法について考えていきます。

この記事が気に入ったらサポートをしてみませんか？