
【ドップラー効果】 アニメーションによる説明(音源が動く時)
この記事で伝えたい事
アニメーションと音源が動いている場合の波の式
概要
波動はアニメーションにすると分かりやすいと思うので、pythonで描画したgifを交えて、音源が動く時のドップラー効果を解説する。
波の式
命題
正弦波$${\displaystyle y(x,t) = A \sin 2\pi\Bigr(- \frac{x}{\lambda}+ ft\Bigr)\ \ \cdots(1)}$$
の波があるとする。
また、
・音速 : $${V\ [m\cdot s^{-1}]}$$
・音源が静止している場合の波長 : $${\lambda\ [m]}$$
・音源が静止している場合の振動数 : $${f\ [s^{-1}]}$$
・音源の速度 : $${v\ [m\cdot s^{-1}]}$$
とする。この時、時刻$${t=0}$$に音源が$${x=0}$$を出発したとすると波の式は下記で与えられる。
$${ vt < x の時 \\ \ \\ \displaystyle y(x,t) = A \sin \Bigg( 2 \pi \frac{V}{V-v}\Big( - \frac{x}{\lambda }+f t \Bigl) \Biggl) = A \sin \Bigg( 2 \pi \frac{V}{(V-v)\lambda}(-x+Vt) \Biggl) \\ \ \\ x < vt の時 \\ \ \\ \displaystyle y(x,t) = A \sin \Bigg( 2 \pi \frac{V}{V+v}\Big(- \frac{x}{\lambda }+ f t \Bigl) \Biggl) = A \sin \Bigg(2 \pi \frac{V} {(V+v) \lambda }(-x+Vt) \Biggl)}$$
証明
[1] 音源の運動方向の先($${vt < x}$$)で変位を観測する場合
音源が$${vt\ [m]}$$進む間に、波は$${Vt\ [m]}$$進んでいる。よって、$${(V-v)t\ [m]}$$の幅に、$${ft}$$個の波が存在する。
このことから音源の進行方向先の波長は
$$
\lambda'=\frac{(V-v)t}{ft}=\frac{V-v}{f} = \frac{(V-v)}{V}\lambda\ [m]
$$
となる。波の伝播速度は$${V\ [m\cdot s^{-1}]}$$のままであるから、波の振動数も変更を受け
$$
f' = \frac{V}{\lambda '} = \frac{V}{V-v} f \ [s^{-1}]
$$
となる。
[2] 音源の進行方向の後ろ($${x < vt}$$)で波を観測した場合
同様に計算すると、
$$
\lambda''=\frac{(V+v)t}{ft}=\frac{V+v}{f} = \frac{V+v}{V}\lambda [m]\\ \ \\
f'' = \frac{V}{\lambda '} = \frac{V}{V+v} f \ [s^{-1}]
$$
を得る。よって、ドップラー効果によって、波の式は$${(1)}$$で与えられる。
$${Q.E.D}$$
諸条件
数値計算を行ったので、使った値を載せておく。
波の伝播速度:
$${V = \ 2.0\ [m\cdot s^{-1}]}$$
音源が止まっている時の波の振動数:
$${f = \ 0.8 \ [s^{-1}]}$$
音源が止まっている時の波の波長:
$${\displaystyle \ \lambda = \frac{v}{f} = \frac{2}{0.8}= 2.5\ [m]}$$
音源が止まっている時のアニメーション
左右に正弦波が伝播していて、左右の地点に観測者がいる状態のアニメーションがこちら。(観測者が観測する波の変位を赤点で表す)

音源が動いている時のアニメーション
音源を$${x}$$軸正の方向に一定速度で動かした時のアニメーションがこちら。
音源の速度は波の伝播速度の$${70\%}$$、すなわち$${1.4\ [m\cdot s^{-1}]}$$とした。
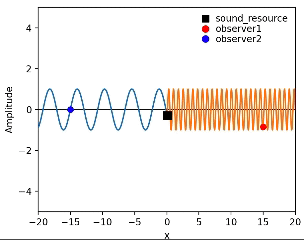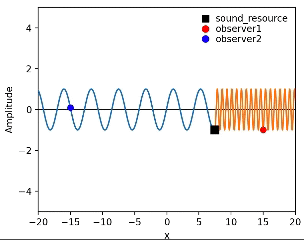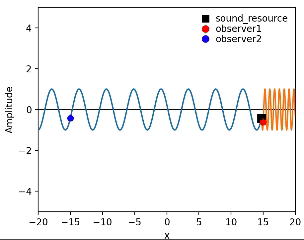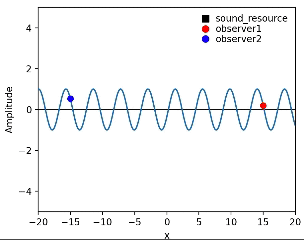
上記のアニメーションから
・音源の前方にある赤の点では波の1周期が短くなっていて
・音源の後方にある青の点では波の1周期が長くなっている
音源の速度を波の伝播速度に近づけた時
下記のアニメーションでは音源の速度を波の伝播速度の$${95\%}$$、すなわち$${1.9\ [m\cdot s^{-1}]}$$とした。

音源の速度を波の伝播速度に小さい方から近づけて行くと、ドップラー効果によって波長が$${0}$$に収束し、振動数が$${+\infty}$$に発散する。その様子が見て取れる。現象としておもしろい。
プログラム(Python)
大方はchatgptにお願いしているが、貼っておく。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
speedOfSound = 2
frequencty = 0.8
wavelength = speedOfSound / frequencty
interval_mili_time = 10
velocityOfSoundResource = 1.4
front_frequencty_of_doppler_effect = speedOfSound * frequencty / (speedOfSound - velocityOfSoundResource)
front_wavelength_of_doppler_effect = (speedOfSound - velocityOfSoundResource) * wavelength / speedOfSound
back_frequencty_of_doppler_effect = speedOfSound * frequencty / (speedOfSound + velocityOfSoundResource)
back_wavelength_of_doppler_effect = (speedOfSound + velocityOfSoundResource) * wavelength / speedOfSound
front_x = np.linspace(0, 20, 10000)
back_x = np.linspace(-20, 0, 10000)
# 波の関数
def front_wave(x, t):
return np.sin(2 * np.pi * (-(np.abs(x) / front_wavelength_of_doppler_effect) + (front_frequencty_of_doppler_effect * t)))
def back_wave(x, t):
return np.sin(2 * np.pi * ((x / back_wavelength_of_doppler_effect) + (back_frequencty_of_doppler_effect * t)))
# アニメーション更新関数
def update(frame):
t = interval_mili_time * frame / 1000 # 時間がリアルタイムになるよう調整
front_x = np.linspace(velocityOfSoundResource * t, 20, 10000)
back_x = np.linspace(-20, velocityOfSoundResource * t, 10000)
back_line.set_data(back_x, back_wave(back_x, t))
front_line.set_data(front_x, front_wave(front_x, t))
sound_resource_point.set_data([0 + velocityOfSoundResource * t], [front_wave(0 + velocityOfSoundResource * t, t)])
if velocityOfSoundResource * t < 15 :
point1.set_data([15], [front_wave(15, t)])
else:
point1.set_data([15], [back_wave(15, t)])
point2.set_data([-15], [back_wave(-15, t)])
return back_line, front_line, sound_resource_point, point1, point2
# 描画準備
fig, ax = plt.subplots(figsize=(5, 4)) # Set figure size (width, height in inches)
back_line, = ax.plot(back_x, back_wave(back_x, 0), lw=1.5)
front_line, = ax.plot(front_x, front_wave(front_x, 0), lw=1.5)
sound_resource_point, = ax.plot([0], [front_wave(0, 0)], 'ks', markersize= 8.5)
point1, = ax.plot([15], [front_wave(15, 0)], 'ro')
point2, = ax.plot([-15], [front_wave(-15, 0)], 'bo')
ax.plot([-20, 20], [0, 0], color='black', linewidth=1)
ax.set_xlim(-20, 20) # x軸の範囲
ax.set_ylim(-5, 5) # y軸の範囲
ax.set_xlabel("x")
ax.set_ylabel("Amplitude")
ax.scatter(0.65, 0.945, color='black', s=50, transform=ax.transAxes, marker='s') # 黒四角
ax.text(0.69, 0.943, "sound_resource", color='black', fontsize=10, va='center', transform=ax.transAxes)
ax.scatter(0.65, 0.895, color='red', s=50, transform=ax.transAxes) # 青丸
ax.text(0.69, 0.893, "observer1", color='black', fontsize=10, va='center', transform=ax.transAxes)
ax.scatter(0.65, 0.845, color='blue', s=50, transform=ax.transAxes) # 赤丸
ax.text(0.69, 0.843, "observer2", color='black', fontsize=10, va='center', transform=ax.transAxes)
ani = FuncAnimation(fig, update, frames=2000, interval=interval_mili_time, blit=True)
plt.show()一言
波動分野は見えない話も多いのでアニメーションで可視化すると良い気がします。
