
【気柱の共鳴】 サランラップの芯に息を吹きかけた時に聞こえる音の周波数
この記事で伝えたいこと
・長さ$${31\ [cm]}$$のサランラップ芯に息を吹きかけた時、聴こえる音の周波数の理論値と測定値は下記の表1,2,3の通り
・「Spectroid」または「Sonic Tools SVM」というスマホアプリで周波数を測定して理論値と照合出来る



概要
前回の記事ではガラス管に息を吹きかけると、聞こえてくる音の振動数についての考察を行った。今回はサランラップ芯を使う。
基本的にはガラス管の時の話と同様なのだが、両方とも自由端反射で定在波が生じるという点のみ異なる。
では、聞こえる振動数の理論値を具体的に計算してみよう。
理論
音速 : $${v =340\ [m\cdot s^{-1}]}$$とする。
サランラップの芯の長さ : $${L\ [m]}$$で表す。
波長 : $${\lambda \ [m]}$$で表す。
振動数 : $${f\ [Hz]}$$で表す。
サランラップの芯の内側で発生する、定在波(基本振動の波)の波長は、両端が開口なので(開口端補正を無視すると)
ここで$${v=f\lambda}$$を用いると、振動数は
$$
v=f_ \times \frac{2L}{n} \\ \ \\
\Leftrightarrow f = \frac{nv}{2L}\ \ \ (nは自然数)\ \cdots (1)
$$
となる。
基本振動,2倍振動,3倍振動,4倍振動の定在波の周波数$${f_1,f_2,f_3,f_4}$$は$${(1)}$$式より、それぞれ
$$
f_1 = \frac{v}{2L}\ [Hz]\\ \ \\
f_2 = \frac{v}{L}\ [Hz]\\ \ \\
f_3 = \frac{3v}{2L}\ [Hz]\\ \ \\
f_4 = \frac{4v}{2L}\ [Hz]\\ \ \\
$$
と求められる。
具体的な理論値計算(n=1,2,3,4の時)
サランラップ芯の長さを$${31\ [cm] = 0.31\ [m]}$$とする。この条件で具体的な理論値を計算してみよう。基本振動,2倍振動,3倍振動の周波数はそれぞれ、
$$
f_1 = \frac{v}{2L} = \frac{1\times 340}{2\times 0.31} \fallingdotseq 548\ [Hz] \\ \ \\
f_2 = \frac{2v}{2L} = \frac{2 \times 340}{2 \times 0.31} \fallingdotseq 1097\ [Hz]\\ \ \\
f_3 = \frac{3v}{2L} = \frac{3\times 340}{2 \times 0.31} \fallingdotseq 1645\ [Hz]
f_4 = \frac{4v}{2L} = \frac{4\times 340}{2 \times 0.31} \fallingdotseq 2194\ [Hz]
f_5 = \frac{5v}{2L} = \frac{4\times 340}{2 \times 0.62} \fallingdotseq 2742\ [Hz]
$$
となる。

サランラップの芯の内側で生じる基本振動の定在波の横波表示アニメーション
これらの周波数はヒトには「よく聞こえる音」である。
開口端補正をした具体的な理論値計算(n=1,2,3,4,5の時)
今度は開口端補正をして同様の条件で具体的な理論値を計算してみる。
$${n}$$倍振動の波長については、開口端補正を$${h}$$とすると
$$
\lambda_n = \frac{2}{n}(L+2h) \\ \ \\
$$
となる。よって、$${n}$$倍振動の周波数はそれぞれ、
$$
f_n = \frac{v}{\lambda_n} = \frac{nv}{2(L+2h)}
$$
である。
開口端補正をサランラップ芯の半径×0.6とした時
サランラップの芯の半径を$${r = 1.15[cm]}$$とすると、開口端補正は$${2 \times h= 2 \times 0.6 \times r = 2 \times 0.6\times 1.15 \times 10^{-2} = 1.38 \times 10^{-2} \ [m] = 1.38\ [cm]}$$となる。
$$
f_1 = \frac{v}{4(L+h)} = \frac{340}{2(0.31 + 0.0138)} = 525\ [Hz] \\ \ \\
f_2 = \frac{2v}{4(L+h)} = \frac{340}{2(0.31 + 0.0138)} = 1050\ [Hz] \\ \ \\
f_3 = \frac{3v}{4(L+h)} = \frac{340}{2(0.31 + 0.0138)} = 1575\ [Hz] \\ \ \\
f_4 = \frac{4v}{4(L+h)} = \frac{340}{2(0.31 + 0.0138)} = 2100\ [Hz] \\ \ \\
f_5 = \frac{5v}{4(L+h)} = \frac{340}{2(0.31 + 0.0138)} = 2625\ [Hz] \\ \ \\
$$
となった。
開口端補正をサランラップ芯の半径×0.8とした時
サランラップの芯の半径を$${r = 1.15[cm]}$$とすると、開口端補正は$${2 \times h= 2 \times 0.8 \times r = 2 \times 0.8 \times 1.15 \times 10^{-2} = 1.84 \times 10^{-2} \ [m] = 1.84\ [cm]}$$となる。
$$
f_1 = \frac{v}{4(L+h)} = \frac{340}{2(0.31 + 0.0184)} = 518\ [Hz] \\ \ \\
f_2 = \frac{2v}{4(L+h)} = \frac{340}{2(0.31 + 0.0184)} = 1035\ [Hz] \\ \ \\
f_3 = \frac{3v}{4(L+h)} = \frac{340}{2(0.31 + 0.0184)} = 1553\ [Hz] \\ \ \\
f_4 = \frac{4v}{4(L+h)} = \frac{340}{2(0.31 + 0.0184)} = 2071\ [Hz] \\ \ \\
f_5 = \frac{4v}{4(L+h)} = \frac{340}{2(0.16 + 0.0184)} = 2588\ [Hz] \\ \ \\
$$
となった。
実験による測定値
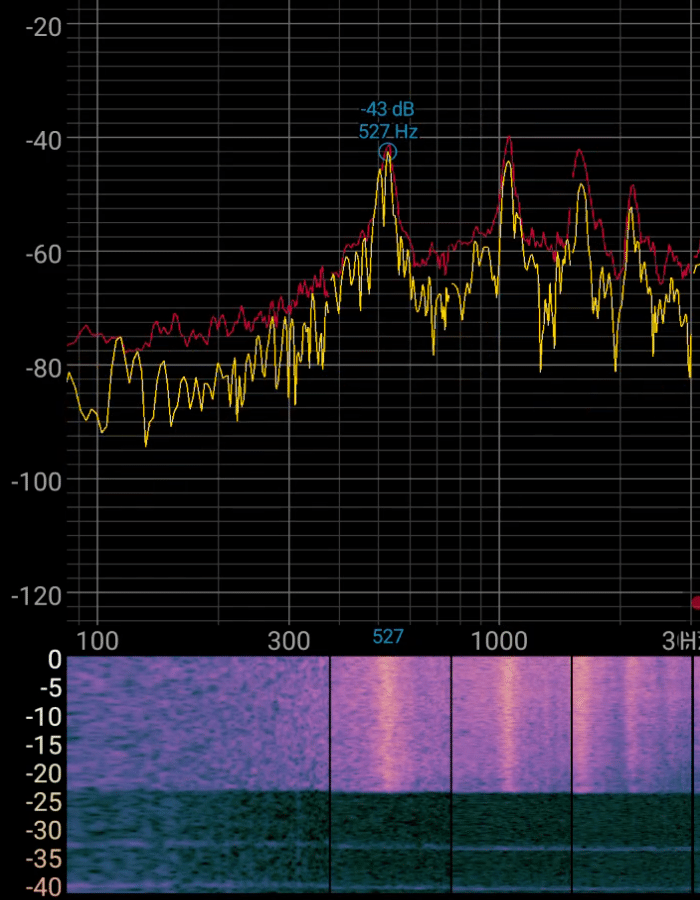
・基本振動 : $${527\ [Hz]}$$
・2倍振動 : $${1055\ [Hz]}$$
・3倍振動 : $${1594\ [Hz]}$$
が測定できた。


測定に使えるアプリ
Androidユーザー用(今回の測定はこちらで行いました)
Thanks to Carl Reinke
iPhoneユーザー用
Thanks to Takuji Matsugaki
