
【ドップラー効果】 アニメーションによる説明(観測者が動く時)
概要
波動の単元はアニメーションにすると分かりやすいと思うので、pythonで描画したgifを交えて、観測者が動く時のドップラー効果を解説する。
波の式
命題
正弦波$${\displaystyle y(x,t) = A \sin 2\pi\Bigr(- \frac{x}{\lambda} + ft\Bigr)\ \ \cdots(1)}$$
の波があるとする。今、
・音速 : $${V\ [m\cdot s^{-1}]}$$
・波長 : $${\lambda\ [m]}$$
・振動数 : $${f\ [s^{-1}]}$$ である。
観測者の速度を $${v\ [m\cdot s^{-1}]}$$とする。
観測者が時刻$${t=0}$$に$${x=0}$$を出発した場合、観測者が受ける波の式は$${\begin{aligned} \displaystyle y(vt,t) = A \sin 2\pi ft \Bigr( \frac{V-v}{V} \Bigr) \end{aligned}}$$である。
証明
(1)で$${x=vt}$$とすると
$$
y(x,t) =A \sin 2\pi\Bigr(- \frac{vt}{\lambda}+ ft\Bigr) \\ \ \\
= A\sin 2\pi\Bigr(- \frac{vt}{V}f+ ft\Bigr) \\ \ \\
=A \sin 2\pi ft\Bigr(- \frac{v}{V}+ 1 \Bigr) \\ \ \\
=A \sin 2\pi ft\Bigr( \frac{V-v}{V}\Bigr)
$$
$${Q.E.D}$$
諸条件
数値計算を行ったので、使った値を載せておく。
波の速度:$${V = \ 2.0\ [m\cdot s^{-1}]}$$
波の振動数:$${f = \ 0.8 \ [s^{-1}]}$$
波長:$${\displaystyle \ \lambda = \frac{v}{f} = \frac{2}{0.8}= 2.5\ [m]}$$
観測者が止まっている時のアニメーション
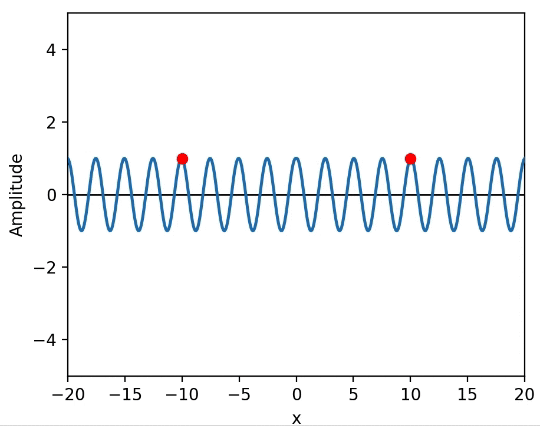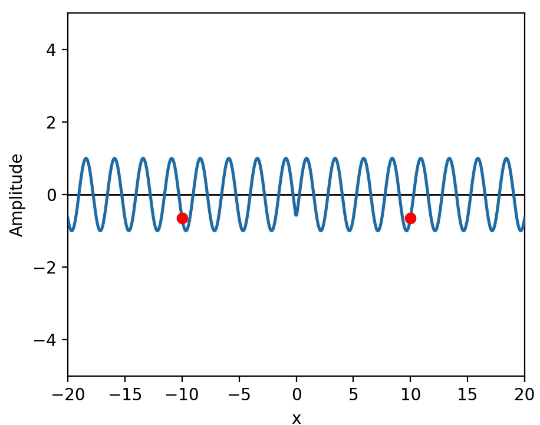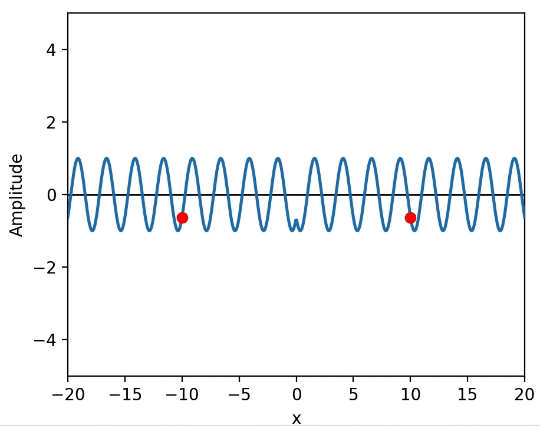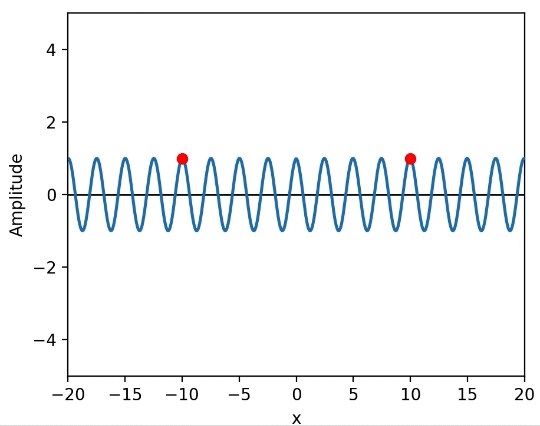
左右に正弦波が伝播していて、左右の地点に観測者がいる状態のアニメーションがこちら。(観測者が観測する波の変位を赤点で表す)
観測者が動いている時のアニメーション
左右の赤い点を$${x}$$軸正の方向に一定速度で動かした時の赤い点の動きがこちら。
観測者の速度は$${1.2\ [m\cdot s^{-1}]}$$とした。

明らかに、
・波に向かって動いている左の粒子は盛んに振動していて(1周期が短くなっていて)
・波から逃げて動いている右の粒子はゆっくりと振動している(1周期が長くなる)
ちなみに、アニメーションの後半では左の粒子は$${x}$$座標が正になって、「波から逃げる」動きになるので1周期が長くなる運動に切り替わっていることも分かる。
おまけ:特に波と同じ速度で波から逃げると
波の伝播速度と同じ速度($${2\ [m\cdot s^{-1}]}$$)で観測者が動くと、波から逃げる観測者が観測する波は変位しなくなる事もアニメーションで確認できる。

プログラム(Python)
大方はchatgptにお願いしているが、貼っておく。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
x = np.linspace(-20, 20, 500)
speedOfSound = 2
frequencty = 0.8
wavelength = speedOfSound / frequencty
interval_mili_time = 20
velocityOfObserver = 1.2 # 観測者の動きを止める場合は0に。波と同じ速度なら2に。
# 波の関数
def wave(x, t):
return np.sin(2 * np.pi * ( - (np.abs(x) / wavelength) + (frequencty * t)))
# アニメーション更新関数
def update(frame):
t = interval_mili_time * frame / 1000 # 時間がリアルタイムになるよう調整
line.set_ydata(wave(x, t)) # yデータを更新
point1.set_data([10 + velocityOfObserver * t], [wave(10 + velocityOfObserver * t, t)])
point2.set_data([-10 + velocityOfObserver * t], [wave(-10 + velocityOfObserver * t, t)])
return line, point1, point2
# 描画準備
fig, ax = plt.subplots(figsize=(5, 4)) # Set figure size (width, height in inches)
line, = ax.plot(x, wave(x, 0), lw=1.8)
point1, = ax.plot([10], [wave(10, 0)], 'ro')
point2, = ax.plot([-10], [wave(-10, 0)], 'ro')
# y=0の水平線を描画
ax.plot([-20, 20], [0, 0], color='black', linewidth=1)
ax.set_xlim(-20, 20) # x軸の範囲
ax.set_ylim(-5, 5) # y軸の範囲
ax.set_xlabel("x")
ax.set_ylabel("Amplitude")
ani = FuncAnimation(fig, update, frames=1000, interval=interval_mili_time, blit=True)
plt.show()一言
アニメーションにするとやっぱり大分分かりやすい気がしました。
