最適なポートフォリオを構築する

サブテーマ：自己流最適ポートフォリオの作り方

１　初めに

　今回は、投資中級者向け投稿になります。前回まで金や債券の最適な割合についての記事でした。しかしETFには多種多様であり、何をどう組み合わせたら良いのかわからないと思います。
そこで今回は、PYTHONで簡単に最適組み合わせできるコードを使って、SBI証券で買付手数料が無料となるSBI ETFセレクションから、株や債券、金、不動産など選りすぐり最適な組み合わせを算出してみます。これを名付けて自己流最適ポートフォリオの作り方として紹介します。

今回の結論：
　①過去実績ベースでの最適化ポートフォリオは、
　　　S＆P500やQQQより　VGT：GLD＝６：４　
　②資産形成期：　効率化フロンティア曲線上の最大リターンがベスト
　　取崩期　　：　最適化ポートフォリオが良い傾向

左）最適化ポートフォリオのリスク&リターン　右）最適化ポートフォリオの配分％

最適化ポートフォリオの取崩シミュレーション（元本5000万を年360万　年率7.2％時）

---

SBI ETFセレクション｜SBI証券

---

知人よりプログラム部分が難しくてよくわからないとご指摘をいただきました。そのためこのチャンネルでは、PYTHONを使った米国株投資に関わるさまざまな調査の結果OUTPUTにこだわった記事にします。投資に関わる身近な疑問にも答えていきますので、投資リテラシー向上にお役立ちを目指します！！
　なお、全ての解析データは引き続き、PYTHONを活用してコード全文も掲載します。Googleコラボならまずは”コピペ”でチャレンジできます。これから勉強始めたい方にも、プログラミングで何ができるのかを知る良いチャンスとなればと思っていますので応援お願いします！！

---

２　豆知識

１）シャープレシオを最大化するとは？

　シャープレシオを最大化することは、投資ポートフォリオを最適化する戦略の一つです。シャープレシオは、投資のリターンをリスク（標準偏差）で割った値であり、投資による超過リターン（リスクフリーレート以上のリターン）をリスクで割って算出します。シャープレシオが高いポートフォリオは、単位リスク当たりのリターンが高く、投資の効率が良いと評価されます。したがって、シャープレシオを最大化する戦略は、同じリターンを目指す場合に最小のリスクで達成するか、同じリスクレベルで最大のリターンを得るポートフォリオを選択することを目的としています。

２）効率的フロンティアとは？

　効率的フロンティアは、与えられたリスクレベルで最大リターンを提供するポートフォリオの組み合わせを表すグラフ上の曲線です。この概念はポートフォリオ理論の中核をなすもので、特定のリスクに対して最も効率的な（最大の期待リターンを持つ）投資ポートフォリオを識別するために使用されます。効率的フロンティアは、異なるリスクレベルにおける最適なポートフォリオのセットを視覚的に示し、投資家が自身のリスク許容度に応じた適切な投資選択を行うための指標を提供します。効率的フロンティア上のどのポイントも「効率的」と見なされ、そのポイント以下のリターンは他のどの組み合わせでも達成できない最大値となります。今回の調査では、効率的フロンティア曲線上かつシャープレシオが最大になるところを、最適ポートフォリオとして、その時のリターンとリスク、アセットの組み合わせ割合を算出しています。

３　実践

１）調査内容

　今回、SBI ETFセレクション10種を2015年10月から取得し、効率化フロンティアをプロットし、その中でシャープレシオ最大化した時の投資割合、参考まで、S&P500（VOO）との相関を一度にプロットしています。
　その後検証のため、取崩時と、積立時の最適ポートフォリオと、S &P500（VOO）,オルカン（VT）、情報技術セクター（VGT)との比較を毎度のモンテカルロシミュレーションで確認しました。

SBI ETFセレクション
　VT：バンガードトータルワールドストック（オルカン相当）
　VTI：バンガードトータルストックマーケット（全米株）
　VOO：バンガードS&P500
　QQQ：インベスコQQQトラストシリーズ１（NASDAQ100）
　SPYD ：SPDRポートフォリオS&P500高配当
　VGT：バンガード米国情報技術セクター
　EPI：ウィズダムツリーインド株収益ファンド
　AGG：iシェアーズコア米国総合債券市場
　GLDM：SPDRゴールドミニシェアーズトラスト＊＊
　IYR：iシェアーズ米国不動産
　　　＊＊GLDMは設定後の期間が短いため、調査はGLDを使用

２）データ取得と時系列グラフのプロット

Yahoo Financeから2015年10月からの株価データを取得し、時系列にプロットします。比較のため2015年10月を100としたグラフと、対軸にしたグラフをプロットします。

pip install japanize-matplotlib

import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import japanize_matplotlib  # 日本語表示に対応

# 対象のティッカーシンボル
tickers = ['VT', 'VTI', 'VOO', 'QQQ', 'SPYD', 'VGT', 'EPI', 'AGG', 'GLD', 'IYR']

# データの取得
data = yf.download(tickers, start="2015-11-01", end=pd.Timestamp.now().strftime('%Y-%m-%d'))['Adj Close']

# ティッカーの順序を正確に指定
data = data[['VT', 'VTI', 'VOO', 'QQQ', 'SPYD', 'VGT', 'EPI', 'AGG', 'GLD', 'IYR']]

# 月別にリサンプリングして、月の初めのデータを取得
monthly_data = data.resample('MS').first()

#１　時系列の線グラフを描画
plt.figure(figsize=(12, 5))  # グラフのサイズを設定
# 各ティッカーについて線グラフをプロット
for ticker in tickers:
    plt.plot(monthly_data[ticker], label=ticker)
# グラフのタイトルと軸ラベルを設定
plt.title('月次調整後終値の時間推移')
plt.xlabel('日付')
plt.ylabel('調整後終値')
plt.legend()  # 凡例を表示

# 基準日の価格で各ティッカーの価格を割り、100をかけてインデックス化
normalized_data = monthly_data.apply(lambda x: x / x.iloc[0] * 100)

#２　インデックス化されたデータの時系列グラフを描画
plt.figure(figsize=(12, 5))  # グラフのサイズを設定
# 各ティッカーについて線グラフをプロット
for ticker in tickers:
    plt.plot(normalized_data[ticker], label=ticker)
# 初期線（100）を追加
plt.axhline(y=100, color='red', linestyle='--', linewidth=1)
# グラフのタイトルと軸ラベルを設定
plt.title('正規化された月次調整後終値の時間推移')
plt.xlabel('日付')
plt.ylabel('正規化価格 (基準=100 on 2015-11-01)')
plt.legend()

#３　対数軸のグラフの描写
plt.figure(figsize=(12, 5))
# 各ティッカーについて線グラフをプロット
for ticker in tickers:
    plt.plot(normalized_data[ticker], label=ticker)
# 初期線（100）を追加
plt.axhline(y=100, color='red', linestyle='--', linewidth=1)
# グラフのタイトルと軸ラベルを設定
plt.title('対数スケールにおける正規化された月次調整後終値の時間推移')
plt.xlabel('日付')
plt.ylabel('対数正規化価格 (基準=100 on 2015-11-01)')
plt.legend()
# y軸を対数スケールに設定
plt.yscale('log')

# グラフを表示
plt.show()

時系列プロット

2015年10月を100にしてプロット（上通常軸、下対数軸）

３）効率化フロンティア&シャープレシオ最大化のプロット

いよいよ本番ですが、コードとしては下記だけですので、コピペで簡単に実行できます。リターン・リスク（標準偏差）の計算、シャープレシオの計算、効率化フロンティアの曲線の作図ができます。
なお、追加でS&P500との相関係数を確認できるようなコードとしています。
＊相関係数とはどれぐらい連動しているかを示す指標です。アセットの組み合わせを考える際には非常に参考にするべき指標のため、アレンジしてみました。
＊PyPortfolioOpt　効率化フロンティア計算のためのライブラリ
＊ffn 最大ドローダウン計算のため使用したライブラリ

!pip install PyPortfolioOpt
!pip install ffn

from pypfopt import expected_returns, risk_models, EfficientFrontier, plotting

# 日次リターンの計算
daily_returns = data.pct_change()

# SPYに対する相関係数を計算
correlations = daily_returns.corr().loc['VOO']

# 月次リターンの計算
monthly_data = data.resample('M').last()
monthly_returns = monthly_data.pct_change().dropna()

# 年化された期待リターンとリスク（共分散行列）の計算
mean_returns = expected_returns.mean_historical_return(monthly_data, frequency=12)
cov_matrix = risk_models.sample_cov(monthly_data, frequency=12)

# 各ティッカーのリスク（標準偏差）とリターンの計算
individual_risks = np.sqrt(np.diag(cov_matrix))
individual_returns = mean_returns.values

# 最適化：シャープレシオを最大化
ef = EfficientFrontier(mean_returns, cov_matrix)
weights = ef.max_sharpe()
cleaned_weights = ef.clean_weights()

# 最適化されたポートフォリオのパフォーマンス計算
expected_return, volatility, sharpe_ratio = ef.portfolio_performance(verbose=True)

# 効率的フロンティアの点を生成
ef_new = EfficientFrontier(mean_returns, cov_matrix)
fig, ax = plt.subplots(1, 3, figsize=(18, 6))

# 散布図と効率的フロンティア
ax[0].scatter(volatility, expected_return, color='red', s=100, label='最適化されたポートフォリオ')
ax[0].scatter(individual_risks, individual_returns, color='blue', s=50)  # 各ティッカー
for i, txt in enumerate(mean_returns.index):
    ax[0].annotate(txt, (individual_risks[i], individual_returns[i]))
plotting.plot_efficient_frontier(ef_new, ax=ax[0], show_assets=True)

ax[0].set_title('ポートフォリオおよび各ティッカーのリスクとリターン')
ax[0].set_xlabel('標準偏差（リスク）')
ax[0].set_ylabel('期待リターン')
ax[0].grid(True)
ax[0].legend()

# ウェイトの棒グラフ
ax[1].bar(cleaned_weights.keys(), cleaned_weights.values(), color='green')
ax[1].set_title('ポートフォリオの最適化されたウェイト')
ax[1].set_xlabel('資産')
ax[1].set_ylabel('ウェイト')
ax[1].grid(True)

# SPYとの相関係数の棒グラフ
correlation_values = correlations.drop('VOO')  # VOO自体の相関は除外
ax[2].bar(correlation_values.index, correlation_values.values, color='purple')
ax[2].set_title('SPYとの相関係数')
ax[2].set_xlabel('資産')
ax[2].set_ylabel('相関係数')
ax[2].grid(True)

plt.tight_layout()
plt.show()

左）効率化フロンティア&シャープレシオ最大化　中）最適化時の保有割合　右）相関係数vsVOO

効率化フロンティアの分布は青線で示され、この線上がリスクとリターンのバランスに優れた投資効率の良い線です。この線上でシャープレシオが最大となる点が赤丸です。この時のリスクとリターン、シャープレシオは小さいですが、左上に出力されています。
　最適化後：リターン15.9％、リスク13.6％、シャープレシオ1.02%
この時の保有割合が中央のグラフです。結局VGTが６割、金４割が最適な結果となりました。
　結果：過去実績ベースでの最適化ポートフォリオは、
　　　S＆P500やQQQより　VGT：GLD＝６：４　
　　　　（厳密には、VGT：GLD：インド＝5.7:4.2:0.1)
　相関係数は、AGG、GLDは低いことがわかりますが、AGGは先ほどの時系列プロットの通り、株価大暴落の際には同様に下落しますので、組み合わせとしてはそれほど最適ではない結果です。
＊国債だけのEFTであれば株式と相関が低く、組み合わせに最適です。しかしAGGには社債が含まれ、この社債分が株価暴落時には株価と同様に下落する傾向があります。

３）シミュレーションで確認

　最適なポートフォリオは計算できましたが、具体的にどの程度の効果が見込めるのかわからないと思います。その効果見込みを、計算したリスクとリターンを使ってモンテカルロシミュレーションを実行してみます。
　まず、長期のシミュレーションで信頼性を高めるため、年率リターン、年次換算標準偏差を計算します。また、あらためてETF単独のシャープレシオ、最大ドローダウンも計算し、テーブルに出力します。

import ffn  # このライブラリを使用して最大ドローダウンを計算


# 年次リターン、標準偏差、シャープレシオ、最大ドローダウンを計算
results = []

for ticker in tickers:
    # ティッカーごとの月次クローズ価格
    prices = monthly_data[ticker].dropna()
    
    # 月次リターンの計算
    monthly_returns = ffn.to_returns(prices).dropna()
    
    # 年次リターンの計算（月次リターンの平均 * 12）
    annual_return = monthly_returns.mean() * 12
    
    # 年次標準偏差の計算（月次ボラティリティ * sqrt(12)）
    annual_vol = monthly_returns.std() * np.sqrt(12)
    
    # シャープレシオ
    sharpe_ratio = annual_return / annual_vol
    
    # 最大ドローダウン
    max_drawdown = ffn.calc_max_drawdown(prices)
    
    results.append({
        "Ticker": ticker,
        "Annual Return": annual_return,
        "Annual Volatility": annual_vol,
        "Sharpe Ratio": sharpe_ratio,
        "Max Drawdown": max_drawdown
    })

# 結果をDataFrameに変換
results_df = pd.DataFrame(results)
results_df.set_index('Ticker', inplace=True)

# 結果の表示
results_df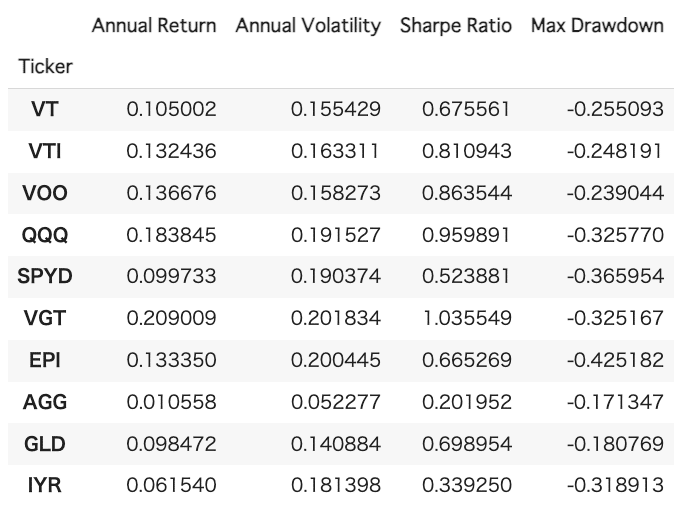

①老後・FIRE期　取崩シミュレーション
　得られた年率リターン、リスクを最適ポートフォリオ（ティッカー名：BEST）とし、比較として、VOO（S &P500）、VT（全世界株式）、VGT（情報技術セクター）単独のティッカーでシミュレーションします。
今回5000万円の元手に対し、年360万円：年率7.2％の定額取り崩しの際の資産額の推移を時系列で表示します。
＊今回は手動で年次リターンと年次標準偏差（リスク）を入力してシミュレーションするコードとしてます。それぞれリスクとリターンを変更

# 必要なライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# パラメータ設定
initial_investment = 5000  # 初期投資額（5000万円）
withdrawal_amount = 360  # 年次取り崩し額（360万円）
investment_duration = 10  # 投資期間（年）
simulations = 100  # シミュレーション回数

# tickersリストを定義
tickers = ['BEST', 'VOO', 'VT', 'VGT']

# 年次リターンと年次標準偏差（手動設定）
annual_returns = {'BEST': 0.159, 'VOO': 0.137, 'VT': 0.105, 'VGT': 0.209}
annual_std_devs = {'BEST': 0.136, 'VOO': 0.158, 'VT': 0.155, 'VGT': 0.200}

# 各シミュレーションの資産額を保存する配列の初期化
all_time_series = []

for ticker in tickers:
    annual_return_mean = annual_returns[ticker]
    annual_return_std = annual_std_devs[ticker]
    # この配列に各シミュレーションの時系列データを保存
    time_series_simulations = np.zeros((simulations, investment_duration))

    for simulation in range(simulations):
        total_value = initial_investment
        for year in range(investment_duration):
            annual_return = np.random.normal(annual_return_mean, annual_return_std)
            total_value = total_value * (1 + annual_return) - withdrawal_amount
            # 各年の資産額を保存
            time_series_simulations[simulation, year] = max(total_value, 0)

    all_time_series.append(time_series_simulations)

fig, axes = plt.subplots(nrows=4, ncols=1, figsize=(10, 12))
axes = axes.flatten()

# y軸の上限を設定
y_max = initial_investment * 3

for i, ticker in enumerate(tickers):
    ax = axes[i]
    time_series_simulations = all_time_series[i]

    # 中央値、上5％、下5％の計算
    median_values = np.median(time_series_simulations, axis=0)
    percentile_95 = np.percentile(time_series_simulations, 95, axis=0)
    percentile_5 = np.percentile(time_series_simulations, 5, axis=0)

    # 各シミュレーションの時系列データをプロット
    for simulation in range(simulations):
        ax.plot(range(investment_duration), time_series_simulations[simulation], alpha=0.2, color='blue')

    # 中央値、上5％、下5％のプロット
    ax.plot(range(investment_duration), median_values, color='green', label='中央値', linewidth=2)
    ax.plot(range(investment_duration), percentile_95, color='orange', label='上5％', linestyle='--')
    ax.plot(range(investment_duration), percentile_5, color='purple', label='下5％', linestyle='--')

    # 元本の線を黒の点線で追加
    ax.axhline(y=initial_investment, color='black', linestyle=':', label='元本')

    ax.set_title(f'{ticker} - 取崩時：資産額の時系列推移')
    ax.set_xlabel('年')
    ax.set_ylabel('資産額')
    ax.legend()
    ax.grid(True)

    # すべてのサブプロットのy軸の範囲を設定
    ax.set_ylim([0, y_max])

plt.tight_layout()
plt.show()

元本5000万円から年360万円定額取崩シミュレーションの結果

取崩シミュレーションの結果、最適ポートフォリオ（BEST）は、他の単独VOO（S &P500）、VT（全世界株式）、VGT（情報技術セクター）に比べ、元本割れの確率が低いことがわかります。また最もリターンが高いVGTは、ばらつきが大きいですが、比較的変動幅が狭く安定した元本推移となっています。

②資産形成期のシミュレーション
同様に資産形成期をシミュレーションします。リターンとリスクの設定値は取崩シミュレーションと同じ値としています。

# 必要なライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# パラメータ設定
initial_investment = 300  # 初期投資額（200万円）
monthly_investment = 3  # 月次積立額（3万円）
investment_duration = 360  # 投資期間（月）
simulations = 100  # シミュレーション回数

# tickersリストを定義
tickers = ['BEST', 'VOO', 'VT', 'VGT']

# 年次リターンと年次標準偏差を月次リターンへ変換
monthly_returns = {ticker: (1 + annual_returns[ticker])**(1/12) - 1 for ticker in tickers}
monthly_std_devs = {ticker: annual_std_devs[ticker] / np.sqrt(12) for ticker in tickers}

# 各シミュレーションの資産額を保存する配列の初期化
all_time_series = []

for ticker in tickers:
    monthly_return_mean = monthly_returns[ticker]
    monthly_return_std = monthly_std_devs[ticker]
    # この配列に各シミュレーションの時系列データを保存
    time_series_simulations = np.zeros((simulations, investment_duration))

    for simulation in range(simulations):
        total_value = initial_investment
        for month in range(investment_duration):
            monthly_return = np.random.normal(monthly_return_mean, monthly_return_std)
            total_value = total_value * (1 + monthly_return) + monthly_investment
            # 各月の資産額を保存
            time_series_simulations[simulation, month] = total_value

    all_time_series.append(time_series_simulations)

fig, axes = plt.subplots(nrows=len(tickers), ncols=1, figsize=(10, 4 * len(tickers)))
axes = axes.flatten() if len(tickers) > 1 else [axes]

# y軸の上限を設定
y_max = (initial_investment + monthly_investment * investment_duration) * 5

for i, ticker in enumerate(tickers):
    ax = axes[i]
    time_series_simulations = all_time_series[i]

    # 中央値、下5％、上95％の計算
    median_values = np.median(time_series_simulations, axis=0)
    percentile_5 = np.percentile(time_series_simulations, 5, axis=0)
    percentile_95 = np.percentile(time_series_simulations, 95, axis=0)

    # 各シミュレーションの時系列データをプロット
    for simulation in range(simulations):
        ax.plot(range(investment_duration), time_series_simulations[simulation], alpha=0.2, color='blue')

    # 中央値、下5％、上95％のプロット
    ax.plot(range(investment_duration), median_values, color='green', label='中央値', linewidth=2)
    ax.plot(range(investment_duration), percentile_5, color='orange', linestyle='--', label='下5％')
    ax.plot(range(investment_duration), percentile_95, color='purple', linestyle='--', label='上95％')

    # 元本の推移をプロット（黒の点線）
    total_principal_over_time = initial_investment + np.arange(investment_duration) * monthly_investment
    ax.plot(total_principal_over_time, color='black', linestyle=':', label='元本の推移')

    ax.set_title(f'{ticker} - 一括＆積立時：資産額の時系列推移')
    ax.set_xlabel('月')
    ax.set_ylabel('資産額')
    ax.legend()
    ax.grid(True)

    # すべてのサブプロットのy軸の範囲を設定
    ax.set_ylim([0, y_max])

plt.tight_layout()
plt.show()

資産形成期のシミュレーション結果では、VGT（情報技術セクター）が良い傾向に見えます。資産形成期においては、効率化フロンティア曲線上右上に位置するVGTが良い結果になり得る結果が示されています。

結論：資産形成期　効率化フロンティア曲線　右上がベスト
　　　取崩期　　　効率化フロンティア曲線上かつシャープレシオ最大
　　　　　　　　　（＝今回の最適化ポートフォリオ）　が良さそう

４　まとめ

　今回、自分で作る自己流最適ポートフォリオの作り方ということでPYTHONでお手軽に最適なアセット割合を計算できるコードを紹介しました。
今回の最適ポートフォリオが今後もベストである保証はありませんが、VGTでなくてもNASDAQ100やS&P500などの株式を6割、４割をGOLDを保有することは過去データからは有効な結果を示しています。
　皆様の投資生活の参考になれば幸いです。

＊今回の結果も、過去１０年の実績をもとにシミュレーションした結果です。今後の結果を保証するものではありません。実際の投資判断はご自身にてお願いいたします。

---

以下、過去記事、AI時系列予測等のご紹介
他サイトですがココならで、A I（LSTM）を使った株価予測の販売もやってます。こちらではFREDから、失業率や２年１０年金利、銅価格等結果も取得しLSTMモデルで予測するコードとなってますので興味があれば見てみてください。またその他２件も米国株投資とは直接関係はありませんがプログラム入門におすすめですのでみてみてください。

APPLE（変更可）米株価予測コード販売します AI・LSTMモデルで5日後を予測するpythonコード | 株式・各種投資の相談 | ココナラ

機械学習・重回帰分析　おすすめプログラム販売します 散布図（回帰式、相関係数、P値）・重回帰分析（特徴量評価） | 機械学習 | ココナラ

機械学習LightGBM コード販売します Deep Learning, 特徴量解析，SHAP値 | 機械学習 | ココナラ

---

チャンネル紹介：Kota＠Python＆米国株投資チャンネル

Kota＠Python＆米国株投資チャンネル｜note

過去の掲載記事：興味があればぜひ読んでください。
グラフ化集計の基礎：S &P500と金や米国債を比較してます。

移動平均を使った時系列予測

---