FIRE　取崩失敗確率（定率編）

サブテーマ：定率取崩できる金額をシミュレーション

１　初めに

　前回１０～５０万円/月の定額取り崩ししたときの元本確保＝FIRE成功をシミュレーションしてみました。今回は毎月年率換算で４％～１２％をそれぞれの月にわけて取り崩した場合の元本割れ（失敗確率）を可視化してみます。
PYTHONであればいろいろな条件がシミュレーションできますので、ぜひみてみてください。

今回のまとめ：
資産7000万円を月々４％～１２％（年率換算）取り崩した10年後の資産額
　対象：S＆P500,NASDAQ100,オルカン（相当）,オリジナルPF

S＆P500の場合
　　→ほとんどの人は年率４～５％取り崩しても余裕で生きていける
　　中央値は６０万円/月が可能
　　ただし、４％取り崩しでも５人に１人の確率で失敗（資産が減る）

各月定率取り崩し後の資産額(S&P500)

各月定率取り崩し時、中央の人の取り崩し額(S&P500)

各月定率取り崩し時、下位５％の人の取り崩し額(S&P500)

---

知人よりプログラム部分が難しくてよくわからないとご指摘をいただきました。そのためこのチャンネルでは、PYTHONを使った米国株投資に関わるさまざまな調査の結果OUTPUTにこだわった記事にします。投資に関わる身近な疑問にも答えていきますので、投資リテラシー向上にお役立ちを目指します！！
　なお、全ての解析データは引き続き、PYTHONを活用してコード全文も掲載します。Googleコラボで動作確認したコードですので、まずは”コピペ”でチャレンジできます。これから勉強始めたい方にも、プログラミングで何ができるのかを知る良いチャンスとなればと思っていますので応援お願いします！！

---

２　豆知識

１）定率取り崩しと4%ルールとは（おさらい）

　定率取り崩しは、資産を一定の割合で取り崩す方法です。4%ルールはその具体的な例で、退職後の生活費として毎年資産の4%を引き出す戦略です。このルールは、トリニティ大学の研究に基づき、30年間資産が枯渇しない確率が高いとされています。注意すべきはインフレ調整後の4%を基準とする必要がありますので、今後もインフレが進む場合にはこの額以上の取り崩しが必要となりますのでご注意ください。

３　実践

１）実施内容

　今回以前の記事の通りです。
YahooFinaceから過去20年分の株価実績値を取得し、年率リターンと年率リスク（標準偏差）を算出しその値を使います。
　対象はS＆P500としてSPY、NASDAQ100としてQQQ、全世界株（オルカン相当）としてVT、比較として米国債券TLT,IEF・金GLDを取得しています。なおこの期間のベストポートフォリオ（以下PF）算出コードは以前の記事を参照ください）QQQ６０％、TLT１０％、金３０％のオリジナルポートフォリオの４つを選択しています。
　対象：SPY　S＆P500
　　　　QQQ　NASDAQ100（ハイテク大型）
　　　　VT　　オルカン相当
　　　　PORT　過去ベストポートフォリオ（PF）
今回のシミュレーションでの初期額も７０００万円としています。これは１億円ためてFIREしようとしても、実際リスク資産（株や債券）に回すお金はこのぐらいで、残り3000万円は現金としてや、今すぐ使えないお金だったりする可能性を考慮しています。
その初期元本を月々年率換算で４％～１２％取り崩した場合の投資残額の１０年後を各５００回シミュレーションし残りの資産額をグラフで出力します。

２）実践　

実際にモンテカルロシミュレーションしますが、コード自体は今までと変わりません。（初期投資額や運用期間、投資商品を変えた場合等は、それぞれのパラメーターをいじって実行すると簡単に実行できますので、ぜひトライしてみてください。）

# 必要なライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib

# パラメータ設定
initial_investment = 7000  # 初期投資額（万円）
monthly_investment = 0  # 月次積立額（万円）
investment_duration = 120  # 投資期間（月）
withdrawal_start_month = 0  # 取崩開始月（月数）
simulations = 500  # シミュレーション回数
annual_withdrawal_rates = np.arange(0.04, 0.13, 0.01)  # 年率4％〜12％を1％刻みで取り崩す

# tickersリストを定義
tickers = ['SPY', 'QQQ', 'VT', 'Port']

# 年次リターンと年次標準偏差（手動設定）
annual_returns = {'SPY': 0.127, 'QQQ': 0.172, 'VT': 0.100, 'Port': 0.131}
annual_std_devs = {'SPY': 0.179, 'QQQ': 0.211, 'VT': 0.179, 'Port': 0.157}

# 年次リターンと年次標準偏差を月次リターンへ変換
monthly_returns = {ticker: (1 + annual_returns[ticker])**(1/12) - 1 for ticker in tickers}
monthly_std_devs = {ticker: annual_std_devs[ticker] / np.sqrt(12) for ticker in tickers}

# 各取り崩し率に対する結果を保存する辞書
results = {ticker: {'median': [], 'percentile_5': [], 'percentile_10': [], 'percentile_20': []} for ticker in tickers}

for ticker in tickers:
    monthly_return_mean = monthly_returns[ticker]
    monthly_return_std = monthly_std_devs[ticker]

    for annual_withdrawal_rate in annual_withdrawal_rates:
        monthly_withdrawal_rate = (1 + annual_withdrawal_rate)**(1/12) - 1
        # この配列に各シミュレーションの最終資産額を保存
        final_values = np.zeros(simulations)

        for simulation in range(simulations):
            total_value = initial_investment
            for month in range(investment_duration):
                monthly_return = np.random.normal(monthly_return_mean, monthly_return_std)
                if month < withdrawal_start_month:
                    # 資産形成期
                    total_value = total_value * (1 + monthly_return) + monthly_investment
                else:
                    # 取崩し期
                    total_value = total_value * (1 + monthly_return) - total_value * monthly_withdrawal_rate
                if total_value <= 0:
                    total_value = 0
                    break
            final_values[simulation] = total_value

        # 中央値、下5％、下10％、下20％の最終資産額を計算して保存
        results[ticker]['median'].append(np.median(final_values))
        results[ticker]['percentile_5'].append(np.percentile(final_values, 5))
        results[ticker]['percentile_10'].append(np.percentile(final_values, 10))
        results[ticker]['percentile_20'].append(np.percentile(final_values, 20))

# 結果をプロット
fig, axes = plt.subplots(nrows=len(tickers), ncols=1, figsize=(10, 4 * len(tickers)))
axes = axes.flatten() if len(tickers) > 1 else [axes]

# 統一されたY軸レンジ
y_min, y_max = 0, 20000  # 適切なレンジを設定

for i, ticker in enumerate(tickers):
    ax = axes[i]

    ax.plot(annual_withdrawal_rates * 100, results[ticker]['median'], label='中央値', color='green')
    ax.plot(annual_withdrawal_rates * 100, results[ticker]['percentile_5'], label='下5％', color='orange', linestyle='--')
    ax.plot(annual_withdrawal_rates * 100, results[ticker]['percentile_10'], label='下10％', color='purple', linestyle='--')
    ax.plot(annual_withdrawal_rates * 100, results[ticker]['percentile_20'], label='下20％', color='blue', linestyle='--')

    # 初期投資額のラインを追加
    ax.axhline(y=initial_investment, color='black', linestyle=':', label='初期投資額')

    ax.set_title(f'{ticker} - 年率取り崩しに対する最終資産額の変化')
    ax.set_xlabel('年率取り崩し額（％）')
    ax.set_ylabel('最終資産額（万円）')
    ax.legend()
    ax.grid(True)

    # Y軸のレンジを統一
    ax.set_ylim([y_min, y_max])

plt.tight_layout()
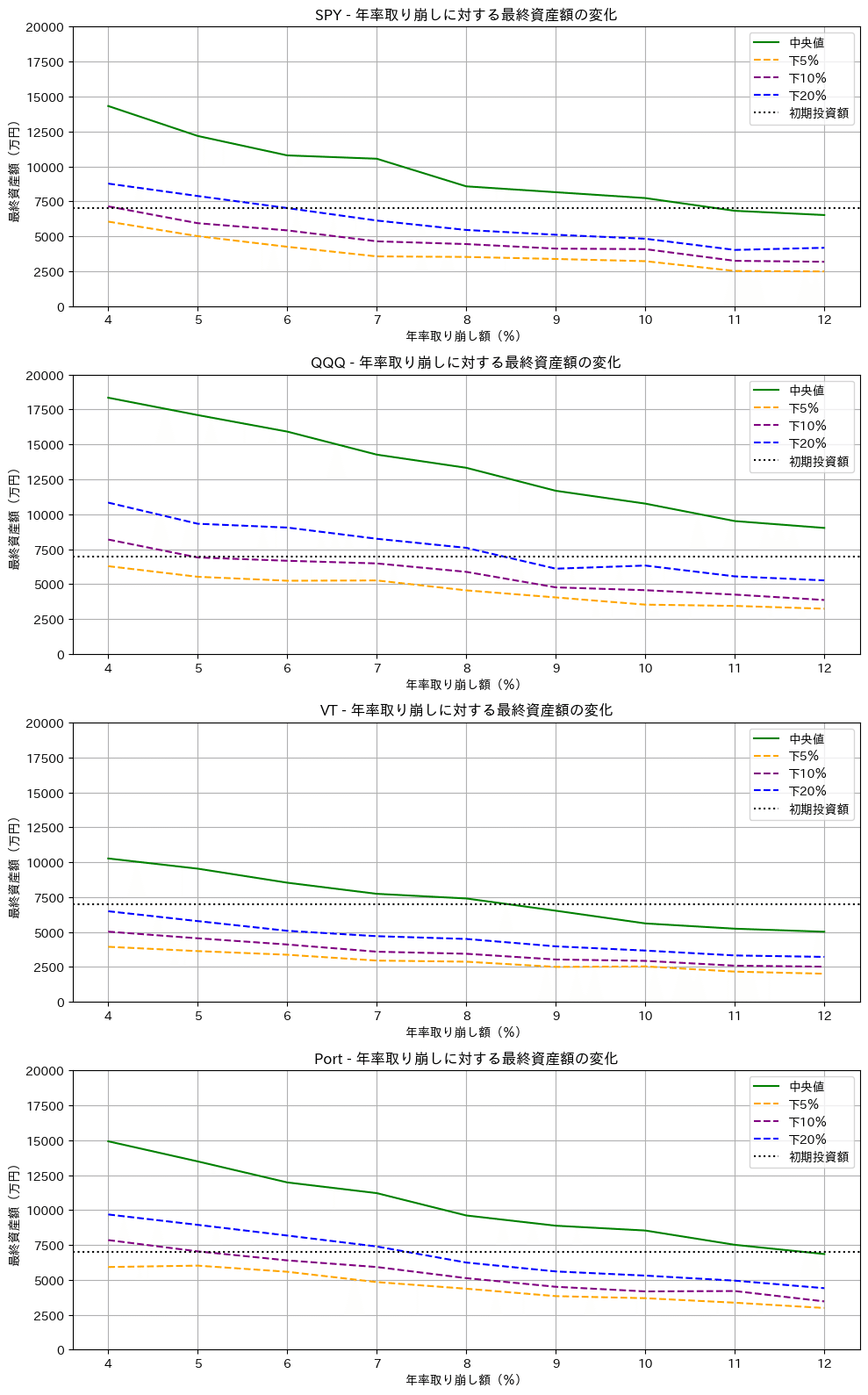
plt.show()

実行した結果が下記です。S＆P500では中央値でいえば年率１０％でも元本が確保できています。よく言われる４％ルールでいえば、下位１０％（１０人に１人以下）の確率で失敗する額となります。（注意元本が枯渇する確率ではないのでご注意を）
　この確率は、QQQや、リスク・リターンを改善したPFでは改善していますが、S＆P５００よりリターンの劣るVTではその確率が高くなっていることがわかります。これは過去実績が今後１０年続く場合の確率ではありますが、今後１０年は過去２０年に比べてS＆P５００のリターンが劣ると同じようになる可能性がありますので、その視点でみてもらえればと思います。

定率取り崩しした場合の１０年後の最終資産額

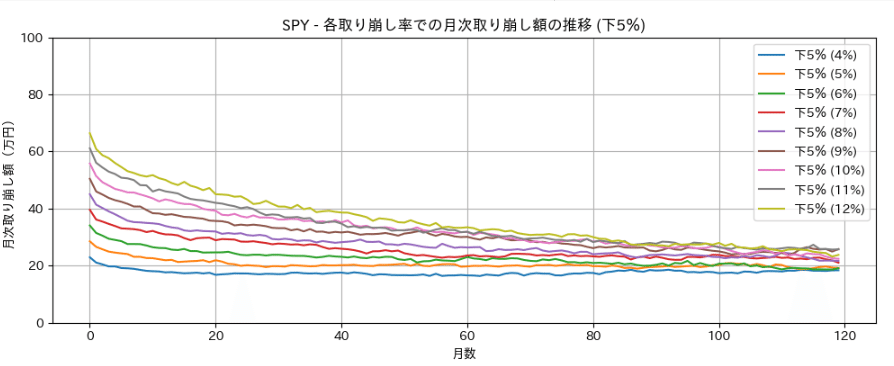
２）追加で確認（実際いくら？？）
　以上定率取り崩しでの最終資産は理解できたと思いますが、具体的に月々の取り崩し額がいくらになるのかきになると思います。
そこで、先ほどのコードで取り崩した場合の月々の資産額の推移を、中央値と、下位５％の場合で出力してみました。（コード全文は本文最下段にあります。）
　実行した結果、中央値であればかなりの額が取り崩しが可能であり、特にリターンが優れるＱＱＱでは初期額７０００万円あれば月々８０万円取り崩しても資産が増える結果です。
逆に下位５％では、月々２０万円程度と、世間一般でいわれる４％取り崩しルールの妥当性を感じる結果です。ぜひ皆様も自分の老後やＦＩＲＥ生活に当てはめて結果をみてもらたらと思います。　

定率取り崩し時の取り崩し額（中央値）

定率取り崩し時の取り崩し額（下位５％）

４　最後に

今回は定率取り崩し額による元本割れを一括で可視化する方法について紹介してみましたがいかがだったでしょうか？
巷で言われる４％ルールというものが体感できたのではないでしょうか。今後も投資リテラシー向上＆プログラミングでできることを発信していきます。応援よろしくお願いします。

記事の感想、要望があれば下記X（旧Twitterまで）
＊今後の記事に活用させていただきます！！

Tweets by KotaKota978293

---

以下、過去記事、AI時系列予測等のご紹介
他サイトですがココならで、A I（LSTM）を使った株価予測の販売もやってます。こちらではFREDから、失業率や２年１０年金利、銅価格等結果も取得しLSTMモデルで予測するコードとなってますので興味があれば見てみてください。またその他２件も米国株投資とは直接関係はありませんがプログラム入門におすすめです。

APPLE（変更可）米株価予測コード販売します AI・LSTMモデルで5日後を予測するpythonコード | 株式・各種投資の相談 | ココナラ

機械学習・重回帰分析　おすすめプログラム販売します 散布図（回帰式、相関係数、P値）・重回帰分析（特徴量評価） | 機械学習 | ココナラ

機械学習LightGBM コード販売します Deep Learning, 特徴量解析，SHAP値 | 機械学習 | ココナラ

---

チャンネル紹介：Kota＠Python＆米国株投資チャンネル

Kota＠Python＆米国株投資チャンネル｜note

過去の掲載記事：興味PYがあればぜひ読んでください。
グラフ化集計の基礎：S &P500と金や米国債を比較してます。

移動平均を使った時系列予測

---

コード全文：