
eMAXIS NASDAQ100 手数料 0.2%違うとどうなる?
サブテーマ:資産形成から取り崩し期の一括シミュレーションで差を確認
1 初めに
最近、eMAXIS NASDAQ100インデックス投資信託の信託手数料をライバルニッセイNASDAQ100並に値下げ(年率0.44→0.2035%)に下げるというニュースを受け、0.2%の差ってどうなの??と気になる方も多いのではと思います。
そこで今回は過去とは違う、手数料の評価ということで、積立期から定年もしくはFIRE後の取り崩し期までの一括シミュレーションできるコードで比較してみます。
投資信託手数料0.2%の違いに興味のある方、その解析方法に興味のある方ぜひ読んでみてください。
今回の結論:
・手数料年率0.2%の差は軽微(アセットの違いの差の方が大きい)
・NASDAQ100を今回の条件で投資すると、95%の確率で
元本30万円/月取り崩しても資産が減らない。
今回のシミュレーション条件:
initial_investment = 200 # 初期投資額(万円)
monthly_investment = 10 # 月次積立額(万円)
investment_duration = 360 # 投資期間(月)
withdrawal_start_month = 240 # 取崩開始月(月数)
withdrawal_amount = 30 # 月次取り崩し額(万円)
simulations = 100 # シミュレーション回数
知人よりプログラム部分が難しくてよくわからないとご指摘をいただきました。そのためこのチャンネルでは、PYTHONを使った米国株投資に関わるさまざまな調査の結果OUTPUTにこだわった記事にします。投資に関わる身近な疑問にも答えていきますので、投資リテラシー向上にお役立ちを目指します!!
なお、全ての解析データは引き続き、PYTHONを活用してコード全文も掲載します。Googleコラボならまずは”コピペ”でチャレンジできます。これから勉強始めたい方にも、プログラミングで何ができるのかを知る良いチャンスとなればと思っていますので応援お願いします!!
2 豆知識
1)投資信託:eMAXIS NASDAQ100インデックス
三井UFJアセットマネジメントのNASDAQ100インデックスに連動する投資信託です。NASDAQ100インデックスに連動する投資信託はニッセイ、楽天、大和アセットマネジメント各社から販売されていますが、ニッセイの投資信託が、販売網が広く手数料が安かったこともあり人気です。
なお、信託報酬引き下げ実施のお知らせについても、上記リンクでPDFファイルを確認することができますので、興味のある方は見てみてください。
参考)ライバルのニッセイの投資信託
3 実践
1)調査内容
今回は、2014年1月から過去20年のNASDAQ100の株価を取得し、0.2%の違いということでリターンを0.2%減らした(=リターンが0.2%分低い)2つで評価しました。
NASDAQ100 →年率リターン0.140%
NASDAQ100+販売手数料0.2% →年率リターン0.138%
また比較のため、S&P500と、シャープレシオが最も良い効率的ポートフォリオである計算させた金(ティッカーGLD)30%、長期米国債(ティッカーTLT)10%残りNASDAQ100のポートフォリオも合わせて同じシミュレーションで比較しています。
シミュレーションはそれぞれの年率リターンとリスクからモンテカルロシミュレーションで積立期から取り崩しにかけて一連のシミュレーションできるコードとしました。これら設定の箇所は下記です。この部分を変更し実行することで簡単に違う条件でシミュレーションすることができます。
# パラメータ設定
initial_investment = 200 # 初期投資額(万円)
monthly_investment = 10 # 月次積立額(万円)
investment_duration = 360 # 投資期間(月)
withdrawal_start_month = 240 # 取崩開始月(月数)
withdrawal_amount = 30 # 月次取り崩し額(万円)
simulations = 100 # シミュレーション回数
2)データの取得とリスク、リターンの算出
データの取得はYahoo Financeから取得し、それぞれリスクとリターンを計算させています。ついでに効率化ポートフォリオを計算させそれぞれテーブルとして結果を出力させます。(時系列グラフ、相関係数も合わせて出力されるコードになっていますので、興味がありました過去記事も是非みてみてください。)
pip install japanize-matplotlib
!pip install PyPortfolioOpt
# 必要なライブラリのインポート
import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import japanize_matplotlib # 日本語表示に対応
from pypfopt import expected_returns, risk_models, EfficientFrontier, plotting
# 対象のティッカーシンボル
tickers = ['SPY', 'QQQ','TLT','GLD']
# データの取得
data = yf.download(tickers, start="2004-01-01", end=pd.Timestamp.now().strftime('%Y-%m-%d'))['Adj Close']
# Monthly resampling to get the first data point of each month
monthly_data = data.resample('MS').first()
# 1. Time series line graph
plt.figure(figsize=(12, 5))
for ticker in monthly_data.columns:
plt.plot(monthly_data[ticker], label=ticker)
plt.title('月次調整後終値の時間推移')
plt.xlabel('日付')
plt.ylabel('調整後終値')
plt.legend()
# Normalize data
normalized_data = monthly_data.apply(lambda x: x / x.iloc[0] * 100)
# 2. Time series graph of normalized data
plt.figure(figsize=(12, 5))
for ticker in normalized_data.columns:
plt.plot(normalized_data[ticker], label=ticker)
plt.axhline(y=100, color='red', linestyle='--', linewidth=1)
plt.title('正規化された月次調整後終値の時間推移')
plt.xlabel('日付')
plt.ylabel('正規化価格 (基準=100)')
plt.legend()
# 3. Log-scale graph of normalized data
plt.figure(figsize=(12, 5))
for ticker in normalized_data.columns:
plt.plot(normalized_data[ticker], label=ticker)
plt.axhline(y=100, color='red', linestyle='--', linewidth=1)
plt.title('対数スケールにおける正規化された月次調整後終値の時間推移')
plt.xlabel('日付')
plt.ylabel('対数正規化価格 (基準=100)')
plt.legend()
plt.yscale('log')
plt.show()
# 日次リターンの計算
daily_returns = data.pct_change()
# SPYに対する相関係数を計算
correlations = daily_returns.corr().loc['SPY']
# 月次リターンの計算
monthly_data = data.resample('M').last()
monthly_returns = monthly_data.pct_change().dropna()
# 年化された期待リターンとリスク(共分散行列)の計算
mean_returns = expected_returns.mean_historical_return(monthly_data, frequency=12)
cov_matrix = risk_models.sample_cov(monthly_data, frequency=12)
# 各ティッカーのリスク(標準偏差)とリターンの計算
individual_risks = np.sqrt(np.diag(cov_matrix))
individual_returns = mean_returns.values
# 最適化:シャープレシオを最大化
ef = EfficientFrontier(mean_returns, cov_matrix)
weights = ef.max_sharpe()
cleaned_weights = ef.clean_weights()
# 最適化されたポートフォリオのパフォーマンス計算
expected_return, volatility, sharpe_ratio = ef.portfolio_performance(verbose=True)
# 効率的フロンティアの点を生成
ef_new = EfficientFrontier(mean_returns, cov_matrix)
fig, ax = plt.subplots(1, 3, figsize=(18, 6))
# 散布図と効率的フロンティア
ax[0].scatter(volatility, expected_return, color='red', s=100, label='最適化されたポートフォリオ')
ax[0].scatter(individual_risks, individual_returns, color='blue', s=50) # 各ティッカー
for i, txt in enumerate(mean_returns.index):
ax[0].annotate(txt, (individual_risks[i], individual_returns[i]))
plotting.plot_efficient_frontier(ef_new, ax=ax[0], show_assets=True)
ax[0].set_title('ポートフォリオおよび各ティッカーのリスクとリターン')
ax[0].set_xlabel('標準偏差(リスク)')
ax[0].set_ylabel('期待リターン')
ax[0].grid(True)
ax[0].legend()
# ウェイトの棒グラフ
ax[1].bar(cleaned_weights.keys(), cleaned_weights.values(), color='green')
ax[1].set_title('ポートフォリオの最適化されたウェイト')
ax[1].set_xlabel('資産')
ax[1].set_ylabel('ウェイト')
ax[1].grid(True)
# SPYとの相関係数の棒グラフ
correlation_values = correlations.drop('SPY')
ax[2].bar(correlation_values.index, correlation_values.values, color='purple')
ax[2].set_title('S&P500との相関係数')
ax[2].set_xlabel('資産')
ax[2].set_ylabel('相関係数')
ax[2].grid(True)
plt.tight_layout()
plt.show()
# 最大ドローダウンの計算
def calculate_max_drawdown(returns):
cumulative = (1 + returns).cumprod()
drawdown = (cumulative / cumulative.cummax()) - 1
return drawdown.min()
# ポートフォリオのパフォーマンス指標の表示
portfolio_performance = pd.DataFrame({
'ティッカー': tickers,
'年率リターン': [mean_returns.loc[ticker] for ticker in tickers],
'年率リスク': [cov_matrix.loc[ticker, ticker] ** 0.5 for ticker in tickers],
'シャープレシオ': [mean_returns.loc[ticker] / (cov_matrix.loc[ticker, ticker] ** 0.5) for ticker in tickers],
'最大ドローダウン': [calculate_max_drawdown(daily_returns[ticker]) for ticker in tickers]
})
# ポートフォリオの累積リターンを計算
portfolio_cumulative_return = (1 + daily_returns.dot(pd.Series(cleaned_weights))).cumprod()
portfolio_drawdown = (portfolio_cumulative_return / portfolio_cumulative_return.cummax()) - 1
max_drawdown = portfolio_drawdown.min()
# 最適化されたポートフォリオのパフォーマンス指標の追加
optimized_performance = pd.DataFrame({
'ティッカー': ['最適化されたポートフォリオ'],
'年率リターン': [expected_return],
'年率リスク': [volatility],
'シャープレシオ': [sharpe_ratio],
'最大ドローダウン': [max_drawdown]
})
# 結果を結合
portfolio_performance = pd.concat([portfolio_performance, optimized_performance], ignore_index=True)
portfolio_performance.set_index('ティッカー', inplace=True)
# 小数点以下3桁に丸める
portfolio_performance = portfolio_performance.round(3)
portfolio_performance

3)積立期から取り崩し期までのシミュレーション
先ほどのコードで得られたリターンとリスクを用いて実際にシミュレーションします。積立額、取り崩し額やその期間をそれぞれ変更することで自分なりのシミュレーションが可能です。
# 必要なライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
initial_investment = 200 # 初期投資額(万円)
monthly_investment = 10 # 月次積立額(万円)
investment_duration = 360 # 投資期間(月)
withdrawal_start_month = 240 # 取崩開始月(月数)
withdrawal_amount = 30 # 月次取り崩し額(万円)
simulations = 100 # シミュレーション回数
# tickersリストを定義
tickers = ['S&P500', 'NASDAQ100', 'NASDAQ100+0.2%', 'Balanced Portfolio']
# 年次リターンと年次標準偏差(手動設定)
annual_returns = {'S&P500': 0.099, 'NASDAQ100': 0.140, 'NASDAQ100+0.2%': 0.138, 'Balanced Portfolio': 0.112}
annual_std_devs = {'S&P500': 0.149, 'NASDAQ100': 0.184, 'NASDAQ100+0.2%': 0.184, 'Balanced Portfolio': 0.124}
# 年次リターンと年次標準偏差を月次リターンへ変換
monthly_returns = {ticker: (1 + annual_returns[ticker])**(1/12) - 1 for ticker in tickers}
monthly_std_devs = {ticker: annual_std_devs[ticker] / np.sqrt(12) for ticker in tickers}
# 各シミュレーションの資産額を保存する配列の初期化
all_time_series = []
for ticker in tickers:
monthly_return_mean = monthly_returns[ticker]
monthly_return_std = monthly_std_devs[ticker]
# この配列に各シミュレーションの時系列データを保存
time_series_simulations = np.zeros((simulations, investment_duration))
for simulation in range(simulations):
total_value = initial_investment
for month in range(investment_duration):
monthly_return = np.random.normal(monthly_return_mean, monthly_return_std)
if month < withdrawal_start_month:
# 資産形成期
total_value = total_value * (1 + monthly_return) + monthly_investment
else:
# 取崩し期
total_value = total_value * (1 + monthly_return) - withdrawal_amount
# 各月の資産額を保存
time_series_simulations[simulation, month] = max(total_value, 0) # 資産額が0未満にならないようにする
all_time_series.append(time_series_simulations)
fig, axes = plt.subplots(nrows=len(tickers), ncols=1, figsize=(10, 3 * len(tickers)))
axes = axes.flatten() if len(tickers) > 1 else [axes]
# y軸の上限を設定
y_max = (initial_investment + monthly_investment * withdrawal_start_month) * 8
for i, ticker in enumerate(tickers):
ax = axes[i]
time_series_simulations = all_time_series[i]
# 中央値、下5%、上95%の計算
median_values = np.median(time_series_simulations, axis=0)
percentile_5 = np.percentile(time_series_simulations, 5, axis=0)
percentile_95 = np.percentile(time_series_simulations, 95, axis=0)
# 各シミュレーションの時系列データをプロット
for simulation in range(simulations):
ax.plot(range(investment_duration), time_series_simulations[simulation], alpha=0.2, color='blue')
# 中央値、下5%、上95%のプロット
ax.plot(range(investment_duration), median_values, color='green', label='中央値', linewidth=2)
ax.plot(range(investment_duration), percentile_5, color='orange', linestyle='--', label='下5%')
ax.plot(range(investment_duration), percentile_95, color='purple', linestyle='--', label='上95%')
# 元本の推移をプロット(黒の点線)
total_principal_over_time = np.concatenate([
initial_investment + np.arange(withdrawal_start_month) * monthly_investment,
[initial_investment + monthly_investment * withdrawal_start_month - withdrawal_amount * (i - withdrawal_start_month) for i in range(withdrawal_start_month, investment_duration)]
])
ax.plot(total_principal_over_time, color='black', linestyle=':', label='元本の推移')
# 縦線を追加(積立期と取り崩し期の境界)
ax.axvline(x=withdrawal_start_month, color='red', linestyle='--', label='取崩し開始')
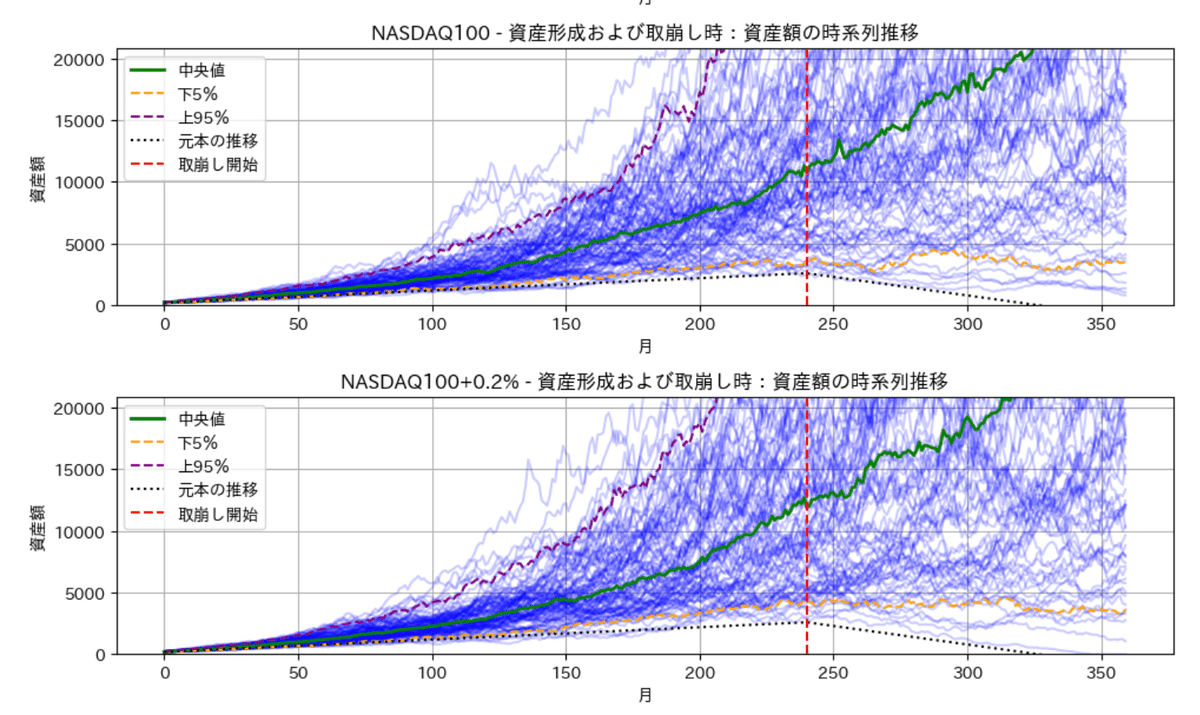
ax.set_title(f'{ticker} - 資産形成および取崩し時:資産額の時系列推移')
ax.set_xlabel('月')
ax.set_ylabel('資産額')
ax.legend()
ax.grid(True)
# すべてのサブプロットのy軸の範囲を設定
ax.set_ylim([0, y_max])
plt.tight_layout()
plt.show()
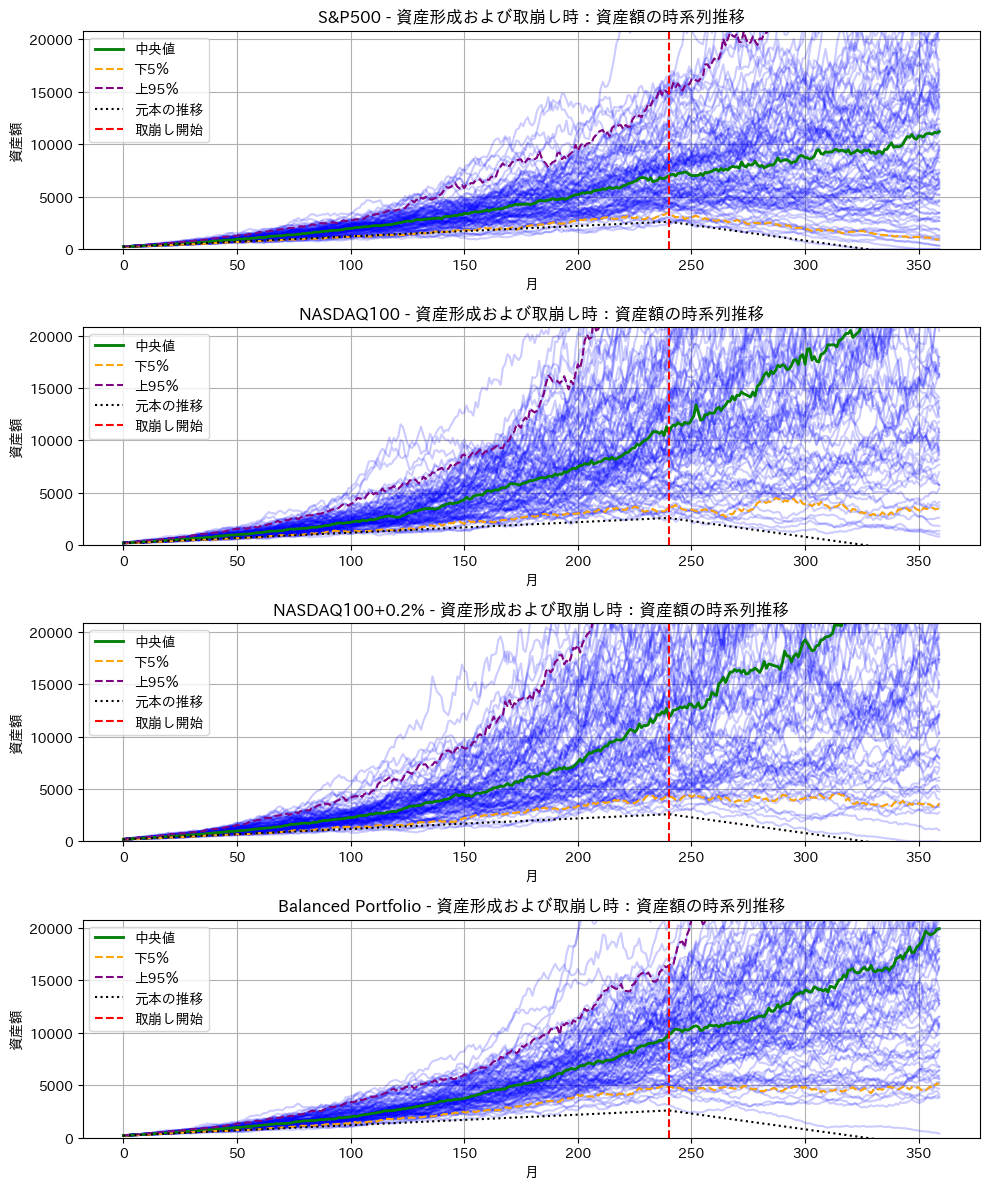
最上段)SP500、NASDAQ100、NASDAQ100+手数料0.2%、最適化ポートフォリオ(下段)
実行した結果の2段目と3段目がNADAQ100の手数料0.2%の違いですが、はっきり言って違いはないかと思います。厳密に見れば違いはありますが、その違いはSP500や最適化ポートフォリオほどの違いはありません。
それ以外に、黒の点線が元本ですが、どのパターンでも100回に1回も取り崩し期のマイナスはありません。
加えて、95%以上の確率で取り崩し期でも資産の減少少なく月30万円が受け取れています。以上のことをまとめると下記の通りです。
まとめ
今回のシミュレーション条件:
initial_investment = 200 # 初期投資額(万円)
monthly_investment = 10 # 月次積立額(万円)
investment_duration = 360 # 投資期間(月)
withdrawal_start_month = 240 # 取崩開始月(月数)
withdrawal_amount = 30 # 月次取り崩し額(万円)
simulations = 100 # シミュレーション回数
・手数料年率0.2%の差は軽微(アセットの違いの差の方が大きい)
・NASDAQ100を今回の条件で投資すると、95%の確率で
元本30万円/月取り崩しても資産が減らない。
4 最後に
今回は、手数料に注目したNASDAQ100のシミュレーションを実施してみました。PYTHONを使えば、銘柄だけでなく、手数料の違い、他のアセットとの違いをお好みの条件で手軽に比較できることもお伝えできていたら幸いです。
今後も投資リテラシー向上兼プログラム活用に役立つ情報を発信していきますので応援のほどよろしくお願いします!
*過去20年の実績をもとにシミュレーションした結果です。今後の結果を保証するものではありません。実際の投資判断はご自身にてお願いいたします。
記事の感想、要望があれば下記X(旧Twitterまで)
*今後の記事に活用させていただきます!!
以下、過去記事、AI時系列予測等のご紹介
他サイトですがココならで、A I(LSTM)を使った株価予測の販売もやってます。こちらではFREDから、失業率や2年10年金利、銅価格等結果も取得しLSTMモデルで予測するコードとなってますので興味があれば見てみてください。またその他2件も米国株投資とは直接関係はありませんがプログラム入門におすすめですのでみてみてください。
チャンネル紹介:Kota@Python&米国株投資チャンネル
過去の掲載記事:興味があればぜひ読んでください。
グラフ化集計の基礎:S &P500と金や米国債を比較してます。
移動平均を使った時系列予測
