
S&P500Top10vsFANG+どっち買う
サブテーマ:Tracers投資信託S&P500TOP10インデックスは買いか?!
1 初めに
今回は、新しい投資信託「Tracers S&P500トップ10インデックス」以下S P500T10が販売開始になるというニュースを受け、新NISAで購入しているFANG+から乗り換えるかどうか検討してみました。
コード自体は、前回とほぼ同じですが、PYTHONの活用法としても読んで頂けると幸いです。
今回の結論:過去10年間での比較
比較対象:SP500(VOO)、NASDAQ100(QQQ)、SP500T10、FANG+
①リターン:良 FANG+>>QQQ≧SP500T10>>SP500
②資産形成期: リターン重視:FANG+
取崩期 : SP500の一部にSP500T10組入も候補の一つ

知人よりプログラム部分が難しくてよくわからないとご指摘をいただきました。そのためこのチャンネルでは、PYTHONを使った米国株投資に関わるさまざまな調査の結果OUTPUTにこだわった記事にします。投資に関わる身近な疑問にも答えていきますので、投資リテラシー向上にお役立ちを目指します!!
なお、全ての解析データは引き続き、PYTHONを活用してコード全文も掲載します。Googleコラボならまずは”コピペ”でチャレンジできます。これから勉強始めたい方にも、プログラミングで何ができるのかを知る良いチャンスとなればと思っていますので応援お願いします!!
2 豆知識
1)投資信託:SP500Top10インデックスとは?

https://www.nikkoam.com/files/lists/news/2024/news0501_01.pdf

2024年5月16日から日興アセットマネジメント株式会社から募集開始となる投資信託です。S&P500トップ10指数とは、S&P500指数の構成銘柄のうち、時価総額上位10社の株式で構成される株価指数です。同指数は、浮動株調整後の時価総額を加重平均して算出されます。 原則として毎年6月に構成銘柄の見直しが実施され、年4回、構成比率の調整が行なわれます。構成銘柄は上記の通りです。信託報酬もカタログ値上は0.1%程度と安いことも大きな特徴です。
2)投資信託:FANG+とは?

この記事のでのFANG+とは、大和アセットマネジメントから販売されている下記の10社に均等投資するFANG+株価指数に連動する投資信託です。特徴はホームページやその他のインフルエンサーがよりわかりやすくまとめられていますので詳しくはそちらをみてもらえればと思いますが、私自身の一番の特徴は、つみたてNISA対象であることです。世界のテクノロジー分野TOP 10に新NISAのつみたて枠で集中投資するならこれ一択です。
3 実践
1)調査内容
今回、S&P500トップ10インデックスとFANG+を比較しますが、さらに比較として、S &P500に連動するETF(VOO)、NASDAQ100に連動するETF(QQQ)と比較します。これら過去10年のデータから、トレンドグラフ、リターンとリスク、シャープレシオ、最大ドローダウン、S&P500との相関係数を調査します。また積立期、取崩期のシミュレーションで優位差を確認しました。
2)データ取得と時系列グラフのプロット
S&P500トップ10インデックスの過去データは下記の海外サイトからEXCLE形式入手しました(リンクは下記)。
https://www.spglobal.com/spdji/en/indices/equity/sp-500-top-10-index/#overview
このデータをCSVに加工し、GoogleColabで取り込みました。Yahoo Financeから2014年からの株価データを一括取得していますが、比較した中でFANG+のインデックス指数が同年9月22日以降のデータのためデータのスタートはFANG+に合わせてます。これら時系列にプロットしますが、変化率と増減が明確になるよう対数軸メモリとしたグラフをプロットします。
pip install japanize-matplotlib
!pip install ffn
!pip install PyPortfolioOpt
#GoogleDriveに接続
from google.colab import drive
drive.mount('/content/drive')
import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import japanize_matplotlib # 日本語表示に対応
# 対象のティッカーシンボル
tickers = ['VOO', 'QQQ','^NYFANG']
# データの取得
data = yf.download(tickers, start="2014-01-01", end=pd.Timestamp.now().strftime('%Y-%m-%d'))['Adj Close']
# Google Driveからデータを取得
sp500_data = pd.read_csv('/content/drive/MyDrive/SP500T10.csv', parse_dates=[0], index_col=0)
# データ結合
data = pd.concat([data, sp500_data.rename(columns={"Adj Close": "SP500T10"})], axis=1).dropna()
# 月データに変換
monthly_data = data.resample('MS').first()
# 正規化
normalized_data = monthly_data.apply(lambda x: x / x.iloc[0] * 100)
# 対数軸の正規化した時系列グラフ
plt.figure(figsize=(12, 5))
for ticker in normalized_data.columns:
plt.plot(normalized_data[ticker], label=ticker)
plt.axhline(y=100, color='red', linestyle='--', linewidth=1)
plt.title('対数スケールにおける正規化された月次調整後終値の時間推移')
plt.xlabel('日付')
plt.ylabel('対数正規化価格 (基準=100)')
plt.legend()
plt.yscale('log')
plt.show()
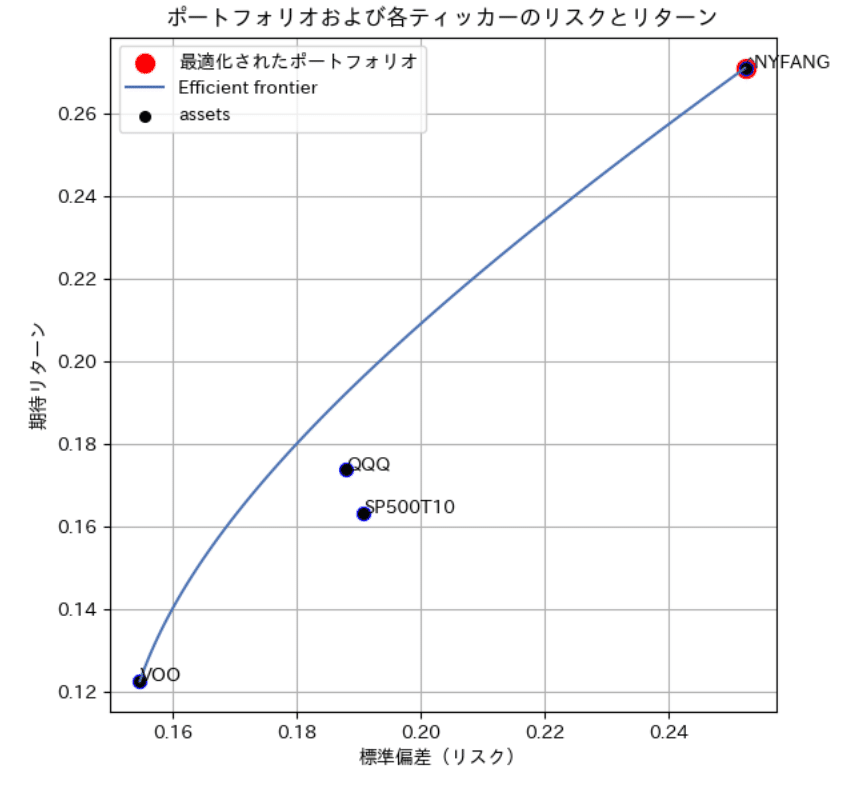
時系列チャートでの比較の結果が実力をよく表していて、SP500T10はQQQ相当のリターンが見込める結果です。その他指標については次で細かく確認します。
3)リスク&リターンの算出、効率化フロンティア曲線の作図
いよいよ本番ですが、コードとしては下記だけですので、コピペで簡単に実行できます。リターン・リスク(標準偏差)の計算、シャープレシオの計算、効率化フロンティアの曲線の作図、相関係数の確認が可能です。
from pypfopt import expected_returns, risk_models, EfficientFrontier, plotting
# 日次リターンの計算
daily_returns = data.pct_change()
# SPYに対する相関係数を計算
correlations = daily_returns.corr().loc['VOO']
# 月次リターンの計算
monthly_data = data.resample('M').last()
monthly_returns = monthly_data.pct_change().dropna()
# 年化された期待リターンとリスク(共分散行列)の計算
mean_returns = expected_returns.mean_historical_return(monthly_data, frequency=12)
cov_matrix = risk_models.sample_cov(monthly_data, frequency=12)
# 各ティッカーのリスク(標準偏差)とリターンの計算
individual_risks = np.sqrt(np.diag(cov_matrix))
individual_returns = mean_returns.values
# 最適化:シャープレシオを最大化
ef = EfficientFrontier(mean_returns, cov_matrix)
weights = ef.max_sharpe()
cleaned_weights = ef.clean_weights()
# 最適化されたポートフォリオのパフォーマンス計算
expected_return, volatility, sharpe_ratio = ef.portfolio_performance(verbose=True)
# 効率的フロンティアの点を生成
ef_new = EfficientFrontier(mean_returns, cov_matrix)
fig, ax = plt.subplots(1, 3, figsize=(18, 6))
# 散布図と効率的フロンティア
ax[0].scatter(volatility, expected_return, color='red', s=100, label='最適化されたポートフォリオ')
ax[0].scatter(individual_risks, individual_returns, color='blue', s=50) # 各ティッカー
for i, txt in enumerate(mean_returns.index):
ax[0].annotate(txt, (individual_risks[i], individual_returns[i]))
plotting.plot_efficient_frontier(ef_new, ax=ax[0], show_assets=True)
ax[0].set_title('ポートフォリオおよび各ティッカーのリスクとリターン')
ax[0].set_xlabel('標準偏差(リスク)')
ax[0].set_ylabel('期待リターン')
ax[0].grid(True)
ax[0].legend()
# ウェイトの棒グラフ
ax[1].bar(cleaned_weights.keys(), cleaned_weights.values(), color='green')
ax[1].set_title('ポートフォリオの最適化されたウェイト')
ax[1].set_xlabel('資産')
ax[1].set_ylabel('ウェイト')
ax[1].grid(True)
# SPYとの相関係数の棒グラフ
correlation_values = correlations.drop('VOO') # VOO自体の相関は除外
ax[2].bar(correlation_values.index, correlation_values.values, color='purple')
ax[2].set_title('S&P500との相関係数')
ax[2].set_xlabel('資産')
ax[2].set_ylabel('相関係数')
ax[2].grid(True)
plt.tight_layout()
plt.show()
import ffn # このライブラリを使用して最大ドローダウンを計算
# 年次リターン、標準偏差、シャープレシオ、最大ドローダウンを計算
results = []
for ticker in tickers:
# ティッカーごとの月次クローズ価格
prices = monthly_data[ticker].dropna()
# 月次リターンの計算
monthly_returns = ffn.to_returns(prices).dropna()
# 年次リターンの計算(月次リターンの平均 * 12)
annual_return = monthly_returns.mean() * 12
# 年次標準偏差の計算(月次ボラティリティ * sqrt(12))
annual_vol = monthly_returns.std() * np.sqrt(12)
# シャープレシオ
sharpe_ratio = annual_return / annual_vol
# 最大ドローダウン
max_drawdown = ffn.calc_max_drawdown(prices)
results.append({
"Ticker": ticker,
"Annual Return": annual_return,
"Annual Volatility": annual_vol,
"Sharpe Ratio": sharpe_ratio,
"Max Drawdown": max_drawdown
})
# DataFrameに変換して表示
results_df = pd.DataFrame(results)
results_df.set_index('Ticker', inplace=True)
#結果の表示
results_df
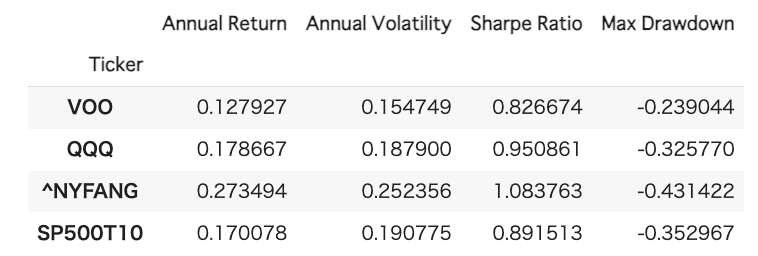
結果まとめ
リターン:良 FANG+>>QQQ≧SP500T10>>SP500
効率化フロンティア曲線&最適ポートフォリオ:FANG+100%
最大ドローダウン: 悪 FANG+>>QQQ≧SP500T10>>SP500 良
相関係数(SP500): 高 QQQ=S P500T10> FANG+
3)シミュレーションで確認
資産形成期として元本200万円+毎月3万円を30年積立したシミュレーションです。コードはほぼ前回と同じです。
# 必要なライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# パラメータ設定
initial_investment = 200 # 初期投資額(200万円)
monthly_investment = 3 # 月次積立額(3万円)
investment_duration = 360 # 投資期間(月)
simulations = 100 # シミュレーション回数
# tickersリストを定義
tickers = [ 'S&P500', 'S&P500TOP10', 'FANG+', 'NASDAQ100']
# 年次リターンと年次標準偏差(手動設定)
annual_returns = {'S&P500': 0.128, 'S&P500TOP10': 0.170, 'FANG+': 0.273, 'NASDAQ100': 0.179}
annual_std_devs = {'S&P500': 0.155, 'S&P500TOP10': 0.191, 'FANG+': 0.252, 'NASDAQ100': 0.188}
# 年次リターンと年次標準偏差を月次リターンへ変換
monthly_returns = {ticker: (1 + annual_returns[ticker])**(1/12) - 1 for ticker in tickers}
monthly_std_devs = {ticker: annual_std_devs[ticker] / np.sqrt(12) for ticker in tickers}
# 各シミュレーションの資産額を保存する配列の初期化
all_time_series = []
for ticker in tickers:
monthly_return_mean = monthly_returns[ticker]
monthly_return_std = monthly_std_devs[ticker]
# この配列に各シミュレーションの時系列データを保存
time_series_simulations = np.zeros((simulations, investment_duration))
for simulation in range(simulations):
total_value = initial_investment
for month in range(investment_duration):
monthly_return = np.random.normal(monthly_return_mean, monthly_return_std)
total_value = total_value * (1 + monthly_return) + monthly_investment
# 各月の資産額を保存
time_series_simulations[simulation, month] = total_value
all_time_series.append(time_series_simulations)
fig, axes = plt.subplots(nrows=len(tickers), ncols=1, figsize=(10, 3 * len(tickers)))
axes = axes.flatten() if len(tickers) > 1 else [axes]
# y軸の上限を設定
y_max = (initial_investment + monthly_investment * investment_duration) * 5
for i, ticker in enumerate(tickers):
ax = axes[i]
time_series_simulations = all_time_series[i]
# 中央値、下5%、上95%の計算
median_values = np.median(time_series_simulations, axis=0)
percentile_5 = np.percentile(time_series_simulations, 5, axis=0)
percentile_95 = np.percentile(time_series_simulations, 95, axis=0)
# 各シミュレーションの時系列データをプロット
for simulation in range(simulations):
ax.plot(range(investment_duration), time_series_simulations[simulation], alpha=0.2, color='blue')
# 中央値、下5%、上95%のプロット
ax.plot(range(investment_duration), median_values, color='green', label='中央値', linewidth=2)
ax.plot(range(investment_duration), percentile_5, color='orange', linestyle='--', label='下5%')
ax.plot(range(investment_duration), percentile_95, color='purple', linestyle='--', label='上95%')
# 元本の推移をプロット(黒の点線)
total_principal_over_time = initial_investment + np.arange(investment_duration) * monthly_investment
ax.plot(total_principal_over_time, color='black', linestyle=':', label='元本の推移')
ax.set_title(f'{ticker} - 一括&積立時:資産額の時系列推移')
ax.set_xlabel('月')
ax.set_ylabel('資産額')
ax.legend()
ax.grid(True)
# すべてのサブプロットのy軸の範囲を設定
ax.set_ylim([0, y_max])
plt.tight_layout()
plt.show()
積立期:良 FANG+>>QQQ≧SP500T10>>SP500 悪
次に、初期投資5000万円で年間300万円定額取崩した場合の取崩期のシミュレーションです。同じくコードは前回と同じです。
# 必要なライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# パラメータ設定
initial_investment = 5000 # 初期投資額(5000万円)
withdrawal_amount = 300 # 年次取り崩し額(300万円)
investment_duration = 10 # 投資期間(年)
simulations = 100 # シミュレーション回数
# tickersリストを定義
tickers = [ 'S&P500', 'S&P500TOP10', 'FANG+', 'NASDAQ100']
# 年次リターンと年次標準偏差(手動設定)
annual_returns = {'S&P500': 0.128, 'S&P500TOP10': 0.170, 'FANG+': 0.273, 'NASDAQ100': 0.179}
annual_std_devs = {'S&P500': 0.155, 'S&P500TOP10': 0.191, 'FANG+': 0.252, 'NASDAQ100': 0.188}
# 各シミュレーションの資産額を保存する配列の初期化
all_time_series = []
for ticker in tickers:
annual_return_mean = annual_returns[ticker]
annual_return_std = annual_std_devs[ticker]
# この配列に各シミュレーションの時系列データを保存
time_series_simulations = np.zeros((simulations, investment_duration))
for simulation in range(simulations):
total_value = initial_investment
for year in range(investment_duration):
annual_return = np.random.normal(annual_return_mean, annual_return_std)
total_value = total_value * (1 + annual_return) - withdrawal_amount
# 各年の資産額を保存
time_series_simulations[simulation, year] = max(total_value, 0)
all_time_series.append(time_series_simulations)
fig, axes = plt.subplots(nrows=4, ncols=1, figsize=(10, 14))
axes = axes.flatten()
# y軸の上限を設定
y_max = initial_investment * 5
for i, ticker in enumerate(tickers):
ax = axes[i]
time_series_simulations = all_time_series[i]
# 中央値、上5%、下5%の計算
median_values = np.median(time_series_simulations, axis=0)
percentile_95 = np.percentile(time_series_simulations, 95, axis=0)
percentile_5 = np.percentile(time_series_simulations, 5, axis=0)
# 各シミュレーションの時系列データをプロット
for simulation in range(simulations):
ax.plot(range(investment_duration), time_series_simulations[simulation], alpha=0.2, color='blue')
# 中央値、上5%、下5%のプロット
ax.plot(range(investment_duration), median_values, color='green', label='中央値', linewidth=2)
ax.plot(range(investment_duration), percentile_95, color='orange', label='上5%', linestyle='--')
ax.plot(range(investment_duration), percentile_5, color='purple', label='下5%', linestyle='--')
# 元本の線を黒の点線で追加
ax.axhline(y=initial_investment, color='black', linestyle=':', label='元本')
ax.set_title(f'{ticker} - 取崩時:資産額の時系列推移')
ax.set_xlabel('年')
ax.set_ylabel('資産額')
ax.legend()
ax.grid(True)
# すべてのサブプロットのy軸の範囲を設定
ax.set_ylim([0, y_max])
plt.tight_layout()
plt.show()

結果をまとめるにあたり何を重視するかで結果は変わります。SP500T10は元本割れの確率は、SP500とほぼ同等ですが、中央値はむしろ資産が増加しており、SP500よりはより大きな額が取り崩せる可能性があります。しかし、リータンの優れたFANG+ほどではなく、QQQ程度の実力であると推測されます。
良 FANG+>QQQ≧SP500T10≧SP500 悪
おまけ)
QLD(レバナス相当)やTLT(長期米国債)やGLD(金)とも比較



4 まとめ
今回、ほぼ前回と同じコードですが、面白そうな投資信託が出てきたので評価してみましたが如何でしょうか?
自分自身、SP500とFANG+を新NISAに組み込んでいるのですが、SP500の一部をこのSP500Top10インデックスファンドに変更するのは良い方向なのかと考えてます。
皆様の投資生活のお役に立てれば幸いです。
*今回の結果も、過去10年の実績をもとにシミュレーションした結果です。今後の結果を保証するものではありません。実際の投資判断はご自身にてお願いいたします。
以下、過去記事、AI時系列予測等のご紹介
他サイトですがココならで、A I(LSTM)を使った株価予測の販売もやってます。こちらではFREDから、失業率や2年10年金利、銅価格等結果も取得しLSTMモデルで予測するコードとなってますので興味があれば見てみてください。またその他2件も米国株投資とは直接関係はありませんがプログラム入門におすすめですのでみてみてください。
チャンネル紹介:Kota@Python&米国株投資チャンネル
過去の掲載記事:興味があればぜひ読んでください。
グラフ化集計の基礎:S &P500と金や米国債を比較してます。
移動平均を使った時系列予測
