
Infrequent Metadynamics
本記事ではMetadynamicsを用いて効率的に状態間の(平均)遷移時間を予測する目的で提案されたInfrequent Metadynamicsについて解説します。
"Infrequent"の言葉の通り,Infrequent Metadynamicsは技術的にはバイアスポテンシャルの更新を単にInfrequentにした手法ですが,"Infrequent"であることが本質的に重要な役割を果たします。
問題設定
系の配置自由度を$${\mathbf{R}}$$とし,ポテンシャル$${U(\mathbf{R})}$$の下で運動している状況を考えます。反応座標$${\hat{\lambda}(\mathbf{R})}$$において,系は図1のような形状の自由エネルギー地形を持つとします。2つの状態$${A, B}$$は$${\lambda=\lambda^*}$$にある
自由エネルギー障壁で阻まれており,状態間の遷移はレアイベントです。初期状態は状態$${A}$$にあり,$${A\rightarrow B}$$の(平均)遷移時間を求めることを考えます。
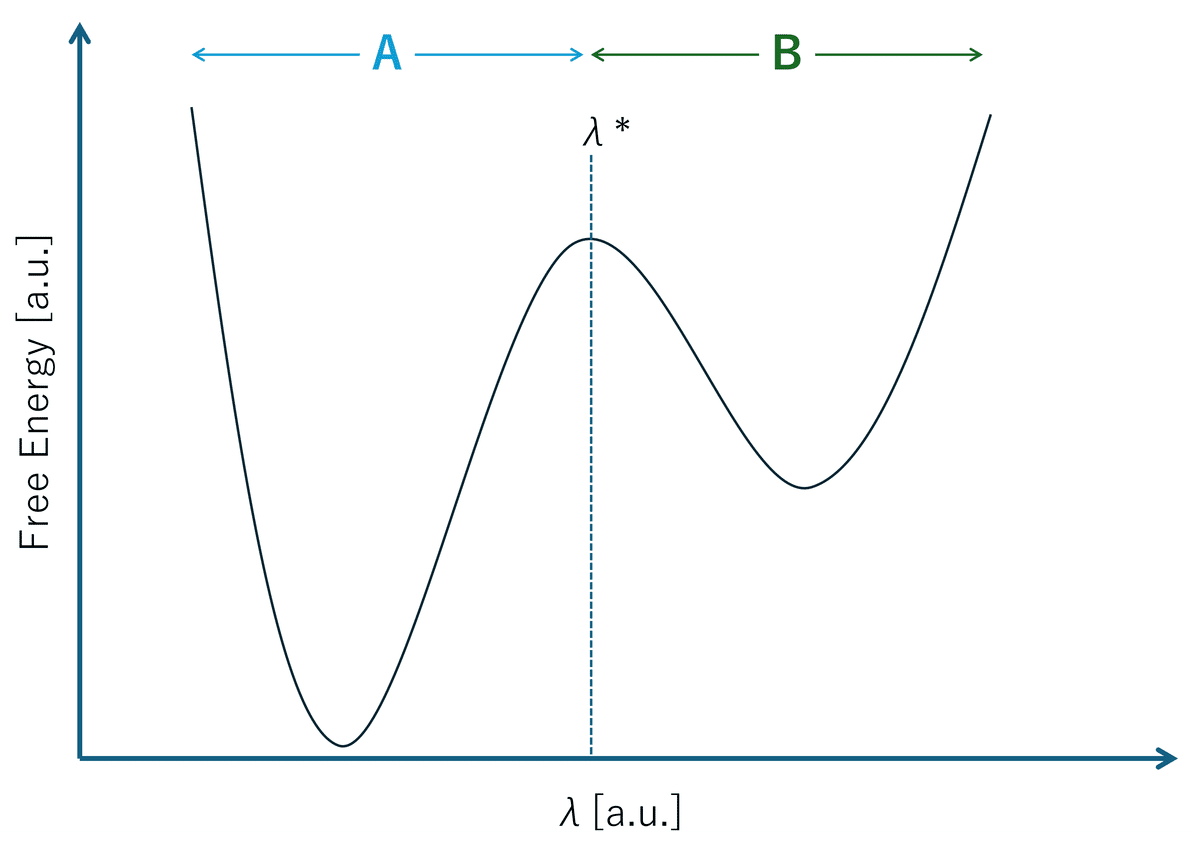
遷移時間と自由エネルギー差の関係
遷移状態理論によると,遷移時間(=遷移率の逆数)$${\tau}$$は状態$${A}$$の自由エネルギー$${G_A}$$と$${\lambda^*}$$における自由エネルギー$${G(\lambda^*)}$$の差で特徴づけることができます。
$$
\begin{align*}
\tau\propto \exp\left(\beta\Delta G\right)=\exp\left(\beta (G(\lambda^*)-G_A)\right)
\end{align*}\tag{1}
$$
ここで,$${\beta}$$は逆温度です。
$${G(\lambda^*)}$$は(2)式で表すことができます。
$$
\begin{align*}
\exp\left(-\beta G(\lambda^*)\right)\propto \int{\rm d}\mathbf{R}\delta\left(\hat{\lambda}(\mathbf{R})-\lambda^*\right)\exp\left(-\beta U(\mathbf{R})\right)
\end{align*}\tag{2}
$$
状態$${A}$$を極小値のみで特徴づけるか,極小値周りをある程度取り込むかは任意性がありますが,実質的には極小値のごく周辺のみしか積分に寄与しないことを考慮し,参考文献1に倣って$${\lambda\le\lambda^*}$$の寄与を取り込むことにします。
$$
\begin{align*}
\exp\left(-\beta G_A\right)\propto \int_{\lambda\le\lambda^*}{\rm d}\lambda\int{\rm d}\mathbf{R}\delta\left(\hat{\lambda}(\mathbf{R})-\lambda\right)\exp\left(-\beta U(\mathbf{R})\right)
\end{align*}\tag{3}
$$
(2), (3)式を(1)式に代入すると(4)式が得られます。
$$
\begin{align*}
\tau&\propto \frac{\int_{\lambda\le\lambda^*}{\rm d}\lambda\int{\rm d}\mathbf{R}\delta\left(\hat{\lambda}(\mathbf{R})-\lambda\right)\exp\left(-\beta U(\mathbf{R})\right)}{\int{\rm d}\mathbf{R}\delta\left(\hat{\lambda}(\mathbf{R})-\lambda^*\right)\exp\left(-\beta U(\mathbf{R})\right)}
\end{align*}\tag{4}
$$
$${\tau}$$は$${\lambda=\lambda^*}$$のrecrossingに由来する輸送係数$${\kappa}$$にも依存します。
$$
\begin{align*}
\tau&\propto \frac{1}{\kappa}
\end{align*}\tag{5}
$$
これは一見奇妙な言及に見えるかもしれませんが,複雑な系の場合,状態間の違いを特徴付ける反応座標を上手く見出せたとしても,その座標にある極大値が物理的に意味のある遷移状態に一致する保証はありません。その結果として,状態遷移するまでに極大値を何回も通る軌道となる可能性があります。
(4),(5)式を合わせ,また規格化定数を$${\omega}$$とすると,
$$
\begin{align*}
\tau&=\frac{1}{\omega\kappa} \frac{\int_{\lambda\le\lambda^*}{\rm d}\lambda\int{\rm d}\mathbf{R}\delta\left(\hat{\lambda}(\mathbf{R})-\lambda\right)\exp\left(-\beta U(\mathbf{R})\right)}{\int{\rm d}\mathbf{R}\delta\left(\hat{\lambda}(\mathbf{R})-\lambda^*\right)\exp\left(-\beta U(\mathbf{R})\right)}
\end{align*}\tag{6}
$$
バイアスポテンシャルによる遷移の加速化
通常のMD(Molecyular Dynamics,分子動力学)計算をひたすら流して$${A\rightarrow B}$$の遷移を観測することで遷移時間$${\tau}$$を見積もることは現実的に難しいことが多いです。そのため,バイアスポテンシャルを課すことでMD計算中の遷移を早めることを考えます。
バイアスポテンシャルを課す対象を反応座標$${\hat{\lambda}(\mathbf{R})}$$そのものにしても良いのですが,ここではそれ以外の集団座標$${\hat{\mathbf{s}}(\mathbf{R})}$$に対してバイアスポテンシャルを設定することにします。$${\hat{\mathbf{s}}(\mathbf{R})}$$についても状態$${A, B}$$の違いを特徴づけられると仮定します。また,バイアスポテンシャルは$${\hat{\lambda}(\mathbf{R})=\lambda^*}$$において$${0}$$となる($${G(\lambda^*)}$$の値は変化しない)ように設定できると仮定します。
バイアスポテンシャルを$${V(\hat{\mathbf{s}}(\mathbf{R}))}$$とすると,早められた遷移時間$${\tau_{\rm M}}$$は(7)式となります。
$$
\begin{align*}
\tau_{\rm M}&=\frac{1}{\omega\kappa} \frac{\int_{\lambda\le\lambda^*}{\rm d}\lambda\int{\rm d}\mathbf{R}\delta\left(\hat{\lambda}(\mathbf{R})-\lambda\right)\exp\left(-\beta (U(\mathbf{R})+V(\hat{\mathbf{s}}(\mathbf{R})))\right)}{\int{\rm d}\mathbf{R}\delta\left(\hat{\lambda}(\mathbf{R})-\lambda^*\right)\exp\left(-\beta U(\mathbf{R})\right)}
\end{align*}\tag{7}
$$
$${\tau}$$と$${\tau_{\rm M}}$$は$${G(\lambda^*)}$$の寄与に関する部分が共通するため,比率を取ると$${G(\lambda^*)}$$の項をキャンセルアウトすることができます。
$$
\begin{align*}
\alpha &:=\frac{\tau}{\tau_{\rm M}}\\
&=\frac{\int_{\lambda\le\lambda^*}{\rm d}\lambda\int{\rm d}\mathbf{R}\delta\left(\hat{\lambda}(\mathbf{R})-\lambda\right)\exp\left(-\beta U(\mathbf{R})\right)}{\int_{\lambda\le\lambda^*}{\rm d}\lambda\int{\rm d}\mathbf{R}\delta\left(\hat{\lambda}(\mathbf{R})-\lambda\right)\exp\left(-\beta (U(\mathbf{R})+V(\hat{\mathbf{s}}(\mathbf{R})))\right)}\\
&=: \left\lang\exp\left(\beta V(\hat{\mathbf{s}}(\mathbf{R}))\right)\right\rang_{V, A}
\end{align*}\tag{8}
$$
ここで,$${\left\lang\cdots\right\rang_{V, A}}$$は,バイアスポテンシャル下における状態$${A}$$のみのアンサンブル平均を表します。
状態$${A}$$のみに限定されているため,エルゴード性の問題を気にすることなくアンサンブル平均を時間平均で評価できます。
バイアスポテンシャル下で$${\Delta t}$$毎に$${N}$$回サンプリングを実施した場合,$${\alpha}$$を
$$
\begin{align*}
\alpha &=\frac{1}{N}\sum_{i=1}^N\exp\left(\beta V(\hat{\mathbf{s}}(\mathbf{R}(i\Delta t)))\right)
\end{align*}\tag{9}
$$
から評価できます。
バイアスポテンシャル下でシミュレーションを行った際,$${t_b=N_b\Delta t}$$後に最初の遷移が発生したとすると,
$$
\begin{align*}
t &=\left[\frac{1}{N_b}\sum_{i=1}^{N_b}\exp\left(\beta V(\hat{\mathbf{s}}(\mathbf{R}(i\Delta t)))\right)\right]\times t_b\\
&=\left[\frac{1}{N_b}\sum_{i=1}^{N_b}\exp\left(\beta V(\hat{\mathbf{s}}(\mathbf{R}(i\Delta t)))\right)\right]\times N_b\Delta t\\
&=\sum_{i=1}^{N_b}\exp\left(\beta V(\hat{\mathbf{s}}(\mathbf{R}(i\Delta t)))\right)\Delta t
\end{align*}\tag{10}
$$
を用いて実際の遷移時間に変換できます。
$${\tau}$$は平均遷移時間なので,複数のシミュレーションを繰り返して$${t}$$に関する平均を取ることで得られます。
(10)式はサンプリング毎の経過時間を$${\Delta t\rightarrow \exp\left(\beta V(\hat{\mathbf{s}}(\mathbf{R}(i\Delta t)))\right)\Delta t}$$に変換した値を足し合わせることで実際の遷移時間に変換できると解釈できます。
Metadynamicsを採用する利点
前節の議論は$${\hat{\lambda}(\mathbf{R})=\lambda^*}$$においてバイアスポテンシャルが$${0}$$となるという条件の下に成立します。原理的にはバイアスポテンシャルはMetadynamicsでなくても成立しますが,反応座標における自由エネルギー地形を事前に把握できないことを考えると,アンブレラサンプリング等の事前に平衡点を定義しなければいけない手法は現実的に適用が難しいという問題に直面します。
その点,Metadynamicsはon-the-flyでバイアスポテンシャルを更新していきますので,その困難を回避しやすいという特長があります。具体的には$${\hat{\lambda}(\mathbf{R})=\lambda^*}$$にいる瞬間にバイアスポテンシャルを更新しなければよいということになりますが,$${\hat{\lambda}(\mathbf{R})=\lambda^*}$$周辺にいる滞在時間は非常に短いことを考えると,高頻度にバイアスポテンシャルを更新さえしなければ容易に条件を満たせそうです。これが「Infrequent」が必要条件となる背景の一つです。
一方,(10)式を用いた変換には注意が必要となる側面があります。バイアスポテンシャルが時間変化しているため,アンサンブル平均を時間平均に置き換えて良いかは,たとえサンプリング領域が状態$${A}$$に限定されていたとしても自明とは言えません。バイアスポテンシャルの更新間隔も$${\Delta t}$$であったとすると,$${\Delta t}$$間はバイアスポテンシャルは時間変化しないため,$${\Delta t}$$間に以下の条件を満たしていれば(10)式と同様の変換式を適用することができます。
バイアスポテンシャルを更新した影響が($${\Delta t}$$と比較して)速やかに平衡化
$${\Delta t}$$間に状態$${A}$$に対するアンサンブル平均と時間平均が一致する程度にサンプリングを行える
上記2条件は$${\Delta t}$$が長くなるほど成立しやすくなります。つまり,ここでも「Infrequent」が要求されるわけです。
以上の条件が満たされる$${\Delta t}$$でMetadynamicsを実行した場合,Metadynamicsでの遷移時間$${t_b}$$は(11)式を用いて実際の遷移時間$${t}$$に変換できます。
$$
\begin{align*}
t &=\sum_{i=1}^{N_b}\exp\left(\beta V(\hat{\mathbf{s}}(\mathbf{R}(i\Delta t),i\Delta t))\right)\Delta t
\end{align*}\tag{11}
$$
まとめ
通常のMD計算で平均遷移時間を見積もるのは困難なので,バイアスポテンシャルで遷移を早めることが望まれる
バイアスポテンシャルの影響を取り除く変換式は,自由エネルギー地形の極大値がバイアスポテンシャル有無で変化していない必要がある
自由エネルギー地形は事前に分かっていなくとも,on-the-flyでバイアスポテンシャルを更新していくMetadynamicsは必要条件を満たせる可能性が高い
自由エネルギー地形の極大値を変化させない,及びアンサンブル平均を時間平均に置き換えるために「Infrequent」なバイアスポテンシャルの更新が要求される
