軌道アンサンブル平均からのクルックスの揺動定理の導出
生体分子シミュレーションの主題の1つとして高精度な自由エネルギー計算が挙げられます。分子シミュレーションによる自由エネルギー計算は,2つの要素「サンプリング手法」及び「サンプリングデータからの自由エネルギー値の予測」から構成されます。この「サンプリングデータからの自由エネルギー値の予測」する手法の1つであるベネット受容比法(Bennett acceptance ratio method)は多くの市民権を得ているという印象がありますが,ベネット受容比法はクルックスの揺動定理と最尤法を用いると簡潔にかつ見通し良く導出することができます(参考文献1)。クルックスの揺動定理の表現は複数あるかと思いますが,参考文献1に倣うと以下のようになります。

P_{A→B}(W)はA→Bを生じるために必要となる仕事量がWとなる確率です。この式をエントロピー生成に置き換えた場合の解説動画が分かりやすいと思ったので,リンクしておきます。
クルックスの揺動定理は非平衡MDから自由エネルギーを求める際に使用されるジャルジンスキー等式を包含する形となっており,クルックスの揺動定理は分子シミュレーションによる自由エネルギー計算の世界において最も重要な定理の一つなのではないかと思います。参考文献2によると,クルックスの揺動定理は更に一般化された軌道アンサンブル平均を用いた定理から導出できることが示されています。そこで本記事では,軌道アンサンブル平均からクルックスの揺動定理の導出を数式の取り扱いに着目しながら説明します。また,系は粒子数N及び体積Vが一定で,内部エネルギーUをもち,熱浴Tに接している(平衡状態ではNVTアンサンブルとなる)と仮定します。
軌道アンサンブル平均とは?
軌道アンサンブル平均は,A → Bの変化を表した軌道(trajectory)がある確率で生じるものとみなし,軌道に関して統計平均を求めることを意味します。参考文献2によると,平衡状態にある熱力学的状態Aを熱力学的状態Bに変化させるために系に与えた仕事W(準静的である必要はありません)とAB間の自由エネルギー差の関係は,以下の軌道アンサンブル平均による関係式で与えられます。

ここで,FはA → Bの変化における系の配置の軌道を変関数とした汎関数,βは逆温度(1/T,ボルツマン定数を1とする単位系を採用),W_{d}は系に与えられた仕事Wと可逆仕事(=自由エネルギー差)の差分(W_{d} = W - ΔF_{AB})になります。Fにハットを付けたものは逆過程(B → Aの変化)を意味します。
Fの具体的な表式は例えば以下のような感じです(あくまで例ですので,以下のような表式に限定されるわけではありません)。

Fに関して軌道のアンサンブルでの平均を取るということは,ありうるすべての軌道に関して確率による重みづけ平均を取ることを意味します。確率の要素は初期状態Aの存在確率ρ,及びA → Bに特定の軌道を通じて遷移する確率Pの2つがあります。

軌道アンサンブル平均による関係式はとてもシンプルな形で表現されているものの,具体的な系に当てはめると複雑な数式になります。
参考文献2では軌道アンサンブル平均による関係式からいろいろな非平衡統計力学で知られた関係式を導出できることが示されています。本記事では,クルックスの揺動定理の導出に焦点を絞ります。
クルックスの揺動定理の導出
汎関数Fが

の場合,軌道アンサンブル平均による関係式に代入すると

となります。左辺はA → Bのすべての軌道の中から仕事がW( = W_d+ΔF_{AB})となるもののみを集約したことを意味するので,

と表現することにします。以上より,

となり,目的の表式と得ることができました。
エントロピー生成に関する表式
ΔF_{AB}はA → Bがどのような過程を経るかに依存せずに決まる量であり,Wとなる確率はW_dとなる確率に等しいです。クルックスの式をβW_dの確率で表現すると
![]()
となります。
ここで,系と熱浴のそれぞれのエントロピー変化を考えます。
A → Bにおいて熱浴から系に熱量Qが与えられたとすると,熱浴のエントロピー変化は
![]()
となります。
一方,系のエントロピー変化は
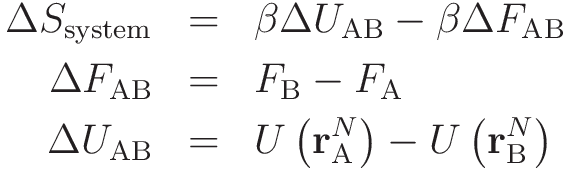
となります。また,内部エネルギーの変化は系に与えられた仕事Wと熱浴からの熱量Qによるものなので,
![]()
となります。以上をまとめて全体のエントロピー変化を計算すると

となります。これより,
![]()
が得られます。
ジャルジンスキー等式
積分しやすいよう
![]()
と式変形します。両辺をWに関して積分すると,

となり,ジャルジンスキー等式

が得られます。
参考文献
1. Phys. Rev. Lett. 91, 140601 (2003)
2. Phys. Rev. E 61, 2361 (1999)
3. ゆらぎの定理@東京理科大学
