Umbrella SamplingとWeighted Histogram Analysis Method

Umbrella Samplingは，反応座標のある点にピン止めされるようなポテンシャル（umbrella potential）を反応座標軸に沿って複数用意し，反応座標軸周辺を重点的にサンプリングする手法です。Umbrella Samplingで得られたサンプリングデータはUmbrella Potential込みの状態ですが，興味があるのはUmbrella Potentialがない状態での自由エネルギー形状（反応座標の確率分布）です。Umbrella Samplingで得られたサンプリングデータをUmbrella Potentialがない状態の情報に変換する手法の一つにWeighted Histogram Analysis Method（WHAM法）があります。この記事では，Umbrella SamplingとWHAM法を簡単に説明します。

Umbrella Potentialが有る無しでの確率分布

系のPotential energyをV(q)，Umbrella Potentialをw(s(q))（複数あるUmbrella Potential），反応座標をs(q)とおくと，反応座標点s(q) = xの存在確率は以下の様になります。
Umbrella Potentialがある場合：

Umbrella Potentialがない場合：

ここでβは逆温度を表します。
P_b(x)を式変形することでP(x)を用いた形で表現できます。

Umbrella Potentialは反応座標軸に沿って複数設けられるので，そのindexをθとすることにします。

Umbrella Potentialは調和型ポテンシャルが採用されることが多いです。

WHAM法

各Umbrella Potentialでの反応座標の確率分布を足し合わせると以下の様にり，これがWHAM法の出発点となる式となります。

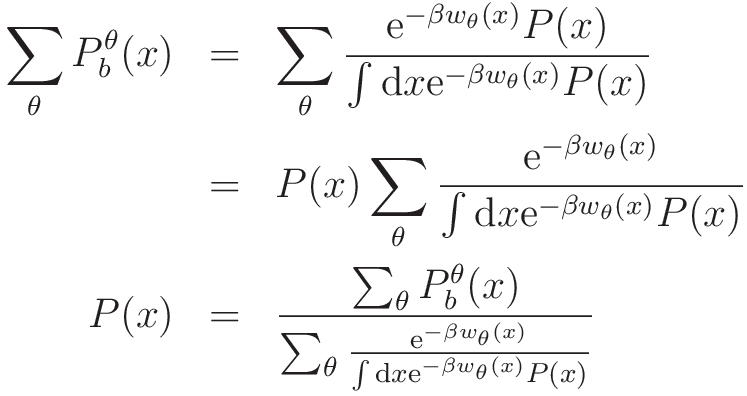
Umbrella Samplingで得られたHistogram（分子）がRe-weightされる（分母）されることで目的の確率分布が得られる表式になっています。

Umbrella Potential有の確率分布の推定

上記で得られたP(x)の表式を計算するためには，各Umbrella PotentialでのP_b^θ(x)の情報が必要です。P_b^θ(x)はUmbrella Samplingの結果から以下の値を代用することにします。

N_θはindex θのUmbrella Potentialにおける全サンプリングデータ数，n_θ(x)はs(q)=xとなったサンプリングデータ数です。

Umbrella Potentialなしの確率分布の推定

P(x)の表式は自分自身も含んだ形となっているため，P(x)に対してself-consistentな解を得る必要があります。WHAM法ではP(x)の適当な初期値を用意し，self-consistentな解が得られるまでiterativeにP(x)を更新します。以下の定義式

を用いて，より具体的な手順を説明します。

1. P_{θ,i}を計算
2. a_iを計算
3. c_{θ,i}を計算
4. P_iの初期値を適用に用意
5. d_{θ,i}を計算
6. a_i, c_{θ,i}, d_{θ,i}を用いてP_iを更新
7. P_iの値が収束するまで手順5～7を繰り返す