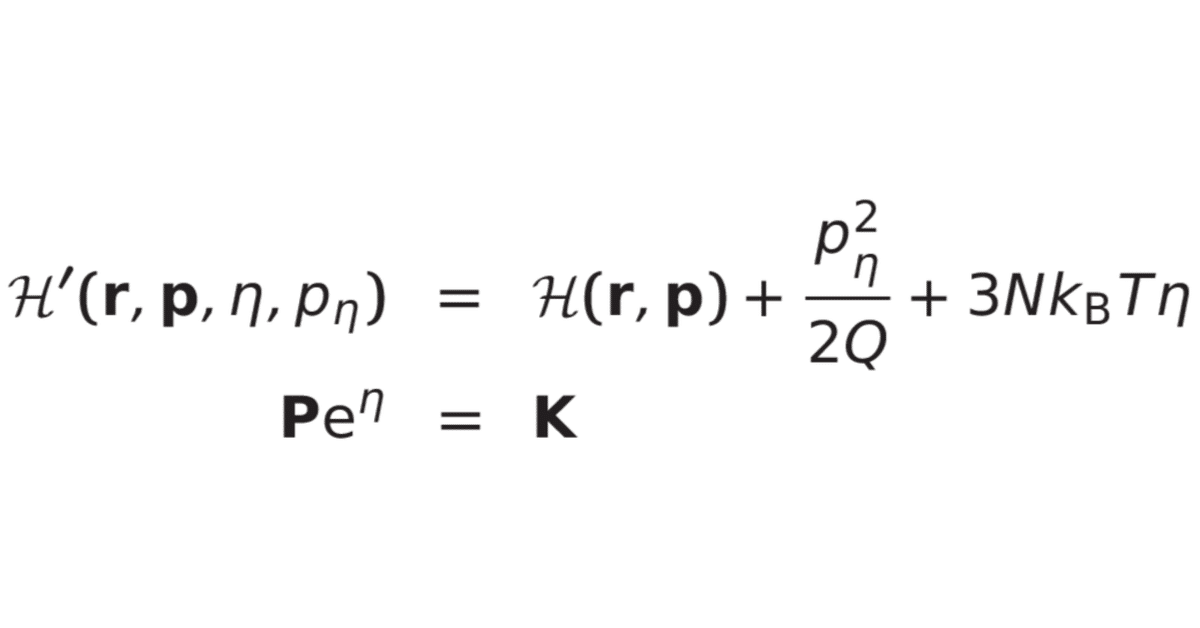
外力がない場合の能勢・フーバー熱浴の問題点
能勢・フーバー熱浴は,力学変数を拡張することによってNVTアンサンブルを実現する分子動力学シミュレーションの手法です。
本記事では,能勢・フーバー熱浴の解説するとともに,外力がない場合においてはNVTアンサンブルが実現されない問題が生じることを示します。
能勢・フーバー熱浴とは
物理的な系として,3次元空間の体積$${V}$$の箱の中に$${N}$$つの粒子が存在する状況を考えます。また,各粒子に働く力はポテンシャル$${U(\mathbf{r}_1,\cdots,\mathbf{r}_N)}$$で与えられるとします。
$${i}$$番目の粒子の質量を$${m_i}$$,運動量を$${\mathbf{p}_i}$$とすると,系のハミルトニアンは以下のようになります。
$$
\begin{align*}
\mathcal{H}(\mathbf{r},\mathbf{p})&=\sum_{i=1}^N\frac{\mathbf{p}_i^2}{2m_i}+U(\mathbf{r}_1,\cdots,\mathbf{r}_N)
\end{align*}\tag{1}
$$
実現したいのは,この物理系に対してNVTアンサンブルを得ることです。
そのため,力学変数$${\eta}$$,及びその共役運動量$${p_{\eta}}$$を追加し,トータルの力学系($${\{(\mathbf{r}_i,\mathbf{p}_i)\}+(\eta,p_{\eta})}$$)に対してNVEアンサンブル的な状態を生成することにより,興味ある物理系($${\{(\mathbf{r}_i,\mathbf{p}_i)\}}$$)に対してはNVTアンサンブルが生成されるような運動方程式を考えます。
天下り的ですが,能勢・フーバーの運動方程式は以下のようになります。
$$
\begin{align*}
\dot{\mathbf{r}}_i&:=\frac{{\rm d}\mathbf{r}_i}{{\rm d}t}\\
&=\frac{\mathbf{p}_i}{m_i}\\
\dot{\mathbf{p}}_i&=\mathbf{F}_i-\frac{p_{\eta}}{Q}\mathbf{p}_i\ \ \ \left(\mathbf{F}_i=-\frac{\partial U}{\partial \mathbf{r}_i}\right)\\
\dot{\eta}&=\frac{p_{\eta}}{Q}\\
\dot{p}_{\eta}&=\sum_{i=1}^N\frac{\mathbf{p}_i^2}{m_i}-3Nk_{\rm B}T\\
\end{align*}\tag{2}
$$
ここで,$${Q}$$は温度制御の強さに関わるパラメータ,$${k_{\rm B}}$$はボルツマン定数,$${T}$$は絶対温度です。
ハミルトニアン系ではないという話
位相空間ベクトル$${\mathbf{x}}$$とおくと,ハミルトン系には
$$
\begin{align*}
\nabla_{\mathbf{x}}\cdot\dot{\mathbf{x}}&=0
\end{align*}\tag{3}
$$
つまり,時間微分の発散が0になるという性質があります。
能勢・フーバーの運動方程式で扱う位相空間ベクトル$${\mathbf{x}=\begin{bmatrix}\mathbf{r}_1^{\rm T}&\cdots&\mathbf{r}_N^{\rm T}&\mathbf{P}_1^{\rm T}&\cdots&\mathbf{P}_N^{\rm T}&\eta&p_{\eta}\end{bmatrix}^{\rm T}}$$に対して式(3)の発散を計算してみると,
$$
\begin{align*}
\nabla_{\mathbf{x}}\cdot\dot{\mathbf{x}}&=\sum_{i=1}^N\frac{\partial \dot{\mathbf{r}}_i}{\partial \mathbf{r}_i}+\sum_{i=1}^N\frac{\partial \dot{\mathbf{p}}_i}{\partial \mathbf{p}_i}+\frac{\partial \dot{\eta}}{\partial \eta}+\frac{\partial \dot{p}_{\eta}}{\partial p_{\eta}}\\
&=-3N\frac{p_{\eta}}{Q}\\
&=-3N\dot{\eta}\\
&\neq 0
\end{align*}\tag{4}
$$
となり,能勢・フーバーの運動方程式はハミルトン系ではないということになります。
ハミルトン系ではない場合,位相空間上での積分する際に注意が必要となります。
ハミルトン系の場合,初期位置$${\mathbf{x}_0}$$周辺の微小体積要素$${{\rm d}\mathbf{x}_0}$$と$${t}$$時間後の位置$${\mathbf{x}_t}$$周辺の微小体積要素$${{\rm d}\mathbf{x}_t}$$には
$$
\begin{align*}
{\rm d}\mathbf{x}_0&={\rm d}\mathbf{x}_t
\end{align*}\tag{5}
$$
が成立しますが,ハミルトン系ではない場合には$${{\rm d}\mathbf{x}_0\neq{\rm d}\mathbf{x}_t}$$となります。
その代わりとして,ハミルトン系ではない場合には微小体積要素に以下の性質があることが知られています。
$$
\begin{align*}
{\rm e}^{-w(\mathbf{x}_0,0)}{\rm d}\mathbf{x}_0&={\rm e}^{-w(\mathbf{x}_t,t)}{\rm d}\mathbf{x}_t\\
\frac{{\rm d}w(\mathbf{x}_t,t)}{{\rm d}t}&:=\nabla_{\mathbf{x}}\cdot\dot{\mathbf{x}}
\end{align*}\tag{6}
$$
能勢・フーバーの場合は,$${{\rm e}^{-w(\mathbf{x}_t,t)}={\rm e}^{-3N\eta}}$$となります。
保存量について
前節でみたように能勢・フーバーはハミルトン系ではないのですが,以下のハミルトニアン様な量が保存する性質があり,能勢・フーバーハミルトニアンと称されたりします。
$$
\begin{align*}
\mathcal{H}'(\mathbf{r},\mathbf{p},\eta,p_{\eta})&=\mathcal{H}(\mathbf{r},\mathbf{p})+\frac{p_{\eta}^2}{2Q}+3Nk_{\rm B}T\eta
\end{align*}\tag{7}
$$
実際に時間微分してみると,
$$
\begin{align*}
\dot{\mathcal{H}}'(\mathbf{r},\mathbf{p},\eta,p_{\eta})&=\sum_{i=1}^N\frac{\mathbf{p}_i\cdot\dot{\mathbf{p}}_i}{m_i}+\sum_{i=1}^N\frac{\partial U}{\partial \mathbf{r}_i}\cdot\dot{\mathbf{r}}_i+\frac{p_{\eta}\dot{p}_{\eta}}{Q}+3Nk_{\rm B}T\dot{\eta}\\
&=\sum_{i=1}^N\frac{\mathbf{p}_i\cdot\left(\mathbf{F}_i-\frac{p_{\eta}}{Q}\mathbf{p}_i\right)}{m_i}-\sum_{i=1}^N\mathbf{F}_i\cdot\frac{\mathbf{p}_i}{m_i}\\
&\ \ \ \ +\frac{p_{\eta}\left(\sum_{i=1}^N\frac{\mathbf{p}_i^2}{m_i}-3Nk_{\rm B}T\right)}{Q}+3Nk_{\rm B}T\frac{p_{\eta}}{Q}\\
&=0
\end{align*}\tag{8}
$$
外力がない場合,$${\sum_{i=1}^N\mathbf{F}_i=\mathbf{0}}$$となりますが,この場合には重心運動量$${\mathbf{P}=\sum_{i=1}^N\mathbf{p}_i}$$に関して
$$
\begin{align*}
\mathbf{P}{\rm e}^{\eta}&=\mathbf{K}
\end{align*}\tag{9}
$$
も保存します。ここで,$${\mathbf{K}}$$は時間に依存しない定数です。
$${\sum_{i=1}^N\mathbf{F}_i=\mathbf{0}}$$の条件の下,式(9)を時間微分すると,
$$
\begin{align*}
\frac{{\rm d}}{{\rm d}t}\mathbf{P}{\rm e}^{\eta}&=\left\{\sum_{i=1}^N\left(\dot{\mathbf{p}}_i+\dot{\eta}\mathbf{p}_i\right)\right\}{\rm e}^{\eta}\\
&=\left\{\sum_{i=1}^N\left(\mathbf{F}_i-\frac{p_{\eta}}{Q}\mathbf{p}_i+\frac{p_{\eta}}{Q}\mathbf{p}_i\right)\right\}{\rm e}^{\eta}\\
&={\rm e}^{\eta}\sum_{i=1}^N\mathbf{F}_i\\
&=\mathbf{0}
\end{align*}\tag{10}
$$
となります。
保存量が1つしかない場合の分配関数
$${\mathbf{x}}$$が運動方程式にしたがって時間発展させた場合,保存則を満たす領域内で軌跡が生成されます。
そのため,式(7)の保存量のみがある場合の分配関数$${\mathcal{Z}}$$は,
$$
\begin{align*}
\mathcal{Z}&=\int{\rm d}\mathbf{x}{\rm e}^{-3N\eta}\delta\left(\mathcal{H}(\mathbf{r},\mathbf{p})+\frac{p_{\eta}^2}{2Q}+3Nk_{\rm B}T\eta-\mathcal{H}'\right)
\end{align*}\tag{11}
$$
となります。
式(11)を拡張変数について積分すると,
$$
\begin{align*}
\mathcal{Z}&=\int{\rm d}^N\mathbf{r}\int{\rm d}^N\mathbf{p}\int{\rm d}p_{\eta}\int{\rm d}\eta{\rm e}^{-3N\eta}\delta\left(\mathcal{H}(\mathbf{r},\mathbf{p})+\frac{p_{\eta}^2}{2Q}+3Nk_{\rm B}T\eta-\mathcal{H}'\right)\\
&=\int{\rm d}^N\mathbf{r}\int{\rm d}^N\mathbf{p}\int{\rm d}p_{\eta}{\rm e}^{-\frac{\mathcal{H}(\mathbf{r},\mathbf{p})+\frac{p_{\eta}^2}{2Q}}{k_{\rm B}T}}\\
&=\left(\int{\rm d}p_{\eta}{\rm e}^{-\frac{p_{\eta}^2}{2Qk_{\rm B}T}}\right)\int{\rm d}^N\mathbf{p}\mathbf{r}\int{\rm d}^N{\rm e}^{-\frac{\mathcal{H}(\mathbf{r},\mathbf{p})}{k_{\rm B}T}}\\
&\propto\int{\rm d}^N\mathbf{r}\int{\rm d}^N\mathbf{p}{\rm e}^{-\frac{\mathcal{H}(\mathbf{r},\mathbf{p})}{k_{\rm B}T}}
\end{align*}\tag{12}
$$
となり,物理系に対してはカノニカル分布となることが示されます。
保存量が2つある場合の分配関数
一方,式(9)の保存量もある場合の分配関数$${\mathcal{Z}}$$は,
$$
\begin{align*}
\mathcal{Z}&=\int{\rm d}\mathbf{x}{\rm e}^{-3N\eta}\delta\left(\mathcal{H}(\mathbf{r},\mathbf{p})+\frac{p_{\eta}^2}{2Q}+3Nk_{\rm B}T\eta-\mathcal{H}'\right)\delta\left(\mathbf{P}{\rm e}^{\eta}-\mathbf{K}\right)
\end{align*}\tag{13}
$$
となり,$${\delta\left(\mathbf{P}{\rm e}^{\eta}-\mathbf{K}\right)}$$があるため,$${\eta}$$について簡単に積分することができません。
ここで,以下の変数変換を考えます。
$$
\begin{align*}
\mathbf{R}&:=\frac{\sum_{i=1}^Nm_i\mathbf{r}_i}{\sum_{i=1}^Nm_i}\\
&=:\frac{\sum_{i=1}^Nm_i\mathbf{r}_i}{M}\\
\mathbf{r}_k'&:=\mathbf{r}_k-\frac{\sum_{l=1}^Nm_i\mathbf{r}_i}{\sum_{l=1}^{k-1}m_l}\ \ \ \ {\rm for}\ k=2,\cdots,N\\
&=:\mathbf{r}_k-\frac{\sum_{l=1}^Nm_i\mathbf{r}_i}{m_k'}\\
\end{align*}\tag{13}
$$
この変数変換に対して,運動エネルギーは
$$
\begin{align*}
\sum_{i=1}^N\frac{m_i}{2}\mathbf{r}_i^2&=\frac{M}{2}\mathbf{R}^2+\sum_{i=2}^N\frac{1}{2}\frac{m_{i-1}'m_i}{m_i'}(\mathbf{r}_i')^2\\
&=:\frac{M}{2}\mathbf{R}^2+\sum_{i=2}^N\frac{\mu_i}{2}(\mathbf{r}_i')^2\\
\end{align*}\tag{14}
$$
となります。
また,正準共役な運動量は,
$$
\begin{align*}
\mathbf{P}&:=M\dot{\mathbf{R}}\\
\mathbf{p}_k'&:=\mu_k\dot{\mathbf{r}}_k'\ \ \ \ {\rm for}\ k=2,\cdots,N\\
\end{align*}\tag{15}
$$
となります。
つまり,変数変換後の物理的なハミルトニアン$${\tilde{\mathcal{H}}(\mathbf{R},\mathbf{P},\mathbf{r}',\mathbf{p}')}$$を
$$
\begin{align*}
\tilde{\mathcal{H}}(\mathbf{R},\mathbf{P},\mathbf{r}',\mathbf{p}')&=\frac{1}{2M}\mathbf{P}^2+\sum_{i=2}^N\frac{1}{2\mu_i}(\mathbf{p}_i')^2+\tilde{U}(\mathbf{r}_2',\cdots,\mathbf{r}_N')\\
&=:\frac{1}{2M}\mathbf{P}^2+\mathcal{H}(\mathbf{r}',\mathbf{p}')
\end{align*}\tag{16}
$$
と表すことができます。
これらを用いて,分配関数$${\mathcal{Z}}$$を計算すると,
$$
\begin{align*}
\mathcal{Z}&=\int{\rm d}^{N-1}\mathbf{r}'\int{\rm d}^{N-1}\mathbf{p}'\int{\rm d}\mathbf{R}\int{\rm d}\mathbf{P}\int{\rm d}\eta\int{\rm d}p_{\eta}{\rm e}^{-3N\eta}\delta\left(\frac{1}{2M}\mathbf{P}^2+\mathcal{H}(\mathbf{r}',\mathbf{p}')+\frac{p_{\eta}^2}{2Q}+3Nk_{\rm B}T\eta-\mathcal{H}'\right)\delta\left(\mathbf{P}{\rm e}^{\eta}-\mathbf{K}\right)\\
&=V\int{\rm d}^{N-1}\mathbf{r}'\int{\rm d}^{N-1}\mathbf{p}'\int{\rm d}\eta\int{\rm d}p_{\eta}{\rm e}^{-3(N-1)\eta}\delta\left(\mathcal{H}(\mathbf{r}',\mathbf{p}')+\frac{\mathbf{K}^2{\rm e}^{-2\eta}}{2M}+\frac{p_{\eta}^2}{2Q}+3Nk_{\rm B}T\eta-\mathcal{H}'\right)\\
\end{align*}
$$
となります。
デルタ関数の中に$${\frac{\mathbf{K}^2{\rm e}^{-2\eta}}{2M}}$$が含まれる関係で,物理系はカノニカル分布にならなそうです。本当なら$${\eta,p_{\eta}}$$について積分しないと証明したことにはなりませんが,$${\eta}$$と$${p_{\eta}}$$のどちらか片方のみでしたら積分できるのですが,両方の変数に関して積分の解析解を見出すことはできませんでした。。。(積分方法をご存じの方がいらっしゃいましたら教えてください<(_ _)>)
参考文献
Mark Tuckerman, Statistical Mechanics: Theory and Molecular Simulation (Oxford Graduate Texts)
