
Statistical Mechanics: Theory and Molecular Simulation Chapter 7 - Monte Carlo
Statistical Mechanics: Theory and Molecular SimulationはMark Tuckermanによって著された分子シミュレーションに関連した熱・統計物理学,及び量子力学の参考書になります。
現時点では(恐らく)和訳がないこともあり,日本での知名度はあまりないような気がしますが,被引用数が1400を超えていることを考えると海外では高く認知されている参考書みたいです。
https://scholar.google.com/citations?user=w_7furwAAAAJ&hl=ja
本記事では,Chapter 7(Monte Carlo)の章末問題の和訳とその解答例を紹介します。解答例に間違いが見受けられた場合はお知らせいただけると助かります。
Problem 7.1
以下の積分
$$
\begin{align*}
I&=\int_0^1{\rm d}{\rm e}^{-x^2}
\end{align*}
$$
を計算するためのモンテカルロプログラムを以下の場合に応じて書け。
a. $${[0,1]}$$の区間に対して$${x}$$を均一サンプリングする場合
b. 以下の重要度関数$${h(x)}$$を用いた場合
$$
\begin{align*}
h(x)&=\frac{3}{2}\left(1-x^2\right)
\end{align*}
$$
$${h(x)}$$は$${\exp(-x^2)}$$をテイラー展開した最初の2項で構成されている。
両方の場合において,モンテカルロ法で得られた結果をシンプソン法などを用いて単純に数値積分した場合の$${I}$$の値と比較せよ。
a. pythonによるコード例を以下に示す。
from matplotlib import pyplot as plt
from scipy import special
import numpy as np
# The number of sampling
n = 100000
# Analytical value
ana = special.erf(1) * np.sqrt(np.pi) * 0.5
# The below is the code
sampling = np.random.rand(n)
f = np.exp(-1 * sampling ** 2)
x = np.arange(5000, n + 1, 5000)
value = np.array([np.mean(f[:i]) for i in x ])
error = np.array([np.std(f[:i]) / np.sqrt(i) for i in x ])
fig, ax = plt.subplots()
ax.errorbar(x, value, yerr = error, capsize = 2, fmt = 'o', ecolor = 'red', color = 'black', label = 'numerical')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.axhline(ana, ls = "-.", color = "magenta", label = 'analytical')
ax.set_ylim(0.99 * ana, 1.01 * ana)
plt.legend()
plt.show()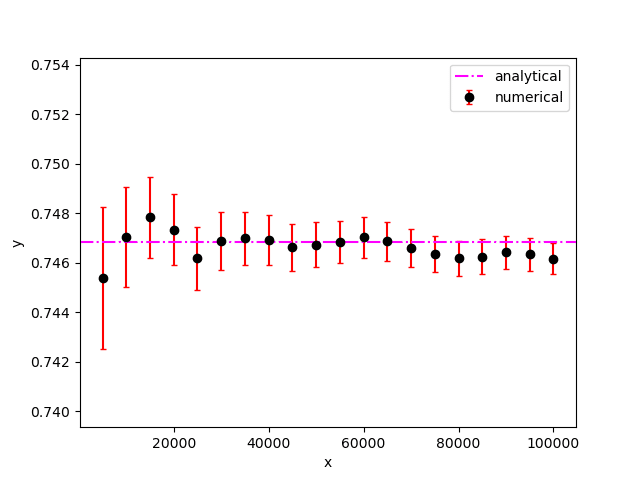
b. pythonによるコード例を以下に示す。
from matplotlib import pyplot as plt
from scipy import special
import numpy as np
import sympy
# The number of sampling
n = 1000
# Analytical value
ana = special.erf(1) * np.sqrt(np.pi) * 0.5
def generateSamples(n):
sampling = []
x = sympy.Symbol('x')
for _ in range(n):
a = np.random.rand()
Sol = [complex(s).real for s in sympy.solve(x ** 3 - 3 * x + 2 * a) ]
for s in Sol:
if 0 <= s <= 1:
sampling.append(s)
break
return np.array(sampling)
# The below is the code
sampling = generateSamples(n)
f = np.exp(-1 * sampling ** 2) /(1.5 * (1 - sampling ** 2))
x = np.arange(50, n + 1, 50)
value = np.array([np.mean(f[:i]) for i in x ])
error = np.array([np.std(f[:i]) / np.sqrt(i) for i in x ])
print(value[-1], error[-1])
fig, ax = plt.subplots()
ax.errorbar(x, value, yerr = error, capsize = 2, fmt = 'o', ecolor = 'red', color = 'black', label = 'numerical')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.axhline(ana, ls = "-.", color = "magenta", label = 'analytical')
#ax.set_ylim(0.99 * ana, 1.01 * ana)
plt.legend()
plt.show()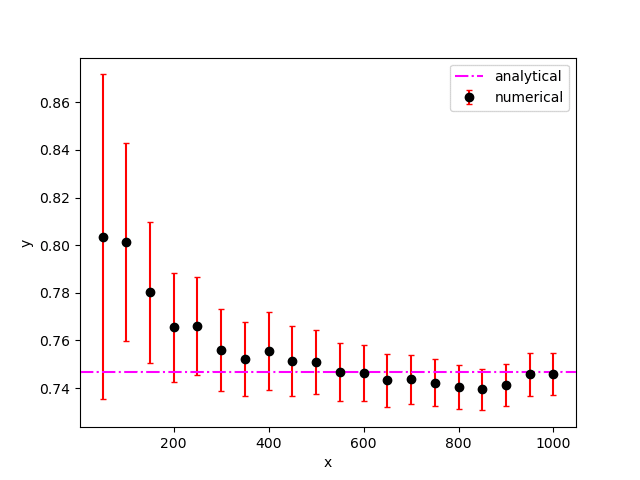
Problem 7.2
以下の積分に対する重要度関数を考案し,その重要度関数が均一サンプリングの場合よりも分散が小さいことを実証するモンテカルロプログラムを書け。重要度関数を用いた場合は$${I}$$の解析解との誤差が$${10^{-6}}$$以内に収束するために必要となるサンプリング数はどの程度になるであろうか?
$$
\begin{align*}
I&=\int_0^1{\rm d}x\cos\left(\frac{\pi x}{2}\right)
\end{align*}
$$
以下の重要度関数を考える。
$$
\begin{align*}
h(x) &=\begin{cases}-\frac{9}{7}x +\frac{12}{7}& 0 \leq x < \frac{2}{3}\\ -\frac{18}{7}x +\frac{18}{7}& \frac{2}{3} \leq x \leq 1\end{cases}
\end{align*}
$$
pythonによるコード例を以下に示す。
from matplotlib import pyplot as plt
import numpy as np
import sympy
np.random.seed(seed = 1)
# The number of sampling
n = 10000000
# Analytical value
I_a = 2 / np.pi
sum_u = 0.0
sum_i = 0.0
# The below is the code
sample_u = []
sample_i = []
for i in range(1, n + 1):
r = np.random.rand()
sum_u += np.cos(0.5 * np.pi * r)
if r < 6 / 7:
x = (4 - np.sqrt(16 - 14 * r)) / 3
else:
x = 1 - np.sqrt(1 - 7 * (r - 6 / 7) / 9)
if x < 2 / 3:
sum_i += np.cos(0.5 * np.pi * x) / (-9 * x + 12) * 7
else:
sum_i += np.cos(0.5 * np.pi * x) / (-18 * x + 18) * 7
sample_u.append(r)
sample_i.append(x)
I_u = sum_u / i
err_u = abs((I_u - I_a) / I_a)
I_i = sum_i / i
err_i = abs((I_i - I_a) / I_a)
#print(i, I_i, I_u, I_a,err_i, err_u)
if err_i < 1e-6:
break
sample_u = np.array(sample_u)
sample_i = np.array(sample_i)
plt.hist([sample_i, sample_u], stacked = False, label = ['important', 'uniform'])
plt.legend()
plt.show()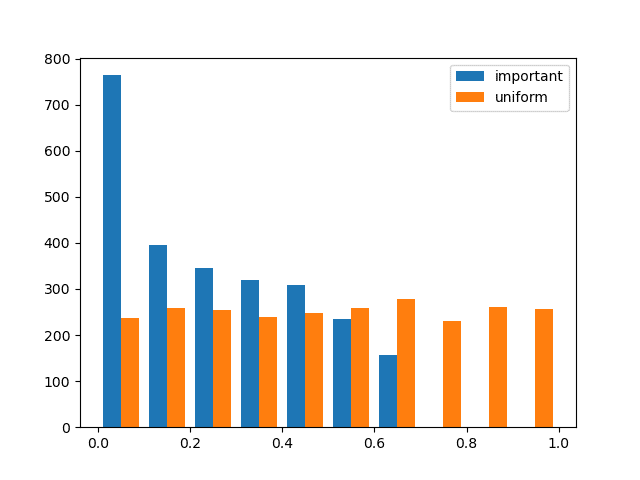
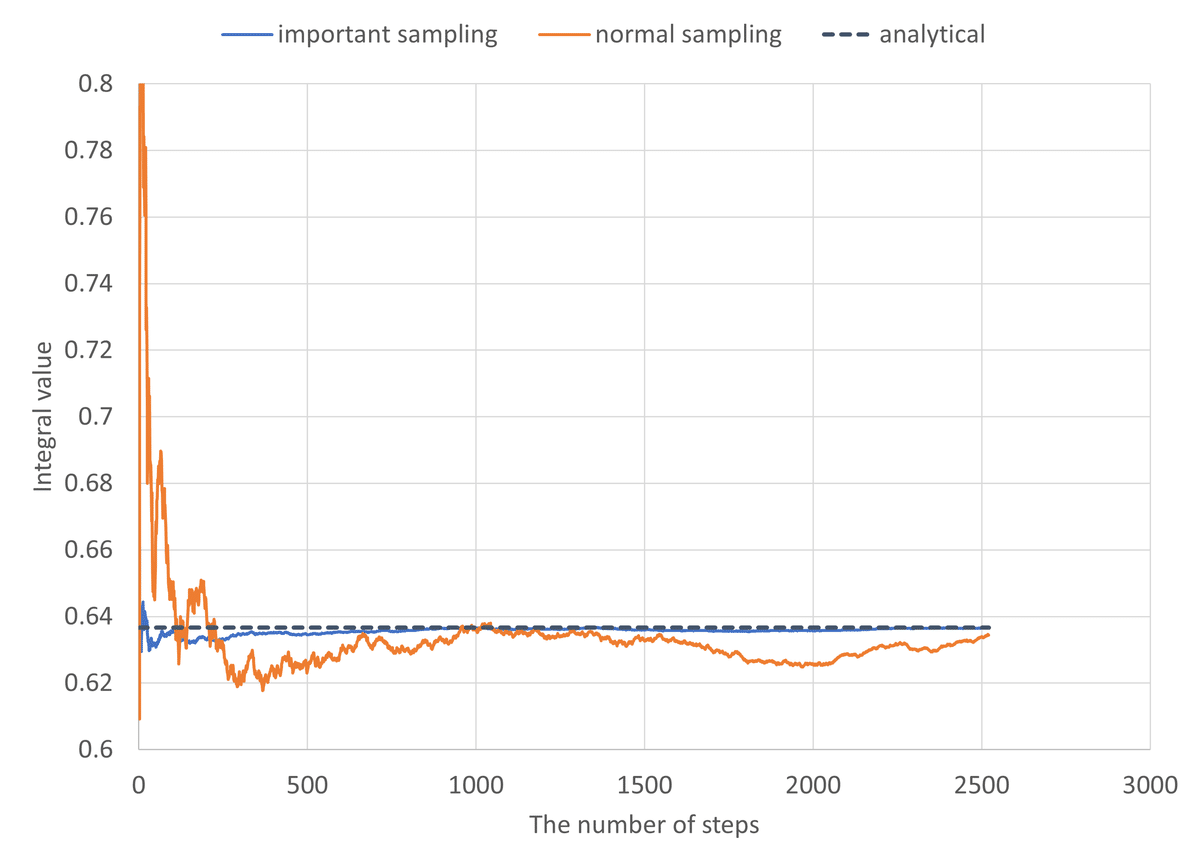
2,500回強で収束に至ったが,収束に必要なサンプリング数はシード値に著しく依存する性質が確認された。より細かく区分を区切った重要度関数を用いることにより,より早くかつより安定的に収束させることができることが期待される。
Problem 7.3
以下(Kalos and Whitlock, 1986)は$${\rm M(RT)^2}$$アルゴリズムに関する漸化式の一例である。一次元の確率分布$${f(x)=2x \ (x\in (0,1))}$$をサンプリングするための$${\rm M(RT)^2}$$アルゴリズムを考える。$${y}$$から$${x}$$への遷移確率が
$$
\begin{align*}
T(x|y) &=\begin{Bmatrix}1 & x\in (0,1)\\
0&{\rm otherwise}\end{Bmatrix}
\end{align*}
$$
で与えられるとする。
また,$${r(x|y)=x/y (\in (0,1))}$$であるとする。
a. 分布の数列$${\pi_n(x)}$$が以下の漸化式を満たすことを示せ。
$$
\begin{align*}
\pi_{n+1}(x) &=\int_x^1{\rm d}y\frac{x}{y}\pi_n(y)+\int_0^x{\rm d}y\pi_n(y)+\pi_n(x)\int_0^x{\rm d}y\left(1-\frac{y}{x}\right)
\end{align*}
$$
b. $${\pi_n(x)=cx}$$が不動点であることを示せ,ここで$${c}$$は任意の定数である。正規化の観点から$${c=2}$$であるべきである。
c. $${\pi_0(x)=3x^2}$$から漸化式を始めた場合,$${n}$$回の反復によって
$$
\begin{align*}
\pi_{n}(x) &=a_nx+c_nx^{n+2}
\end{align*}
$$
が得られる。$${n\rightarrow 0}$$のとき,$${c_n}$$が漸近的に$${0}$$に収束する,つまり分布が線形関数に収束することを示せ。
$${n+1}$$回目で$${x}$$にいるためには,
$${n}$$回目で$${x}$$にいて,遷移せずにとどまる
$${n}$$回目で$${y}$$にいて,$${x}$$に遷移する
の過程がある。
過程1の寄与は$${\pi_n(x)\int_0^x{\rm d}y\left(1-\frac{y}{x}\right)}$$と計算される。$${y>x}$$だと$${y}$$への遷移確率が$${1}$$となってしまうため,積分範囲は$${[0,x]}$$となる。
過程2の寄与は,$${x>y}$$において遷移確率が$${1}$$となることを考慮すると,$${\int_x^1{\rm d}y\frac{x}{y}\pi_n(y)+\int_0^x{\rm d}y\pi_n(y)}$$となる。
以上より,
$$
\begin{align*}
\pi_{n+1}(x) &=\int_x^1{\rm d}y\frac{x}{y}\pi_n(y)+\int_0^x{\rm d}y\pi_n(y)+\pi_n(x)\int_0^x{\rm d}y\left(1-\frac{y}{x}\right)
\end{align*}
$$
となる。
b. $${\pi_n(x)=cx}$$のとき,
$$
\begin{align*}
\pi_{n+1}(x) &=\int_x^1{\rm d}y\frac{x}{y}cy+\int_0^x{\rm d}ycy+cx\int_0^x{\rm d}y\left(1-\frac{y}{x}\right)\\
&=cx(1-x)+\frac{c}{2}x^2+cx\left(x-\frac{x}{2}\right)\\
&=cx=\pi_n(x)
\end{align*}
$$
となるため,$${\pi_n(x)=cx}$$は漸化式の不動点である。
c.$${n\geq2}$$において,
$$
\begin{align*}
a_n&=\frac{3}{2}+\sum_{l=3}^{n+1}\frac{1}{l}\\
c_n&=\prod_{m=2}^n\left(\frac{1}{2}-\frac{1}{m+1}+\frac{1}{m+2}\right)
\end{align*}
$$
となるため,$${n\rightarrow \infty}$$で$${c_n\rightarrow 0}$$に収束する。
Problem 7.4
この問題では,カノニカルアンサンブルに従う1次元の調和振動子系に対して,この章で紹介されたモンテカルロスキームの幾つかを熱浴を扱う分子動力学と比較することにする。
$$
\begin{align*}
U(x)&=\frac{1}{2}m\omega^2x^2
\end{align*}
$$
問題を扱う上で$${m=1, \omega=1}$$(ついでに$${\beta=1}$$)として差支えない。
a. $${\rm M(RT)^2}$$アルゴリズムを用いて$${x}$$を均一サンプリングすることにより,カノニカルアンサンブル平均$${\langle x^4\rangle}$$を計算するモンテカルロプログラムを書け。分散を限りなく小さくするためにステップサイズ$${\Delta}$$及び平均受理確率を最適化するよう試みよ。
b. $${x}$$の試行移動を生成するために速度ベルレ法を用いた混合モンテカルロプログラムを書き,a.と同様に$${\langle x^4\rangle}$$を計算せよ。分散を限りなく小さくするために時間ステップ及び平均受理確率を最適化するよう試みよ。
c. 式(4.11.8)-(4.11.17)で表されるNose-Hoover chain方程式を用いて熱浴と接した場合の分子動力学プログラムを書け。式(4.11.12)にある重み係数を用いて$${n_{\rm sy}=7}$$に設定し,また$${n=4}$$を用いよ。式(4.10.3)のエネルギーが式(3.14.1)で評価した場合に$${10^{-4}}$$のオーダーで保存するよう時間ステップを調整せよ。
d. $${\langle x\rangle^4}$$を収束(分散がある値以下に収束)させるために必要となるステップ数を各アルゴリズム間で比較せよ。この問題に対するモンテカルロと分子動力学の効率はどうなるであろうか?
a. pythonによる実装例を以下に示す。
from matplotlib import pyplot as plt
import numpy as np
np.random.seed(seed = 2023)
# Input parameters
Delta = 3.0 # Step size
x_i = 0.0 # initial position
I_a = 3 # Analytical value
err1 = 1e-2 # Convergence Criterion for difference from the analytical value
err2 = 1e-2 # Convergence Criterion for variance
def U(x):
return 0.5 * x ** 2
# The below is the code
x_now = x_i
sum_x4_n = 0.0
sum_x8_n = 0.0
err_n = 1
diff = 1
n_step = 1
A_list = []
I_n_list = []
err_n_list = []
n_step_list = []
accept = 0
while (diff > err1) or (err_n > err2):
x_c = x_now + (np.random.rand() - 0.5) * Delta
A = np.min([1, np.exp(-1 * (U(x_c) - U(x_now)))])
if A >= np.random.rand():
x_now = x_c
accept += 1
sum_x8_n += x_now ** 8
sum_x4_n += x_now ** 4
I_n = sum_x4_n / n_step
err_n = np.sqrt(sum_x8_n / n_step - I_n ** 2) / np.sqrt(n_step)
A_list.append(A)
diff = abs((I_a - I_n) / I_a)
if n_step % 10000 == 0:
print(n_step, x_now, I_n, err_n, diff)
I_n_list.append(I_n)
err_n_list.append(err_n)
n_step_list.append(n_step)
n_step += 1
print(f"The number of steps required for convergence:{n_step}")
print(f"Average acceptance probability:{accept / n_step}")
fig, ax = plt.subplots()
ax.errorbar(n_step_list, I_n_list, yerr = err_n_list, capsize = 1, fmt = 'o', ecolor = 'red', color = 'black', label = 'numerical')
ax.set_xlabel('The number of steps')
ax.set_ylabel('Integral value')
ax.axhline(I_a, ls = "-.", color = "magenta", label = 'analytical')
plt.legend()
plt.savefig("6.4_a.png") 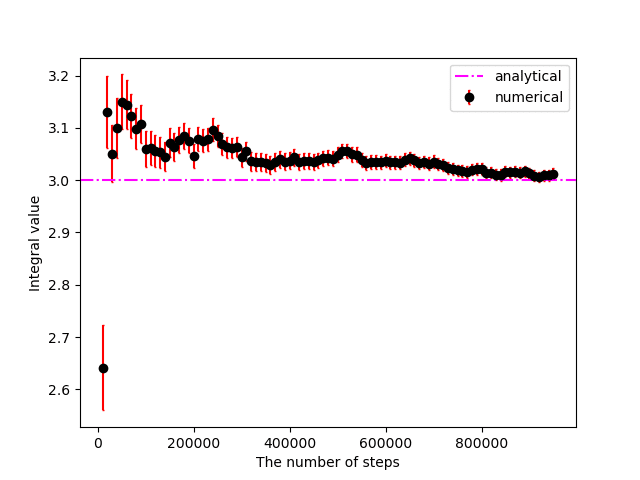
$${{\rm abs}((I_{\rm analytical} - I_{\rm numerical} )/I_{\rm analytical} ) \leq 0.01}$$かつ$${\delta \psi \leq 0.01}$$に収束するまでに956,907ステップを要した。
(収束はランダムシード値に著しく依存するため,あくまで参考値)
b. pythonによる実装例を以下に示す。
from matplotlib import pyplot as plt
import numpy as np
np.random.seed(seed = 2023)
# Input parameters
dt = 2.5 # Step size
x_i = 0.0 # Initial position
p_i = 1.0 # Initial momentum
I_a = 3 # Analytical value
err1 = 1e-2 # Convergence Criterion for difference from the analytical value
err2 = 1e-2 # Convergence Criterion for variance
def H(x, p):
return 0.5 * p ** 2 + 0.5 * x ** 2
def U(x):
return 0.5 * x ** 2
def F(x):
return -1 * x
# The below is the code
x_now = x_i
p_now = p_i
sum_x4_n = 0.0
sum_x8_n = 0.0
err_n = 1
diff = 1
n_step = 1
accept = 0
I_n_list = []
err_n_list = []
n_step_list = []
while (diff > err1) or (err_n > err2):
x_c = x_now
p_c = p_now
for _ in range(5):
p_c += 0.5 * dt * F(x_c)
x_c += dt * p_c
p_c += 0.5 * dt * F(x_c)
A = np.min([1, np.exp(-1 * (H(x_c, p_c) - H(x_now, p_now)))])
if A >= np.random.rand():
x_now = x_c
p_now = p_c
accept += 1
else:
p_now = np.random.normal(0, 1)
sum_x8_n += x_now ** 8
sum_x4_n += x_now ** 4
I_n = sum_x4_n / n_step
err_n = np.sqrt(sum_x8_n / n_step - I_n ** 2) / np.sqrt(n_step)
diff = abs((I_a - I_n) / I_a)
if n_step % 10000 == 0:
print(n_step, x_now, I_n, err_n, diff, accept / n_step)
I_n_list.append(I_n)
err_n_list.append(err_n)
n_step_list.append(n_step)
n_step += 1
print(f"The number of steps required for convergence:{n_step}")
print(f"Average acceptance probability:{accept / n_step}")
fig, ax = plt.subplots()
ax.errorbar(n_step_list, I_n_list, yerr = err_n_list, capsize = 1, fmt = 'o', ecolor = 'red', color = 'black', label = 'numerical')
ax.set_xlabel('The number of steps')
ax.set_ylabel('Integral value')
ax.axhline(I_a, ls = "-.", color = "magenta", label = 'analytical')
plt.legend()
plt.savefig("6.4_b.png") 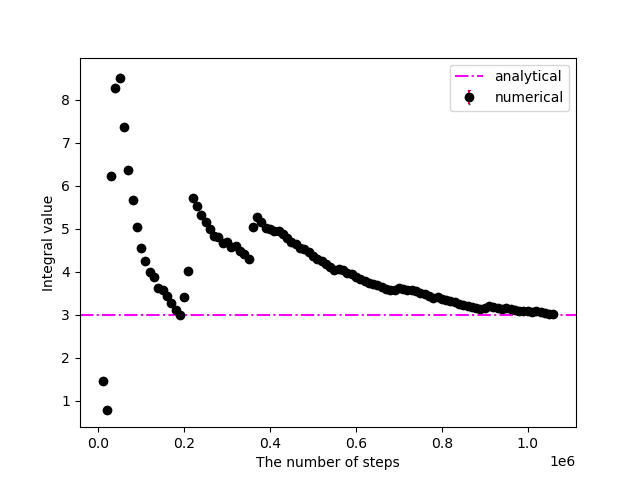
$${{\rm abs}((I_{\rm analytical} - I_{\rm numerical} )/I_{\rm analytical} ) \leq 0.01}$$かつ$${\delta \psi \leq 0.01}$$に収束するまでに1,042,846ステップを要した。
c. pythonによる実装例を以下に示す。
from matplotlib import pyplot as plt
import itertools
import numpy as np
np.random.seed(seed = 2023)
# Input parameters
N_c = 4 # The number of decompotiosion for the operator exp(i * L_NHC * dt / 2)
dt = 0.025 # time step size
M = 2 # The number of chains
Q = 1 # The time scale parameter for all chains
x_i = 0.0 # Initial position
p_i = np.random.normal(0, 1) # Initial momentum
eta = np.zeros(M)
p_eta = np.random.normal(0, 1, M)
I_a = 3 # Analytical value
err1 = 1e-2 # Convergence Criterion for difference from the analytical value
err2 = 1e-2 # Convergence Criterion for variance
# Seven weights of the Yodhida scheme for a sixth-order scheme
N_sy = 7
w = [0] * N_sy
w[0] = w[6] = 0.784513610477560
w[1] = w[5] = 0.235573213359357
w[2] = w[4] = -1.17767998417887
w[3] = 1 - 2 * np.sum(w[:3])
# Define functions
def updateDynamicalVariables(x_now, p_now, eta, p_eta):
for n_c, n_sy in itertools.product(range(N_c), range(N_sy)):
scale = 1.0
KE = p_now ** 2
delta_j = w[n_sy] * dt / N_c
p_eta[M - 1] += 0.25 * delta_j * (p_eta[M - 2] ** 2 / Q - 1)
for m in range(M - 2, -1, -1):
p_eta[m] *= np.exp(-0.125 * delta_j * p_eta[m + 1])
if m == 0:
p_eta[m] += 0.25 * delta_j * (KE - 1)
else:
p_eta[m] += 0.25 * delta_j * (p_eta[m - 1] ** 2 / Q - 1)
p_eta[m] *= np.exp(-0.125 * delta_j * p_eta[m + 1])
scale *= np.exp(-0.5 * delta_j * p_eta[0] / Q)
KE *= np.exp(-1.0 * delta_j * p_eta[0] / Q)
for m in range(M):
eta[m] += 0.5 * delta_j * p_eta[m]
for m in range(0, M - 1, 1):
p_eta[m] *= np.exp(-0.125 * delta_j * p_eta[m + 1])
G = KE - 1 if m == 0 else p_eta[m - 1] ** 2 / Q - 1
p_eta[m] += 0.25 * delta_j * G
p_eta[m] *= np.exp(-0.125 * delta_j * p_eta[m + 1])
p_eta[M - 1] += 0.25 * delta_j * (p_eta[M - 2] ** 2 / Q - 1)
p_now *= scale
return x_now, p_now, eta, p_eta
def conservedEnergy(x, p, eta, p_eta):
return 0.5 * p ** 2 + 0.5 * x ** 2 + 0.5 * np.sum(np.array(p_eta) ** 2) / Q + np.sum(eta)
# The below is the code
x_now = x_i
p_now = p_i
sum_x4_n = 0.0
sum_x8_n = 0.0
err_n = 1
dH = 0.0
diff = 1
n_step = 1
I_n_list = []
err_n_list = []
n_step_list = []
H0 = conservedEnergy(x_now, p_now, eta, p_eta)
while (diff > err1) or (err_n > err2):
x_now, p_now, eta, p_eta = updateDynamicalVariables(x_now, p_now, eta, p_eta)
p_now -= 0.5 * dt * x_now
x_now += dt * p_now
p_now -= 0.5 * dt * x_now
x_now, p_now, eta, p_eta = updateDynamicalVariables(x_now, p_now, eta, p_eta)
H = conservedEnergy(x_now, p_now, eta, p_eta)
dH += abs(H / H0 - 1)
err_H = dH / n_step
sum_x8_n += x_now ** 8
sum_x4_n += x_now ** 4
I_n = sum_x4_n / n_step
err_n = np.sqrt(sum_x8_n / n_step - I_n ** 2) / np.sqrt(n_step)
diff = abs((I_a - I_n) / I_a)
if n_step % 10000 == 0:
print(n_step, x_now, I_n, err_n, diff, err_H)
I_n_list.append(I_n)
err_n_list.append(err_n)
n_step_list.append(n_step)
n_step += 1
print(f"The number of steps required for convergence:{n_step}")
fig, ax = plt.subplots()
ax.errorbar(n_step_list, I_n_list, yerr = err_n_list, capsize = 1, fmt = 'o', ecolor = 'red', color = 'black', label = 'numerical')
ax.set_xlabel('The number of steps')
ax.set_ylabel('Integral value')
ax.axhline(I_a, ls = "-.", color = "magenta", label = 'analytical')
plt.legend()
plt.savefig("6.4_c.png") 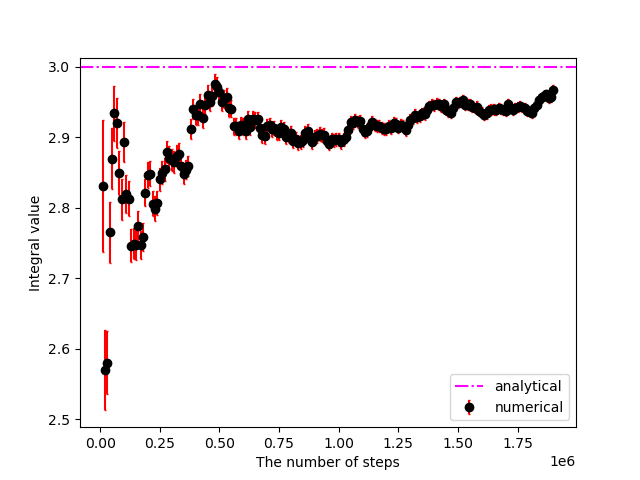
$${{\rm abs}((I_{\rm analytical} - I_{\rm numerical} )/I_{\rm analytical} ) \leq 0.01}$$かつ$${\delta \psi \leq 0.01}$$に収束するまでに1,904,335ステップを要した。
d. 今回実装した例では,収束に要するステップ回数はモンテカルロを用いた場合は分子動力学の半分程度となった。また,力学ベースで時間発展する分子動力学の方が$${\delta \psi}$$を過小評価する傾向があった。
Problem 7.5
$${\dot{\mathbf{x}}=\boldsymbol\eta(\mathbf{x})}$$に従うハミルトン方程式を考える。$${\mathbf{x}=\begin{bmatrix}q&p\end{bmatrix}^{\rm T}}$$とし,以下の式で時間発展を数値計算することを考える。
$$
\begin{align*}
\mathbf{x}(\Delta t)&=\mathbf{x}(0)+\Delta t\boldsymbol\eta\left(\mathbf{x}(0)+\frac{\Delta t}{2}\boldsymbol\eta(\mathbf{x}(0))\right)
\end{align*}
$$
このアルゴリズムに混合モンテカルロを組み合わせることができるか否かを理由を含めて述べよ。
時間発展の方程式が時間反転対称性を有すると仮定すると,
$$
\begin{align*}
\mathbf{x}(0)&=\mathbf{x}(\Delta t)-\Delta t\boldsymbol\eta\left(\mathbf{x}(\Delta t)-\frac{\Delta t}{2}\boldsymbol\eta(\mathbf{x}(\Delta t))\right)
\end{align*}
$$
が成立することになる。
この場合,
$$
\begin{align*}
\mathbf{x}(\Delta t)&=\mathbf{x}(0)+\Delta t\boldsymbol\eta\left(\mathbf{x}(0)+\frac{\Delta t}{2}\boldsymbol\eta(\mathbf{x}(0))\right)\\
&=\left\{\mathbf{x}(\Delta t)-\Delta t\boldsymbol\eta\left(\mathbf{x}(\Delta t)-\frac{\Delta t}{2}\boldsymbol\eta(\mathbf{x}(\Delta t))\right)\right\}+\Delta t\boldsymbol\eta\left(\mathbf{x}(0)+\frac{\Delta t}{2}\boldsymbol\eta(\mathbf{x}(0))\right)\\
\boldsymbol\eta\left(\mathbf{x}(\Delta t)-\frac{\Delta t}{2}\boldsymbol\eta(\mathbf{x}(\Delta t))\right)&=\boldsymbol\eta\left(\mathbf{x}(0)+\frac{\Delta t}{2}\boldsymbol\eta(\mathbf{x}(0))\right)\\
\mathbf{x}(\Delta t)-\frac{\Delta t}{2}\boldsymbol\eta(\mathbf{x}(\Delta t))&=\mathbf{x}(0)+\frac{\Delta t}{2}\boldsymbol\eta(\mathbf{x}(0))\\
\therefore \mathbf{x}(\Delta t)&=\mathbf{x}(0)+\frac{\Delta t}{2}\left\{\boldsymbol\eta(\mathbf{x}(0))-\boldsymbol\eta(\mathbf{x}(\Delta t))\right\}
\end{align*}
$$
$${\boldsymbol\eta(\mathbf{x}(0))-\boldsymbol\eta(\mathbf{x}(\Delta t))=\boldsymbol\eta\left(\mathbf{x}(0)+\frac{\Delta t}{2}\boldsymbol\eta(\mathbf{x}(0))\right)}$$が一般的には成立しないため,時間反転対称性の仮定が誤りであることが分かる。
以上より,与えられたハミルトン方程式は時間反転対称性を有さないため,混合モンテカルロを組み合わせることができない。
Problem 7.6
以下の二重井戸ポテンシャル$${U(x)}$$に対応するボルツマン分布をサンプルするためのレプリカ交換モンテカルロアルゴリズムを書け。
$$
\begin{align*}
U(x)&=D_0\left(x^2-a^2\right)^2
\end{align*}
$$
$${a=1}$$とし,$${D_0=5,10}$$の場合を検討せよ。各場合において,温度ラダー$${T_1,\cdots,T_M}$$,レプリカ数$${M}$$,交換試行の頻度を最適化せよ。$${M}$$個の各レプリカについてNose-Hoover-chainを用いて温度制御せよ。収束の測度である以下の量をプロットせよ。
$$
\begin{align*}
\zeta_k&=\frac{1}{N_{\rm bins}}\sum_{i=1}^{N_{\rm bins}}\left|P_k(x_i)-P_{\rm exact}(x_i)\right|
\end{align*}
$$
ここで,$${P_{\rm exact}(x)}$$は正解の確率分布,$${P_k(x)}$$は$${k}$$ステップ後の数値計算で得られた確率分布,$${N_{\rm bins}}$$は温度$${T_1}$$の系の計算結果をヒストグラムにした際のビン数を表す。
$${k_{\rm B}T_1=1}$$とした場合のpythonによる実装例を以下に示す。
from matplotlib import pyplot as plt
from scipy import integrate
import itertools
import numpy as np
np.random.seed(seed = 2023)
# Input parameters
n_step = 500000 # The number of step of numerical integration
interval = 100 # The interval of trying to exchange replicas
N_c = 4 # The number of decompotiosion for the operator exp(i * L_NHC * dt / 2)
dt = 0.001 # time step size
M = 2 # The number of chains
D0 = 5
beta = np.array([1., 0.75, 0.5, 0.2, 0.1, 0.05, 0.01, 0.004]) # Inverse temperatures
Q = 1 / beta # The time scale parameter for all chains
x_i = np.ones(len(beta)) # Initial position
p_i = np.random.normal(0, beta ** -0.5) # Initial momentum
eta = np.array([[0.0,] * M, ] * len(beta))
p_eta = np.array([[1.0,] * M, ] * len(beta))
# Seven weights of the Yodhida scheme for a sixth-order scheme
N_sy = 7
w = [0] * N_sy
w[0] = w[6] = 0.784513610477560
w[1] = w[5] = 0.235573213359357
w[2] = w[4] = -1.17767998417887
w[3] = 1 - 2 * np.sum(w[:3])
# Define functions
def U(x):
return D0 * (x ** 2 - 1.0) ** 2
def F(x):
return -4 * D0 * x * (x ** 2 - 1.0)
def exchangeReplicas(x, p, beta, start_index = 0):
for i in range(start_index, len(x) - 1, 2):
Delta = (beta[i] - beta[i + 1]) * (U(x[i]) - U(x[i + 1]))
A = np.min([1, np.exp(Delta)])
if A >= np.random.rand():
x0_new = x[i + 1]
p0_new = np.sqrt(beta[i + 1] / beta[i]) * p[i + 1]
x1_new = x[i]
p1_new = np.sqrt(beta[i] / beta[i + 1]) * p[i]
x[i] = x0_new
x[i + 1] = x1_new
p[i] = p0_new
p[i + 1] = p1_new
#print(f"Accepted: ({i},{i+1}) {A}")
#else:
#print(f"Rejected: ({i},{i+1}) {A}")
return x, p
def integrateNHC(p_now, eta, p_eta, beta):
for n_c, n_sy in itertools.product(range(N_c), range(N_sy)):
scale = np.ones(beta.shape)
KE = p_now ** 2
delta_j = w[n_sy] * dt / N_c
p_eta[:, M - 1] += 0.25 * delta_j * (p_eta[:, M - 2] ** 2 / Q - 1 / beta)
for m in range(M - 2, -1, -1):
p_eta[:, m] *= np.exp(-0.125 * delta_j * p_eta[:, m + 1] / Q)
if m == 0:
p_eta[:, m] += 0.25 * delta_j * (KE - 1 / beta)
else:
p_eta[:, m] += 0.25 * delta_j * (p_eta[:, m - 1] ** 2 / Q - 1 / beta)
p_eta[:, m] *= np.exp(-0.125 * delta_j * p_eta[:, m + 1] / Q)
scale *= np.exp(-0.5 * delta_j * p_eta[:, 0] / Q)
KE *= np.exp(-1.0 * delta_j * p_eta[:, 0] / Q)
for m in range(M):
eta[:, m] += 0.5 * delta_j * p_eta[:, m] / Q
for m in range(0, M - 1, 1):
p_eta[:, m] *= np.exp(-0.125 * delta_j * p_eta[:, m + 1] / Q)
if m == 0:
p_eta[:, m] += 0.25 * delta_j * (KE - 1 / beta)
else:
p_eta[:, m] += 0.25 * delta_j * (p_eta[:, m - 1] ** 2 / Q - 1 / beta)
p_eta[:, m] *= np.exp(-0.125 * delta_j * p_eta[:, m + 1] / Q)
p_eta[:, M - 1] += 0.25 * delta_j * (p_eta[:, M - 2] ** 2 / Q - 1 / beta)
p_now *= scale
return p_now, eta, p_eta
def conservedEnergy(x, p, e, p_e, b, q):
return 0.5 * p ** 2 + U(x) + 0.5 * np.sum(np.array(p_e) ** 2) / q + np.sum(e) / b
# Analytical result
q = np.linspace(-2.5, 2.5, 5001)
f_q = np.exp(-1 * U(q))
F_q = integrate.simps(f_q, q)
f_q /= F_q
# The below is the code
x_now = x_i
p_now = p_i
x0_list = []
zeta_list = []
for i in range(1, n_step + 1):
p_now, eta, p_eta = integrateNHC(p_now, eta, p_eta, beta)
p_now += 0.5 * dt * F(x_now)
x_now += dt * p_now
p_now += 0.5 * dt * F(x_now)
p_now, eta, p_eta = integrateNHC(p_now, eta, p_eta, beta)
if i % interval == 0:
if i % (2 * interval) == 0:
x_now, p_now = exchangeReplicas(x_now, p_now, beta, 1)
else:
x_now, p_now = exchangeReplicas(x_now, p_now, beta, 0)
x0_list.append(x_now[0])
if i % 5000 == 0:
# Hs = [conservedEnergy(x, p, e, p_e, b, q) for x, p, e, p_e, b, q in zip(x_now, p_now, eta, p_eta, beta, Q)]
hist, bins = np.histogram(x0_list, bins = 51, density = True)
ana = np.array([np.exp(-1 * U(0.5 * (bins[j] + bins[j + 1]))) / F_q for j in range(len(bins) - 1)])
zeta = np.mean(abs(hist - ana))
zeta_list.append([i, zeta])
print(i, zeta)
plt.plot(q, f_q, label = 'analytical')
plt.hist(x0_list, bins = 51, density = True, label = 'numerical')
plt.legend()
plt.xlabel('x')
plt.ylabel('density')
plt.savefig('x.png')
plt.figure()
zeta_list = np.array(zeta_list)
plt.plot(zeta_list[:,0], zeta_list[:,1], label = 'zeta')
plt.legend()
plt.xlabel('The number of step')
plt.ylabel('zeta')
plt.savefig('zeta.png')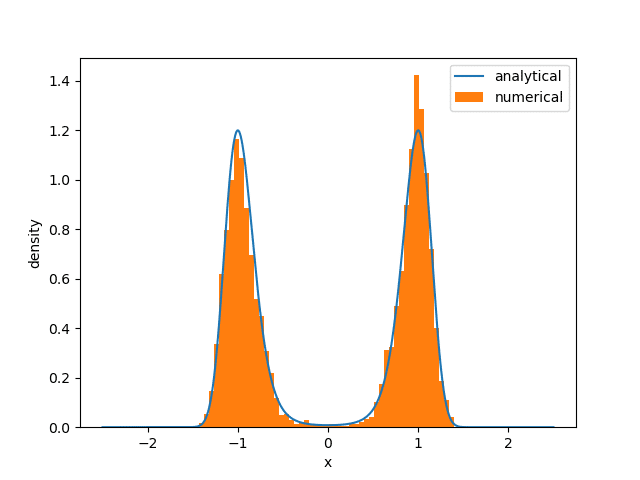
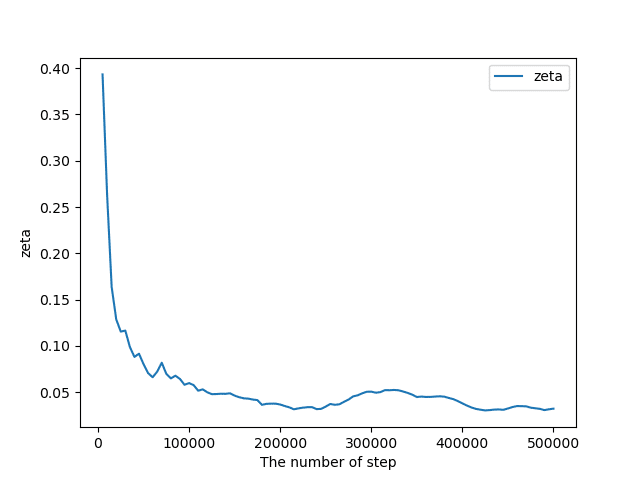
取り合えず適切にコーディングできていそうなので,$${D_0=10}$$の場合は省略。
Problem 7.7
4.10節で扱ったNose-Hoover-chainのような非ハミルトニアンの分子動力学アルゴリズムを,遷移パスサンプリングアルゴリズムの中でパス生成に使用することを考える。シューティングポイントを生成するための対称性を仮定($${\tau(\mathbf{y}_{j\Delta t}|\mathbf{x}_{j\Delta t})/\tau(\mathbf{x}_{j\Delta t}|\mathbf{y}_{j\Delta t})=1}$$)した場合,式(7.7.15)の受容ルールを以下のように修正しなければならないことを示せ。
$$
\begin{align*}
\Lambda[{\rm X}(\mathcal{T})|{\rm Y}(\mathcal{T})]&=h_{\mathcal{A}}(\mathbf{x}_0)h_{\mathcal{B}}(\mathbf{x}_{n\Delta t})\min\left[1,\frac{f(\mathbf{x}_0)}{f(\mathbf{y}_0)}\frac{J(\mathbf{y}_{j\Delta t};\mathbf{y}_0)}{J(\mathbf{x}_{j\Delta t};\mathbf{x}_0)}\right]
\end{align*}
$$
ここで,$${J(\mathbf{x}_{t};\mathbf{x}_0)}$$は式(4.9.2)で計算される変換$${\mathbf{x}_0\rightarrow \mathbf{x}_t}$$のヤコビアンである。
微小体積内の確率の保存を考えると,非ハミルトニアンの場合の$${f(\mathbf{x}_{j\Delta t})}$$は
$$
\begin{align*}
f(\mathbf{x}_{j\Delta t})&=\left\{\frac{T(\mathbf{x}_{j\Delta t}|\mathbf{x}_{(j-1)\Delta t})}{J(\mathbf{x}_{j\Delta t};\mathbf{x}_{(j-1)\Delta t})}\right\}f(\mathbf{x}_{(k-1)\Delta t})\\
&\vdots\\
&=\left\{\frac{\prod_{i=0}^{j-1}T(\mathbf{x}_{(i+1)\Delta t}|\mathbf{x}_{i\Delta t})}{\prod_{i=0}^{j-1}J(\mathbf{x}_{(i+1)\Delta t};\mathbf{x}_{i\Delta t})}\right\}f(\mathbf{x}_{0})\\
&=\left\{\frac{\prod_{i=0}^{j-1}T(\mathbf{x}_{(i+1)\Delta t}|\mathbf{x}_{i\Delta t})}{J(\mathbf{x}_{j\Delta t};\mathbf{x}_0)}\right\}f(\mathbf{x}_{0})\\
&=\left\{\frac{f(\mathbf{x}_{0})}{J(\mathbf{x}_{j\Delta t};\mathbf{x}_0)}\right\}\prod_{i=0}^{j-1}T(\mathbf{x}_{(i+1)\Delta t}|\mathbf{x}_{i\Delta t})\\
\end{align*}
$$
となるため,式(7.7.15)の$${f(\mathbf{x}_0), f(\mathbf{y}_0)}$$をそれぞれ$${f(\mathbf{x}_0)/J(\mathbf{x}_{j\Delta t};\mathbf{x}_0), f(\mathbf{y}_0)/J(\mathbf{y}_{j\Delta t};\mathbf{y}_0)}$$に置き換えればよい。
参考文献
Mark Tuckerman, Statistical Mechanics: Theory and Molecular Simulation (Oxford Graduate Texts)
