Funnel Metadynamics
Funnel metadynamicsは2分子間の結合自由エネルギーを定量的に求めることを目的に提案された分子シミュレーション手法の一種です。言葉通りFunnel型のrestraint potentialでサンプリング領域を制限したmetadynamicsを実行します。restraint potentialはサンプリング領域を制限する以外にも結合定数に関して具体的に計算可能な表式を得る意味合いもあります。本記事ではFunnel metadynamicsの背景理論を説明します。
平均力ポテンシャルを用いた結合定数の表記
議論の出発点は平均力ポテンシャルを用いて定義された結合定数$${K_b}$$になります。
$$
\begin{align*}
K_b&=\frac{\int{\rm d}\mathbf{r}H_{\rm site}(\mathbf{r}){\rm e}^{-\beta W_{xyz}(\mathbf{r})}}{{\rm e}^{-\beta W_{xyz}(\mathbf{r}_{\rm bulk})}}\\
&=\int{\rm d}\mathbf{r}H_{\rm site}(\mathbf{r}){\rm e}^{-\beta\left\{W_{xyz}(\mathbf{r})-W_{xyz}(\mathbf{r}_{\rm bulk})\right\}}\\
\end{align*}
$$
$$
\begin{align*}
\mathbf{r}&:分子間の相対位置を特徴づける3次元座標(例:重心間ベクトル)\\
\mathbf{r}_{\rm bulk}&:分子間距離が平均力ポテンシャルが一定値を取る程度に十分に離れた領域\\
W_{xyz}(\mathbf{r})&:\mathbf{r}の平均力ポテンシャル\\
H_{\rm site}(\mathbf{r})&:結合領域で1,それ以外で0の値を取る関数\\
\beta&:逆温度
\end{align*}
$$
$${K_b}$$を計算するためには$${H_{\rm site}(\mathbf{r})}$$の情報を得る必要がありますが,$${H_{\rm site}(\mathbf{r})}$$を具体的に評価するのは困難です。そこでFunnel metadynamicsでは,$${H_{\rm site}(\mathbf{r})}$$の領域を包含するFunnel型のrestraint potentialを設けることにより,$${H_{\rm site}(\mathbf{r})}$$の具体的な表式なしでも結合領域の情報を(積分された形で)得られるような手法に落とし込みます。
Funnel型のrestraint potential
Metadynamics計算中に以下の形状のrestraint potentialが課せられることにより,緑色の領域のみがサンプリングされる状況になります。

計算結果を解析する際には,Funnel型のrestraint potentialの補正項を設けることはせず,緑色の領域のサンプリング情報から結合定数$${K_b}$$の情報を得ることを考えます。
以下では,緑色の領域を$${H_{\rm funnel}(\mathbf{r})}$$と表現することにします。
1次元平均力ポテンシャルの導出
次に$${W_{xyz}(\mathbf{r})}$$を$${x,y}$$に関して積分することにより,funnelの軸方向(z軸方向)に対する1次元平均力ポテンシャル$${W_{z}(z)}$$を計算することを考えます。
$$
\begin{align*}
\rho_{xyz}(\mathbf{r})&=\frac{{\rm e}^{-\beta W_{xyz}(\mathbf{r})}}{\int{\rm d}\mathbf{r}{\rm e}^{-\beta W_{xyz}(\mathbf{r})}}\\
\rho_{z}(z)&=\int{\rm d}x\int{\rm d}y\rho_{xyz}(\mathbf{r})\\
&=\frac{\int{\rm d}x\int{\rm d}y{\rm e}^{-\beta W_{xyz}(\mathbf{r})}}{\int{\rm d}\mathbf{r}{\rm e}^{-\beta W_{xyz}(\mathbf{r})}}\\
&=\frac{{\rm e}^{-\beta W_{z}(z)}}{\int{\rm d}z{\rm e}^{-\beta W_{z}(z)}}\\
\therefore {\rm e}^{-\beta W_{z}(z)}&=\left\{\frac{\int{\rm d}z{\rm e}^{-\beta W_{z}(z)}}{\int{\rm d}\mathbf{r}{\rm e}^{-\beta W_{xyz}(\mathbf{r})}}\right\}\int{\rm d}x\int{\rm d}y{\rm e}^{-\beta W_{xyz}(\mathbf{r})}\\
&=\left\{\frac{\int{\rm d}z{\rm e}^{-\beta W_{z}(z)}}{\int{\rm d}\mathbf{r}{\rm e}^{-\beta W_{xyz}(\mathbf{r})}}\right\}\left[\int{\rm d}x\int{\rm d}yH_{\rm funnel}(\mathbf{r}){\rm e}^{-\beta W_{xyz}(\mathbf{r})}+\int{\rm d}x\int{\rm d}y\left\{1-H_{\rm funnel}(\mathbf{r})\right\}{\rm e}^{-\beta W_{xyz}(\mathbf{r})}\right]\\
&=:C\int{\rm d}x\int{\rm d}yH_{\rm funnel}(\mathbf{r}){\rm e}^{-\beta W_{xyz}(\mathbf{r})}
\end{align*}
$$
ここで,$${C}$$は$${z}$$に依存しない定数です。
Funnel restraint potentialの存在下では右辺の第2項はサンプリングされないため,式から除外することができます。
$${W_z(z)}$$が$${z_{\rm bulk}\geq z_{\rm cc}}$$で$${0}$$になるように選ぶことにします。
また,$${z\geq z_{\rm cc}}$$では$${W_{xyz}(\mathbf{r})}$$が$${x,y}$$に依存しないことを考慮すると,
$$
\begin{align*}
{\rm e}^{-\beta W_{z}(z_{\rm bulk})}&=C\int{\rm d}x\int{\rm d}yH_{\rm funnel}(\mathbf{r}){\rm e}^{-\beta W_{xyz}(0,0,z_{\rm bulk})}\\
&=C{\rm e}^{-\beta W_{xyz}(0,0,z_{\rm bulk})}\int{\rm d}x\int{\rm d}yH_{\rm funnel}(\mathbf{r})\\
&=C{\rm e}^{-\beta W_{xyz}(0,0,z_{\rm bulk})}\pi R_{\rm cyl}^2\\
&=1\\
\therefore C&=\frac{{\rm e}^{\beta W_{xyz}(0,0,z_{\rm bulk})}}{\pi R_{\rm cyl}^2}
\end{align*}
$$
以上より,$${W_{z}(z)}$$に関して以下の表式を得ることができました。
$$
\begin{align*}
{\rm e}^{-\beta W_{z}(z)}&=\frac{1}{\pi R_{\rm cyl}^2}\int{\rm d}x\int{\rm d}yH_{\rm funnel}(\mathbf{r}){\rm e}^{-\beta\left\{W_{xyz}(\mathbf{r})-W_{xyz}(0,0,z_{\rm bulk})\right\}}
\end{align*}
$$
1次元平均力ポテンシャルを用いた結合定数の表式
冒頭で出てきた結合定数$${K_b}$$の式を1次元平均力ポテンシャル$${W_{z}(z)}$$で表すことを考えます。
$$
\begin{align*}
K_b&=\int{\rm d}\mathbf{r}H_{\rm site}(\mathbf{r}){\rm e}^{-\beta\left\{W_{xyz}(\mathbf{r})-W_{xyz}(\mathbf{r}_{\rm bulk})\right\}}\\
&=\int{\rm d}\mathbf{r}H_{\rm funnel}(\mathbf{r}){\rm e}^{-\beta\left\{W_{xyz}(\mathbf{r})-W_{xyz}(\mathbf{r}_{\rm bulk})\right\}}-\int{\rm d}\mathbf{r}\left\{H_{\rm funnel}(\mathbf{r})-H_{\rm site}(\mathbf{r})\right\}{\rm e}^{-\beta\left\{W_{xyz}(\mathbf{r})-W_{xyz}(\mathbf{r}_{\rm bulk})\right\}}\\
&=\int_{z_{\rm min}}^{z_{\rm max}}{\rm d}z{\rm e}^{-\beta W_{z}(z)}-\int{\rm d}\mathbf{r}\left\{H_{\rm funnel}(\mathbf{r})-H_{\rm site}(\mathbf{r})\right\}\\
&\simeq\int_{z_{\rm min}}^{z_{\rm max}}{\rm d}z{\rm e}^{-\beta W_{z}(z)}
\end{align*}
$$
$${z_{\rm min}, z_{\rm max}}$$は結合領域のz軸方向に対する定義域です。右辺第2項は右辺第1項と比較して積分値にほぼ寄与しない大きさなので,近似しても精度に影響しないことが期待されます。
結合定数が求まれば,結合自由エネルギーを求めるのは簡単です。
$$
\begin{align*}
\Delta G^0&=-\frac{1}{\beta}\ln\left(\frac{K_b}{V^0}\right)\\
&=-\frac{1}{\beta}\ln\left(\frac{K_b}{1660\AA^3}\right)
\end{align*}
$$
実用上のいくつかの注意点
実用上は$${z_{\rm max}}$$をどう決めるかは意外と難しいです。1次元平均力ポテンシャルの形状がプラトーになるところが$${z_{\rm max}}$$ではないことにご注意ください。
決め方の一つとして,$${z}$$軸からの距離$${\rho=\sqrt{x^2+y^2}}$$の値を調べるということが挙げられます。Funnelが広がるにつれて$${\rho}$$の値も大きくなりえますが,結合領域ではFunnel restraint potentialがあるにも関わらず$${\rho}$$は大きな値を取れなくなります。
それを表した論文の図を以下に示します。
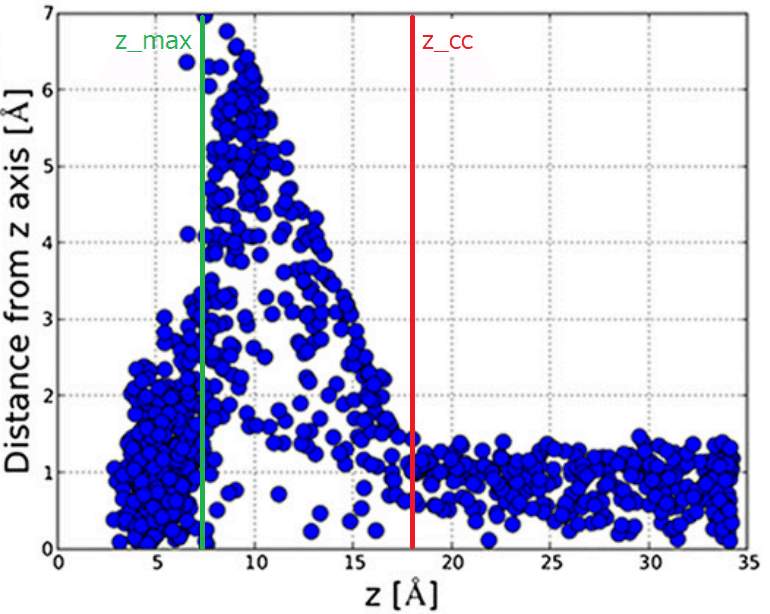
$${z_{\rm cc}}$$の値をユーザー側で決めなければいけないパラメータです。理論的には$${z_{\rm cc}}$$以降は1次元平均力ポテンシャル$${W_{z}(z)}$$の形状はプラトーになるはずですので,計算した結果そうなっていない場合は,$${z_{\rm cc}}$$をより大きな値に設定して計算すべきです。
幸いにも積分値である$${K_b}$$の値は$${z_{\rm max}}$$と$${z_{\rm cc}}$$の両方に対してそれほど敏感ではないため(とは言ってもいい加減にきめていいというわけではありません),パラメータチューニングが実用上それほど問題にはならないかもしれません。
metadynamicsは1次元平均力ポテンシャル$${W_{z}(z)}$$を決める役割がありますが,1CVのmetadynamicsに限定する必要はありません。最終的に$${W_{z}(z)}$$を求めればよいので,複数CVを設定しても問題ありませんし,極論を言えば複数CVに$${z}$$が含まれていなくても(それが効率的であるかどうかは置いておいて)成立します。
さらに極論を言えば,metadynamicsでサンプリングする必要性すらありませんので,アンブレラサンプリング等のその他のサンプリング手法とFunnel restraint potentialを組み合わせることも可能です。
