
【関数解析】連続関数空間における完備性の話
今回も機械学習で利用される数学の記事です。その中で、関数解析の序盤に登場するバナッハ空間のための、連続関数空間とその完備性についての話をします。というのも、随分前に関数解析の勉強を始めたものの、連続関数空間における完備性の正体について靄がかった状態が続いたのですが、それが最近になってようやく晴れてきたということがあり、備忘録も兼ねてこの辺の概念をまとめてみようと思います。また、関数解析は学部で学ぶ基礎的な数学の分野から見ると、一気に専門性が増すため、特に大人になって学び直すという方が導入部分で挫折してしまうということも少なくないでしょう。そのような方の学習を少しでも助けられたらなという思いも込めて記事を書きます。
記事の構成
この記事の目的は連続関数空間における完備性の正体を掴み、連続関数空間をバナッハ空間とすることです。しかしながら、連続関数空間の完備性を言うためには抽象的な数学の構造を積み上げていく必要があります。そのために、次の4つのステップに話題を分けて、必要な概念や構造を順次ピックアップしていくような構成で話を進めたいと思います。(なお、解析学の初等概念を何の説明もなく利用します。)
1. 実数の完備性
2. 線形ノルム空間の定義
3. 連続関数空間の定義
4. 連続関数空間の完備性
ステップ1, 2はステップ3,4のための言葉や概念の準備です。よって、これらについて分かっている方は読み飛ばしてしまって構いません。
1. 実数の完備性
実数の完備性は実数の連続性の公理で認められているもの1つで、これも実数の連続性を言うためのものです。実数の完備性はコーシー列の収束により示されます。まず、コーシー列の定義が次となります。
定義 1.1
数列{x_n}がコーシー列であるとは、任意のε > 0に対して、ある自然数Nが存在して、任意のm, n > Nに対して、|x_m - x_n| < ε が成り立つことである.
コーシー列の収束の判定方法は数列の収束の定義(ε-N論法)に似ています。しかし、ε-N論法はある極限値αが既に分かっていたときに、その数列がαに収束することを確かめるために利用しますが、一方でコーシー列の判定は極限値が分からなくても、その数列(点列)が収束することを判定する方法として利用されます。
このコーシー列を使った実数の完備性を示す公理が次です。
公理 1.2
実数からなるコーシー列{x_n} は、必ずある実数αに収束する。
この、{x_n}がコーシー列であると必ずある実数値に収束するという性質を実数の集合Rの完備性といいます。実数の完備性の重要な点は、{x_n}がコーシー列であることが{x_n}の収束のための必要十分条件であることで、極限値が予め分からなくとも{x_n}がコーシー列であれば{x_n}はある実数に必ず収束するということです。
ただ、この公理だけでは完備の概念自体が伝わりづらいと思いますので、次に、コーシー列ではあっても、完備ではない例を見てもらいたいと思います。(Wikipediaからの引用です。)
有理数全体の成す集合に差の絶対値によって定義される標準距離函数を備えた空間 ℚ はℚ 上完備でない。例えば
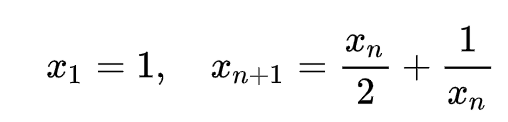
で定義される列を考えると、これは有理コーシー数列だが如何なる有理数にも収束しない。実際、これが何らかの有理数 x に収束するならば、x は x^2 = 2 を満たさねばならないが、これを満たす有理数は存在しない。しかしながら、同じ列を実数列と考えるならば無理数である √2 を極限に持つ。
このことを読み解くと、実数および有理コーシー列では次の相違が見られます。
・実数からなるコーシー列{x_n} は、必ずある実数αに収束する
・有理数からなるコーシー列{x_n} は、有理数βに収束しない場合もある
つまり完備を考える上で、ある空間の任意のコーシー列がもとの空間の点に収束するということが非常に重要であることが分かります。
以後、このコーシー列の収束という概念を使い、連続関数空間の完備性を考えていきます。
2. 線形ノルム空間の定義
連続関数空間に入る前に、少しだけ抽象的な話をします。というのも、これから実数や有理数の集合よりももっと複雑な連続関数空間に完備という概念を導入するわけですが、そのためにコーシーの条件を使いたいので、連続関数空間においてもコーシー列を作る必要があります。実数の場合では、コーシー列の作成において、2つの項の差の絶対値がεで抑えられるという判定方法を取っていました。しかし、一般に数学で考えるような種々の空間はより複雑であり単純な項の差では距離を測れないことがほとんどで、それは連続関数空間においても同様です。このことから、以後は一般的な線形空間Xを考察の対象とし、ノルムや距離を導入することとします。(なぜ線形空間とするかはステップ3で明らかになります。)その後、Xにおけるコーシー列の定義を行うことをしていきたいと思います。
では、まず一般の線形空間にノルムを導入し、これを線形ノルム空間とするところからスタートしましょう。
定義 2.1: 線形空間の条件
x, y, z ∈ X, a, b ∈ R とする。
(V 1) (x + y) + z = x + (y + z)
(V 2) x + y = y + x
(V 3) 0 + x = x + 0 = x
(V 4) 任意のxに対して、逆元-xが存在して、
x + (-1)x = x + (-x) = (-x) + x = x
(V 5)
(a) a(x + y) = ax + ay
(b) (a + b)x = ax + ay
(c) (ab)x = a(bx)
(V 6) 1 · x = x
これら(1)-(6)を線形空間の公理と認めると、
0x = 0
が成立する。
※注意: 線形代数では、具体的な線形空間R^nが線形空間の条件を満たすことを学びましたが、ここで扱う線形空間はより一般的な定義となります。つまり、ある集合Aの元がベクトルでなくても、すべての元についてこの条件が成立すればAは線形空間になります。次に、線形ノルム空間を定義します。
定義 2.2: 線形ノルム空間の定義
線形空間Xの任意の元xに対して、一つの実数を対応させる関数||x||が次の条件を満たすとき、関数 ||·||をノルムという。
(N 1) Xの任意の元xに対して、||x|| ≧ 0 かつ ||x|| = 0となるのは、x = 0 のときのみ
(N 2) Xの任意の元xおよび、任意の複素数aに対して ||ax|| = |a|||x|| が成立する
(N 3) Xの任意の元x, yに対し、三角不等式
||x + y|| ≦ ||x|| + ||y||
が成立する。
このようなノルムが導入された線形空間を線形ノルム空間という。
ノルムの最も重要な性質として(N 3)の「分解すると大きくなる」というものがあります。また、ここでも注意点として、いわゆるR^nやC^nといった線形代数で扱う線形空間に、内積によってノルムを導入した線形空間は、具体的な線形ノルム空間の一例であって、ここでいう線形ノルム空間はさらに抽象度が高いものとなっています。つまり、内積によるノルムではなくとも、N 1, N 2, N 3を満たすノルムであれば何でも良いということです。また、次の定理は記事の後半で使う重要な定理で、ノルムの性質を知る上で抑えておく必要があります。
定理: ノルムの連続性
ノルム||·||は連続関数である。すなわち、ノルム空間Xの点列{x_n}が極限x_0に収束するなら、数列{||x_n||}は極限値||x_0||に収束する。(証明略)
このようなノルムを定義することで、空間Xに距離を入れることができます。例えば、次の距離は我々に馴染み深い、線形空間R^nにおけるベクトルどうしの距離です。(高校で習う2点間の距離のn次元バージョンです)

この距離はノルムによって定義されるので、ノルムから導かれる距離といいます。(※ すべての距離関数dは距離の定義を満たす必要があります。)
我々の現在の目的は、ノルム空間Xでコーシー列を作ることでした。ここまでで、ノルムと距離の概念を導入できましたので、まずは実数列のコーシー列の収束の定義がノルム空間Xでも言えると仮定してみましょう。
命題 2.3
ノルム空間Xの点列{x_n} (n=1, 2, ····, ∞)が収束するための必要十分条件は、任意のε > 0に対してある自然数Nが存在して、任意のm, n > Nに対して
||x_m - x_n|| < ε が成り立つことである.
実数の完備性を示すために用いたコーシー列との差分は
・実数列がノルム空間上の点列になった
・2つの元の距離のとり方が、ノルムを用いた距離になった
の2つです。
そして、この命題は次のように言い換えることができます。
命題 2.3'
ノルム空間Xの点列{x_n}が収束するための必要十分条件は、{x_n}がコーシー列となることである。これをさらに簡潔に言うなら、
「ノルム空間Xの収束する点列はコーシー列である。」
<証明>
x_n -> xとなるとき、任意のε > 0に対して、m, nを十分大きく取れば
||x_m - x|| < ε/2, ||x_n - x|| < ε/2
となる. ノルムは三角不等式を満たすから
||x_m - x_n|| = ||x_m - x + x - x_n|| ≦ ||x_m - x|| + ||x - x_n|| < ε
とできる。
この証明は完備を示す十分条件にもなっているでしょうか?..........
答えはNoです。というのも、実数Rにおいてはコーシー列は実数値に収束しました。しかし、この証明では、コーシー列になることは示せても、収束先がXに属するかを言えていないのです。つまり、現時点では、まだ完備性を言うことができないのです。
今は抽象的な空間で議論を進めていますので、具体的な線形空間にノルムを導入し、このコーシー列の判定条件を考えるようなことをしていきましょう。その具体的な空間というのがいよいよ登場の連続関数空間です。
3. 連続関数空間の定義
連続関数空間のもととなるのは連続関数全体の集合です。数学で連続関数空間を表す際には、C(I)と書かれます。Iは解析学ではおなじみの区間のことで、I = [a, b], I = (a, b), I = [a, b)などと書かれるものですね。以降の解説ではこの連続関数の空間をC[a, b]と表記します。C[a, b]の構成を次のようにします。有界閉区間[a, b]の点tに実数値f(t)を対応させる関数を
![]()
で表し、[a, b]上の各点tで連続である関数fの全体をC[a, b]で表します。(まだこのとき、C[a, b]は集合です。)このような定義や言い回しはストレスを感じる人もいるかと思いますが、連続関数空間の構造を我々の既知の知識で捉えやすくすることに役立ちます。というのも、このように定義された連続関数全体の集合は、線形空間の公理(定義 2.1)をうまく満たしてくれるのです。
連続関数空間が線形空間の公理を満たすこと
(C 1) fとgの和 f + g を (f + g)(t) = f(t) + g(t) (tは変数)
(C 2) スカラー倍afを (af)(t) = a · f(t)
で定義するとf + g, afが[a, b]上の連続関数になることはよく知られてる。
したがって、f + g ∈ C[a, b], af ∈ C[a, b] となる。
このことから、結合法則や交換法則が成り立つことは明らかです。ここで、追加の定義を行います。
(C 3) f = gであるとは有界閉区間[a, b]で取りうる任意の変数tについて
f(t) = g(t)
(C 4) 0 ∈ C[a, b]を 0(t) = 0 と定義する
これらの(C 1) - (C 4)の定義の元、連続関数空間C[a, b]は線形空間の公理を満たし、線形空間となります。
連続関数空間の次元について
なお、線形空間における重要な概念の一つである次元について、連続関数空間においてはその次元は無限となります。このことについての細かい証明等は割愛させていただきますが、次のことを考えれば納得できるかと思います。まず、もともとのC[a, b]は連続関数全体の集合ですから、例えばsin(x)の∞次近似のマクローリン展開も連続関数で、C[a, b]に含まれていることになります。したがって、この多項式をベクトル表示すればn=∞の項のベクトルの次元は無限となるということです。
これらのことがステップ2において、線形ノルム空間を先に説明した理由でした。(関数は複雑ですが、ベクトルのように扱うことができれば、もろもろの性質の調査が容易になりますよね)では、ステップ2の最後で行ったコーシー列の判定条件を連続関数空間C[a, b]において考えていきましょう。
4. 連続関数空間の完備性
4.1 連続関数空間におけるコーシー列
連続関数空間におけるコーシー列の実体は関数列です。関数列に対してコーシー列の収束を考えるために、まずは具体的な関数列を例にしてみましょう。そこで、C[a, b]上のひとつのコーシー列の候補として次のような関数列を用意します。
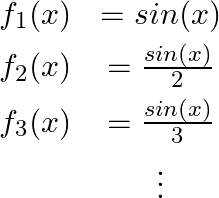
すなわち
![]()
となる関数列{f_n}を考えます。この関数列がコーシー列となるためには、距離を入れてあげる必要があります。そのために、定義 2.2を満たす、L^2ノルムというノルムを導入します。(いわゆるユークリッドノルムを一般化した、つまり関数に関して考えたものですね。)定義は次となります。
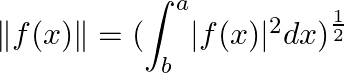
さて、関数列{f_n}は、このL^2ノルムを持ってコーシー列となるでしょうか? 実際に手を動かしてみましょう。ここで、区間をI=[0, 2]とします。

がコーシー列を示すための2つの関数の距離です。(平方根を消すために2乗しています)この距離を抑えられるようなεを探していきましょう。右辺における分母のsin^2xは半角の公式より、(1 - cos2x)/2ですから積分のための関数は次のように変形できます。
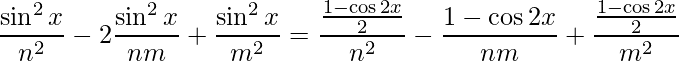
この関数を定積分すれば、f_mとf_nの距離は

で抑えることができます。(1/4 sin4 ≒ -0.189200623826982を利用しています。)
(n, m -> ∞)のとき任意のx ∈ [0, 2]に対して、||f_m - f_n|| -> 0となることからコーシー列です。従って、実数の完備性よりlim_{n -> ∞} f_n(x)となる極限の関数が存在します。これを f_0(x)とおくと 次に示したいのはf_0 ∈ C[0, 2]となるかです。C[0, 2]は連続関数全体の集合より、f_0 ∈ C[0, 2]となることとf_0が任意のx ∈ [0, 2]で連続であることは同値です。実際、すべてのx ∈ [0, 2]においてf_0(x) = 0となりますから、f_0は連続でf_0 ∈ C[0, 2]が分かります。(一般にはε-δ論法を使って厳密に連続性を示す必要があります)つまり、{f_n}はL^2ノルムにおいてC[0, 2]に収束するコーシー列です。
余談となりますが、次のグラフは (n = 1, 3, 5, ···· 301, m = 2, 4, 6, ····, 300)における(L^2ノルムを用いた)||f_m - f_n||の値とそのn, mにおけるεの関係をグラフにしたものです。このグラフの描画用コードはこちら

n, m <= 200くらいまでは||f_m - f_n||がεで抑えられていることが分かりますが、n, m > 200では双方のグラフが被ってしまっていて関係性が見にくくなってしまっています。よって、n, m > 200だけに絞って見やすくしたグラフが次です。

このグラフが表すように、||f_m - f_n||は1から300までのすべてのn,mにおいてεで抑えられていることが分かります。コーシー列は、このあと(n, m -> ∞)としてもこの関係性が変わらないまま収束する数列を指しているのです。
L^2ノルムはC[0, 2]上で完備なノルムとなるかを示すために、もうひとつくらいC[0, 2]から関数列を取りましょう。それを次とします。
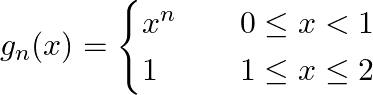
{g_n}がコーシー列であるとすれば、I = [1, 2]のとき||g_m - g_n|| = 0となります。一方、I = [0, 1)においては広義積分で次のように展開できます。

これらの結果から、{g_n}も(n, m -> ∞)のとき||g_m - g_n|| -> 0となるためコーシー列です。では、g_nの(n -> ∞)における極限の関数g_0はg_0 ∈ C[0, 2]となるかを調べましょう。f_0同様に、g_0の連続性を考えればいいです。g_0は、0 ≦ x < 1のとき0、1 ≦ x ≦ 2のとき1を取る関数だから不連続となり、なんとg_0 ∉ C[0, 2]です。つまり、L^2ノルムではC[0, 2]上に収束しないコーシー列が存在してしまうのです。
(※ 関数列{g_n)}はL^2空間においては収束するコーシー列となります。)
空間が完備となるには、任意のコーシー列がもとの空間の元に収束する必要がありますから、ノルム空間の条件とノルム空間におけるコーシー列の判定条件だけでは、やはり完備性の十分条件にならないということが具体的にも判明しました。ここでもう一度実数の完備性に着目してみると、実数の完備性においては(絶対値ノルムによる)コーシー列の収束そのものが完備性の必要十分条件となっていました。よって、連続関数空間C[a, b]においてもコーシー列の収束そのものが完備性の必要十分条件となるようなノルムを今一度考えてみましょう。L^2ノルムの問題は極限の関数がC[a, b]に収束しなかったことでした。つまり、任意のコーシー列について、極限の関数が連続であることを保証できるようなノルムであるなら、コーシー列の収束そのものが完備のための必要十分条件となりそうです。
4.2 連続関数空間の一様ノルム
C[a, b]に次のノルムを導入します。(I = [a, b]です。)
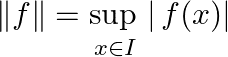
このノルムを一様ノルムといいます。直感的には、L^2ノルムのように定義域に依存して値が決まるのではなく、関数に対して一意的に値が求まることから、このノルムが完備を言うために機能することはなんとなくイメージできるでしょう。また、有界閉区間上の関数の最大値の存在性は、最大値最小値の定理により保証されているため、このノルムのsupはmaxと一致します。
次にこのノルムが完備となることを示さなければいけませんが、先にネタバレをしてしまうと、このノルムはノルムの条件を満たし、さらに完備であることが言えます。なお、証明をすべて書くと長くなってしまうので、証明の方針だけ抑えます。(参考文献[1]のP15で具体的な証明が行われています。その他にもweb上の文献でこの証明は多く取り扱われています。)
証明の方針
■ノルムの条件を満たすこと
(N 1), (N 2)の証明は容易です。(N 3)が成立することは、f, g ∈ C[a, b]に対して |f(x) + g(x)| ≦ |f(x)| + |g(x)| ≦ ||f|| + ||g||が任意のxで言える。=> 左辺のsupをとれば、||f + g|| ≦ ||f|| + ||g||. で示される。
■完備であること
(1) C[a, b]の関数列{f_n}が一様ノルムについて、コーシー列であること
(2) {f_n}がC[a, b]に収束すること
実数の完備性よりlim_{n -> ∞} f_n = f_0が存在するから、f_0 ∈ C[a, b]
と||f_n - f_0|| -> 0 (n -> ∞) を示せば良い。つまり、次の2つを示す。
(2.1) f_0 ∈ C[a, b]はf_0が任意のx ∈ [a, b]で連続であること
(2.2) ||f_n - f_0|| -> 0は、sup |f_n(x) - f_0(x)| = 0 (n -> ∞) となること
特に(2.2)は、{f_n(x)}は一様収束することを言っています。つまり、連続関数空間において、任意の{f_n}が収束するコーシー列であるのと、関数列{f_n}が一様収束することは同値なのです。一様収束であれば、収束先の関数も連続であることが保証されるので、f_0 ∈ C[a, b] がいえます。
その他にも、C[a, b]では、ワイエルシュトラスの定理なども成立します。ワイエルシュトラスの定理の成立により、閉区間上の連続関数のなす集合において、多項式からなる部分集合は一様ノルムの誘導する距離に関して稠密であることが示されます。 => そのような連続関数に対しては一様収束する多項式列が存在する。
このことは、例えば指数関数e^xやsin(x), cos(x)などのマクローリン展開による無限次近似の関数列を考えれば、これらが一様収束であることが分かるでしょう。つまり、これらの関数列はコーシー列でもあります。
これらのことから、一様ノルムが入ったC[a, b]のコーシー列は必ずもとの空間に収束するため、コーシー列の判定条件が完備のための必要十分条件となるのです。(4.1のg_0のような関数はこの空間に含まれないことが予め保証されている)
そして、C[a, b]は一様ノルムに関し、バナッハ空間(完備なノルム空間)になります。これが、連続関数空間の完備性の正体です。完備を使えば有限次元における線形代数と同様の概念を関数空間に持ち込むことや、近似の程度が分かることから数値計算などにも応用可能になります。これが後々のフーリエ解析の土台となります。
参考文献
[1] 洲之内 治男 [関数解析入門] サイエンス社
[2] 小川英光 [工学系の関数解析] 森北出版株式会社
