「図学」を使ってイラスト制作
今でこそ「アカデミック・ハラスメント」なんて言葉もあるが、我々の学生時代、教授とは「学生を虐める生き物」というのが仲間内の共通認識だった。殊に必修科目を受け持つ教授の残虐な振る舞いは、口にするのも憚るくらい非道なものだったと思う。
図学を受け持つO先生の講義も苦行の時間で、講話の後に出題される演習問題が我々のメンタルをズタズタに引き裂いた。なにしろ出題はすべて先生のお手製で、どんな参考書を探しても答えは載ってない。時間終了とともに提出し、次の講義の最初に返却される。そして正解者の数を発表すると(毎回2~3名ほどしか…)「こんなんじゃ単位はあげられないよ?」と小言を漏らし板書を始める。「去年の方がまだマシだった」なんて事も言ってたっけ。
図学というのは、作図法によって図形問題を解くという学問。先日の共通テストで数学の問題に定規を使い、失格になった受験生がいたけれど、実務で設計やってる者としては定規を使い、正確に作図して対象を明確化するのは当たり前の行為と言いたくなる。でもO先生は紐を使って黒板に作図してましたが。
図学の基礎となる「投象法」(今は投影法っていうのかも?)を説明します。まず3次元空間に直線があります。直線はX・Y・Z軸に沿わずフリーな角度で置かれている。コイツをXY平面、XZ平面に投影した画を並べると、こんな感じになります。

投影された直線の端と端は、投象線を境に垂線上に並んでいる。しかしこの画ではYZ平面上に投影されるであろう角度が盛り込まれていないため、線の長さをこのまま測っても実際の長さ(実長)はわからない。そこで実長がわかるよう副投影図を作図して、そこから実長を求めます。
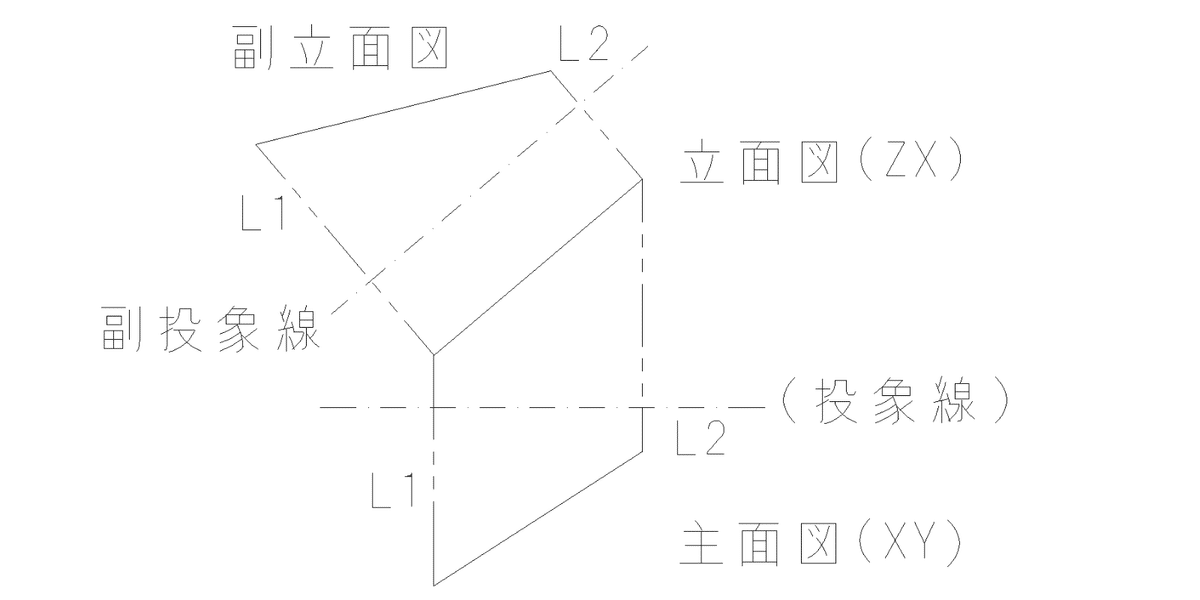
立面図(XZ平面)に描かれた直線と、平行な副投象線を作図する。主面図(XY平面)から、投象線との距離(L1、L2)を測定し、それぞれ副投象線の向こうにあてがい、そこから直線を作図する。この直線が、求める実長を示します。これが副投象法という解法です。
以前、イラストの背景にテトラポットを使おうと思い、3Dでモデリングを試みたのですが、4つの突起をそれぞれ120度に配置してみたら何かおかしい。調べてみるとテトラポットの突起は「正四面体」の頂点にあわせて配置している、と。自力で計算を試みたのですが途中で挫折、ネットにあった値を使ってはみたのですがどうも落ち着かない。そうだ「図学」で答えが出せないかな?と…
O先生のご指導で、有意義な技術を身に着けることができました。「あんまり皆さんの出来が悪いから」とわざわざ夏休みに課題を出してくれたおかげです…留年だ留年だって脅すから、そら必死になって課題やりましたさ!
細かい作図法はPDFにまとめておきました。興味のある方はご一読を。創作の助力になれば幸いです。