
無線給電回路シミュレーターを作って
宮崎大学に所属していた時,学部の研究を通してワイヤレス給電回路のシミュレーターを作りました.ワイヤレス給電とは,Qi規格とかあるスマホを置くだけで充電できるあれです.ざっくり言うと,あの機械の回路を設計するためのソフトをつくりました.4年前になるので,忘れる前に書いておこうと思います.
大学院と会社では,まったくシミュレーションソフトを作成することがありません.普通シミュレーションソフトを作るのではなく,買うのが当たり前ですから当然といえば当然です.
ただ,理論がまだ確立していなかった場合,シミュレーションソフトを作成することが研究,開発の第一歩といっても過言ではありません.
ワイヤレス給電回路
ワイヤレス給電は複数種類あり,研究室では低周波数の給電が対象でした.具体的にいうと100MHz程度です.で,なにをシミュレーションしたいのかというと,「回路の抵抗・コンデンサ・コイルの値がどうだと,電力がどのくらい送られるのか.」という問題です.
ということで,まずワイヤレス給電回路ですが,下図のようなものです.
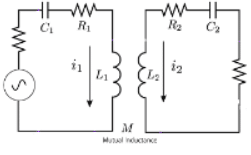
はい,超シンプルです.
工学を勉強したことがある人はお分かりでしょう.ワイヤレス給電回路って,ただの空芯トランスなんですよね.
じゃあ,高校生の電気回路の問題じゃん.となりそうですが,ちょっとそうはいかないんでした.問題は,コイルのインダクタンスを計算する必要があることです.
答えがあるものは少ない
コイルはまけば巻くほどインダクタンスがあがります.さて,何回ほど巻くと,インダクタンスはどのくらいになるでしょう?これを解く必要があります.コイルの物理モデルは以下になります.
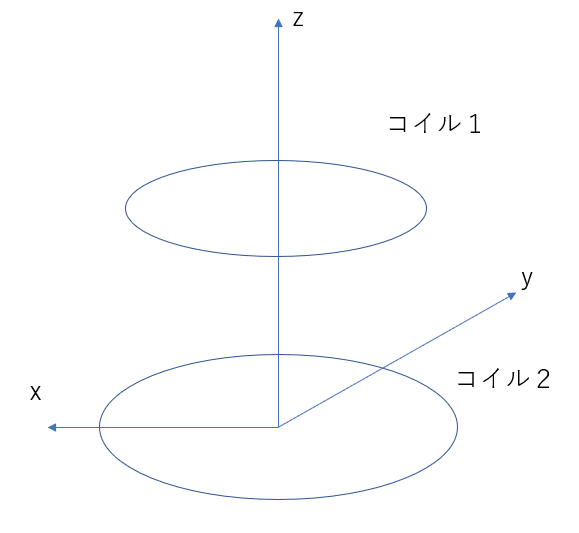
そして,磁束がこちらの式で算出できます.
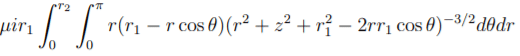
引用:山口和也,高効率・高出力ワイヤレス給電技術へのシステム論的アプローチ
そして,この磁束の式の一般解はありません.
高校や大学では積分を習い,一般解を出せる問題しかなかったと思います.しかし,研究を始めて
え?解ないやん
となる学部4年生がいるかもしれません.僕がそうでした.実は,現実には一般解がある方が珍しいんです.この積分は楕円積分をさらに積分するという無理ゲーイベントが発生します.無理なものは無理です.一般解を出すのは諦めましょう.ということで,学校の勉強でやる理想的な手法ではなく,現実世界で使える方法を使いましょう.数値解析です.
数値解析とは,その名の通り「数値」を実際に代入して近似的に解を得ることです.要は,文字の部分に実際の値を入れて答えを知ろう,ということですね.はい,磁束を算出するという問題はこれでクリアです.
しかし,次の問題はUXです.
計算を早くする
インダクタンスを計算するには上の式を解けば良いです.次に,磁束からコイルの自己インダクタンスと相互インダクタンスを算出します.
コイルは巻けば巻くほどインダクタンスが高くなります.それは上の図,円1つが他の円に対して磁束を増やすからです.1巻き目が2,3,4巻き目に作用する磁束を加算していきます.つまり,巻き数の階乗回の計算が必要です.例えば,6巻きのコイルだと,720回の計算が必要で,2つのコイルを使うので,自己・相互インダクタンスの計算のために2120回積分を解く必要があります.先ほどの数値積分が仮に0.3秒かかるとしたら,インダクタンスを出すだけで10分かかってしまいます.とても待てません.
このように,数値解析を複数回行う必要がある場合は,あらかじめそのデータセットを用意しておくと便利です.幸運なことに,今回の場合だとコイルの半径とコイル間の距離が変数であったので,2次元のデータセットを用意すれば良かったです.とりあえず,半径と距離を0.001ずつ変えていき(※必ず式を無次元化すること!),100万個ほど磁束データを作成し,CSVファイルに保存しました.
さて,このあらかじめ算出した磁束データセットはどうやって使えばいいのでしょう.
結論から言うと,補間関数化して使えばいいのです.
pythonやmatlabなどの数値計算ツールでは離散データから補間関数を作成するモジュールがあるので,それを活用してください.
補間関数だと実際に計算データがない点でも近似した値を瞬時に算出してくれます.都度,計算も必要ないため10分も待たずに一瞬で計算が終わります.
行列計算
みんなが大好きな行列計算についてです.
ワイヤレス給電回路に矩形波を入力したときの電流などの波形は以下になります.

引用:山口和也,高効率・高出力ワイヤレス給電技術へのシステム論的アプローチ
複雑そうですが,意外とpythonで簡単にいけちゃうんですよね~
import numpy as np
import scipy.linalg as la
中略
n = 2000
time = np.linspace(0,T-(T/n),n)
#initializing matrixes for computing easier
A = A / delta
B = B / delta
A_inv = la.inv(A)
AT_exp = la.expm(A*T)
tokusei = la.inv(np.eye(4) - AT_exp)
AT_exp_I = np.eye(4) - AT_exp
A1 = -tokusei.dot(A_inv)
A2 = AT_exp_I*u2
#initializing Xss
Xss = np.zeros((4,1))
#Adding computed value to each list, this process creates datas
for t in time:
if t < T*d:
time2 = t + T*(1-d)
A3 = (la.expm(A*time2) - la.expm(A*t) + AT_exp_I)*u
A3 = A3 + A2
Xss1 = A1.dot(A3).dot(B)
Xss = np.hstack((Xss,Xss1))
if T*d <= t and t < T:
time2_2 = t - T*d
A3 = (la.expm(A*time2) - la.expm(A*t))*u
A3 = A3 + A2
Xss2 = A1.dot(A3).dot(B)
Xss = np.hstack((Xss,Xss2))pythonはfor文が遅いので出来るだけ中の記述を減らすようにします.注目すべきはexponentialの行列を簡単に計算できるところです.これには驚きました.
最後に,Xss(t)の中の電流を積分して,電力を得ます.これには数値積分が必要なのでscipyモジュールのintegrate.rombを使いました.ロンバーグ積分ですね.これで回路素子から電力計算できたよ,めでたしめでたし
UIを作る
各機能を持ったプログラムを汎化関数化し,モジュールとしてパッケージングすれば完了です.それが研究室に配属されて2か月後の6月に完了しました.完了報告すると先輩がボソッと言いました.
「UIあったら便利だよね~」
便利ですね~楽でしょうね~
ということで,UIを作りました.数値解析をしやすいことを理由にpythonを使っていたのですが,pythonでUIは聞いたことがない...
しかし,ありました,Kivyというものが.参考はこちら
で,あんにゃこんにゃしてできたソフトが下になります.


回路の要素を入力して実行ボタンを押すと電力と効率を計算してくれます.画面をスワイプすると回路の波形が表示されます.また,コンデンサや抵抗などの値を変化させていったときの電力変化もシミュレーションできます.そして,なんとBGM機能まで付いています!(というか付けた)
シミュレーションで疲れた時にEuro beatが心を癒してくれます.しかし,卒業論文に載せる時はそこだけ消しました笑 それにしても,UIデザインってむずいですね~.ちなみにアイコンは研究室の女子に3分で作ってもらいました.
このソフトをpyinstallerを使ってexe化し,研究室に配布しました.ただ,pyinstallerはいらないパッケージも含めるので内部エラーが発生し,エラー原因のパッケージを一つずつ消していくのが辛かったです.
ちなみに,この時は入力矩形波をコイル間距離に合わせて変化させ,最大電力を維持する制御手法を卒業論文として提案しました.既にある理論式をシミュレーションできるソフトを作っただけでは大学を卒業できないので,学部生の方は注意しましょう-
以上,シミュレーションソフトを作成するにあたってハマったところや解決方法をつらつら書いていきました.数値解析や積分は意外といろいろなところで役立ったりするので経験してて良かったなと思います.
