
Pythonを用いたクラスター分析【k-meansを用いた不動産価格の推定】
はじめに
仕事に活かすためPythonの勉強を開始し、その中でも特に興味を持ったクラスター分析についてまとめました。
なぜ開始したか
理系出身で新卒からIT業界に身を置きますが、簡単なHTMLやCSSくらいしか書けないことを長らくコンプレックスに感じていたためです。(新卒で営業職になった理系の人なら感じることも多いはず。。。)
なぜPythonを勉強したか
一言にまとめると「データサイエンティスト」という肩書きに憧れたからです。求人を見ていてるとやけにデータサイエンティストの給料が高く、日系大手の会社でもデータサイエンティストの新卒には高めの給料を出すというニュースなども散見され、すごいニーズ高いと感じたからです。
ただ、「Pythonを扱える≠データサイエンティスト」です。でータサイエンティストとは『さまざまな意思決定の局面において、データにもとづいて合理的な判断を行えるように意思決定者をサポートする職務またはそれを行う人』です。データの生み出し方、整理方法などにPythonやRという言語を用いいます。なので、データサイエンティストになるための必要条件だと考え、勉強を開始しました。
本noteの概要
読んで欲しい人
Python初心者の人
データサイエンティストに興味のある人
noteに書くこと
機械学習について
クラスター分析について
Pythonを用いたクラスター分析を事例をもとに紹介
実行環境
Google Colaboratoory
機械学習とクラスター分析について
機械学習とは
機械学習には大きく3種類あります。
ざっくり解説します。前提として、ここで述べる教師とは「データに付随する正解ラベル」を指します。
教師あり学習
学習したモデルから、新しいデータがどのように分類されるのかを予想し、判別できるようにする仕組み。
教師なし学習
与えられたデータからコンピュータ自身が類似性や規則性を見いだして、モデルを学習する仕組み。そのため、正解・不正解が存在しないのが特徴。
強化学習
エージェント(ロボットなど)の動作やシミュレーションを通じ、自動的に「良い」評価になるような動き方を選択できるようにする学習。
例:AIが囲碁の対戦プログラムで人間のプロを破った事例
クラスター分析(クラスタリング)とは?
今回は教師なし学習の中の代表格であるクラスター分析を用います。
クラスター分析の一例として「k-means法」を紹介します。k-meansは以下のステップにより学習を行います。
1. ランダムな位置にクラスタの重心(中心点、例では星と三角)を定める
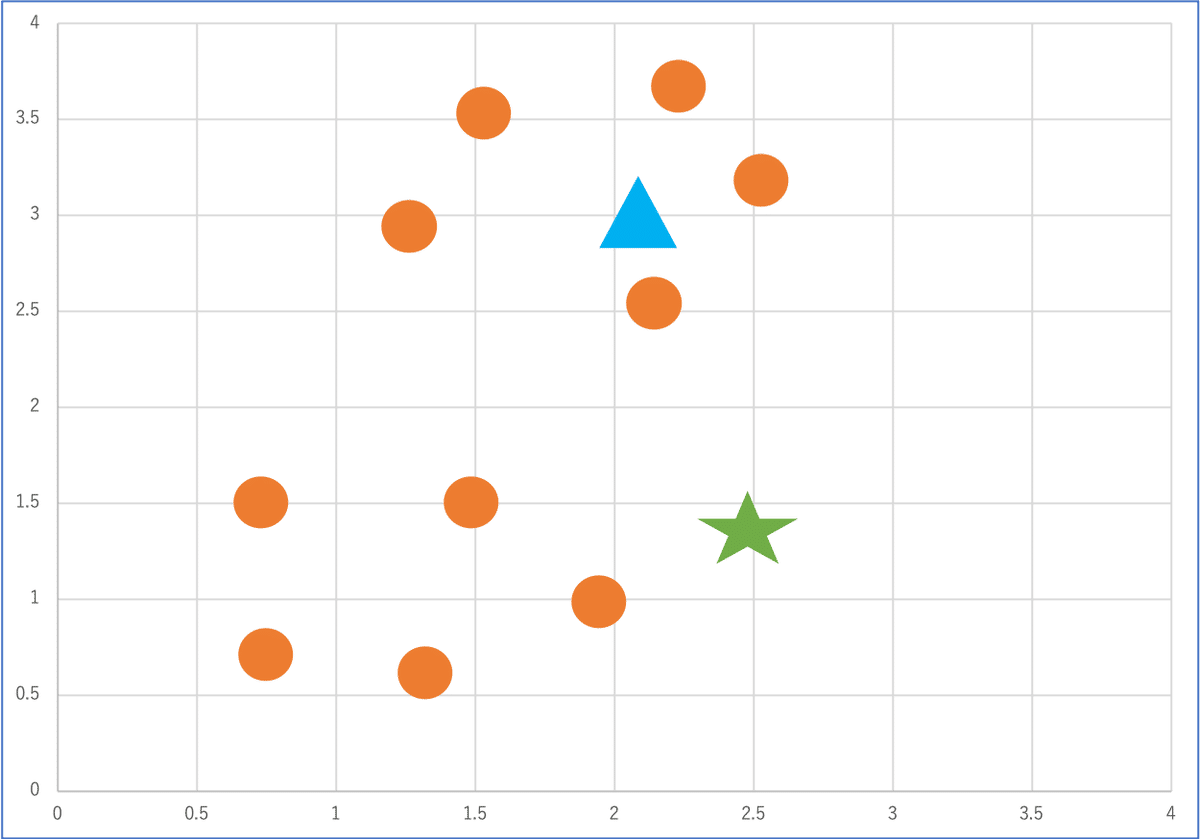
2. それぞれのクラスタの重心と各点の距離を計算
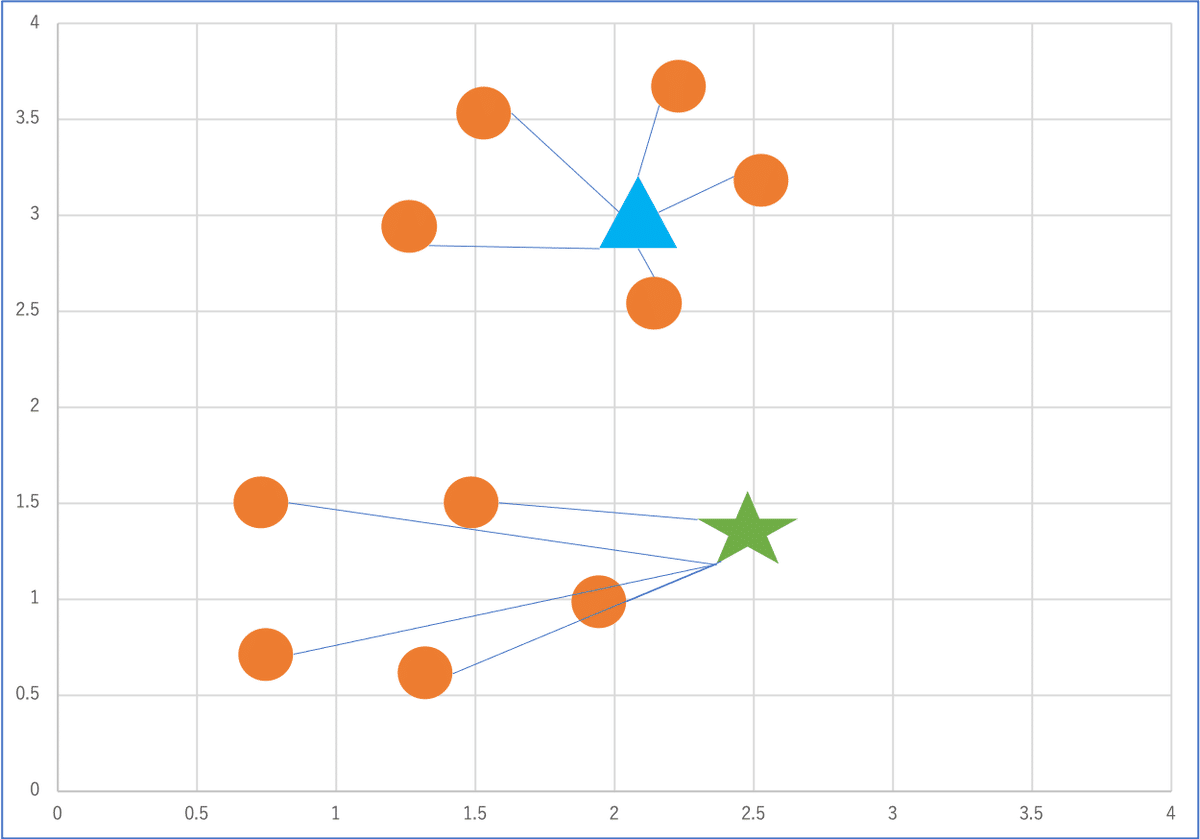
3. 各点を一番近いクラスタに割り当てる
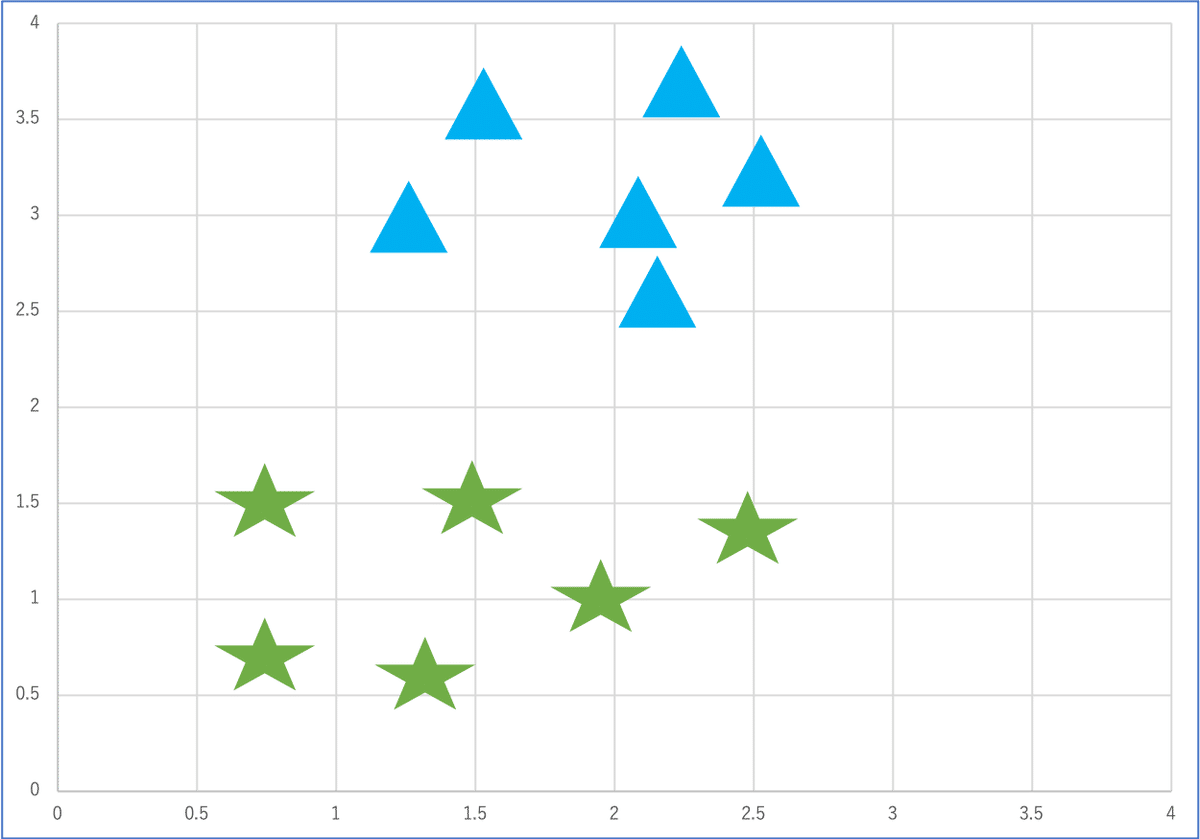
4. 2と3を繰り返し、設定した回数繰り返すか、クラスタの変更がなくなったら終了
クラスター分析の実務での利用例
アパレル店舗
顧客アンケートの結果から、顧客のクラスターを作成し、顧客ニーズに合った商品の陳列
ECサイト
購買データをもとに行動特性をクラスター化する。例えば、「アクセス回数」「アクセス頻度」「利用額」などを分類の基準にして、クラスター化できます。
メールマーケティング
同じ顧客群に複数回に渡り、違った訴求の原稿を送る。顧客の属性と訴求内容を掛け合わせクラスター分析を行い、任意の訴求内容と効果の高い属性を分析する。
実際にやってみる
1.データの取得
ボストンの住宅価格データセット( boston_housing)を取得します。
#データの取得
from sklearn import datasets
import pandas as pd
boston = datasets.load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['MEDV'] = boston.target
print(boston_df)
boston_df.head()
2.データを限定
住宅価格データセットから「CRIM」,「CHAS」,「INDUS」,「DIS 」,「RAD 」,「MEDV」のみに絞ります。選定理由は住宅価格に影響を及ぼしそうであるが、どの程度の影響を与えるか分かりにくいと主観的に感じた項目です。
〈各項目が指すもの〉
CRIM: 町別の「犯罪率」
CHAS : チャールズ川に接しているかどうか (0 : 接していない、1 : 接している)
INDUS : 町ごとの非小売業の割合
DIS : 5つあるボストン雇用センターまでの加重距離
RAD : 主要高速道路へのアクセス性
MEDV : 住宅価格の中央値
#データを限定
columns = ['CRIM','INDUS','CHAS','DIS','RAD','MEDV']
df = df[columns]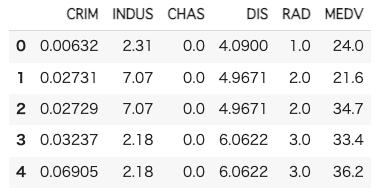
3.欠損値の確認と処理
データには虫食いがあることがよくあります。そのためデータセットを扱う時は基本的に欠損地の確認を行います。isnullとsumを組み合わせて、欠損値を確認します
#欠損値の確認
df.isnull().sum()
各項目の右にある数字が0になっているので、全ての項目において欠損値がないことが分かります。
4.データの標準化
k-meansではデータの大小が影響してしまうため、標準化を実施する必要があります。例えば、ある変数Aと変数Bの値に10倍の差があれば、クラスタリングの結果がその変数に引っ張られてしまいます。sklearnのStandardScalerを使うことで、数値の標準化を行うことができます。
#データの標準化
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
df_sc = sc.fit_transform(df)
df_sc = pd.DataFrame(df_sc, columns=df.columns)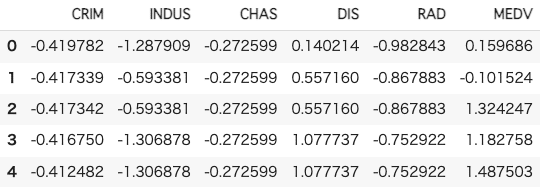
5.クラスタリングの実行
前処理が完了したので、k-meansのクラスタリングを行います。sklearnからKMeansをインポートし、モデルを作成します。n_clustersは分割するクラスタ数です
#クラスタリングを実行
from sklearn.cluster import KMeans
model = KMeans(n_clusters=4, random_state=1)
model.fit(df_sc)上でモデルの作成、適応ができました。labels_を利用してクラスタ番号を取得します。
#クラスタ番号の取得
cluster = model.labels_
クラスタ番号の取得が完了したので、DataFrameの新しいカラムとして、クラスタ番号を追加します。
#クラスタ番号の追加
df['cluster'] = cluster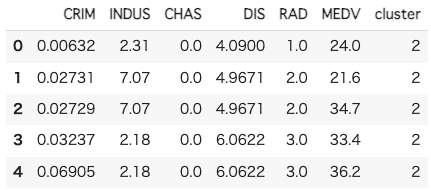
6.クラスタリングの結果を確認
クラスタリングで、「0-3」までのクラスタに分割しました。読み込ませたデータの平均値を、下記コードでクラスタごとに確認することができます。
#クラスタリングの結果を確認
df.groupby('cluster').mean().style.bar(axis=0)
それぞれに傾向が見えてきました。さらに視覚的に分かりやすくするために、この結果を棒グラフに反映します。
#クラスタリングの結果を棒グラフに反映
import matplotlib.pyplot as plt
import seaborn as sb
fig, axes = plt.subplots(2,3, figsize=(14, 6))
sb.barplot(ax=axes[0,0], data=df, x='cluster', y='MEDV')
sb.barplot(ax=axes[0,1], data=df, x='cluster', y='CRIM')
sb.barplot(ax=axes[0,2], data=df, x='cluster', y='CHAS')
sb.barplot(ax=axes[1,0], data=df, x='cluster', y='INDUS')
sb.barplot(ax=axes[1,1], data=df, x='cluster', y='RAD')
sb.barplot(ax=axes[1,2], data=df, x='cluster', y='MEDV')
この棒グラフより、下記のような考察を行うことが可能です。
クラスタ0
最も住宅価格の中央値が高い
川に接している家は高い傾向にある
高速道路へのアクセスのしやすさは高すぎることもなく、低すぎることもなくなので、静かな高級寄りの住宅地だと想定される
クラスタ1
最も住宅価格の中央値が低い
犯罪率の高さから街の治安が悪く、住宅価格が低いと想定される
非小売業の割合が高く、肉体労働や工場など、比較的給料が安めな働き口が多いと想定される
高速道路へのアクセスが悪いため、都会から離れた地方の町であるため価格が低いと考えられる
クラスタ2
2番目に住宅価格の中央値が高い
雇用センターまでの距離が近く、小売業の割合も少ないため、一定の求人と働き口があり、そこそこの世帯収入がある家庭が多いと思われる
クラスタ3
3番目に住宅価格の中央値が高い
際立った傾向は無いが、非小売業の割合が高めであり、クラスタ1と同様に比較的低賃金の仕事が多い可能性がある
7.主成分分析でグラフ化する
今回は特徴値が6つなので、それぞれグラフで可視化しました。しかし、特徴量が増え、より複雑なデータの場合は主成分分析による可視化を行宇野が一般的です。散布図を作成し、視覚的にクラスタリングを確認します。まず、標準化したデータフレームにクラスタ番号を付与します。
#標準化したデータフレームにクラスタ番号の追加
df_sc['cluster'] = cluster続けてPCAをインポートします。n_componentsは必要な主成分を指定することができ、二次元の散布図を作成するために"2"を指定します
#主成分を指定
from sklearn.decomposition import PCA
pca = PCA(n_components=2, random_state=1)
pca.fit(df_sc)
feature = pca.transform(df_sc)
上記で作成したデータを散布図で可視化します。
# データを散布図で可視化
import matplotlib.pyplot as plt
plt.figure(figsize=(6, 6))
plt.scatter(feature[:, 0], feature[:, 1], alpha=0.8, c=cluster)
plt.xlabel('principal component 1')
plt.ylabel('principal component 2')
plt.show()
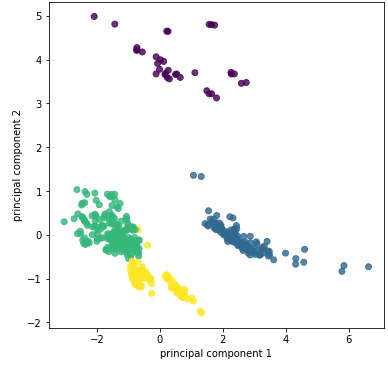
散布図より綺麗に4分割できていることが分かります。
〈番外編〉全データを用いたクラスタリングと散布図
今回は考察をしやすいように「2.データを限定」で特徴値を限定しましたが、限定せずに今回と同じ流れでクラスタリングをした時の散布図は下記のようになります。
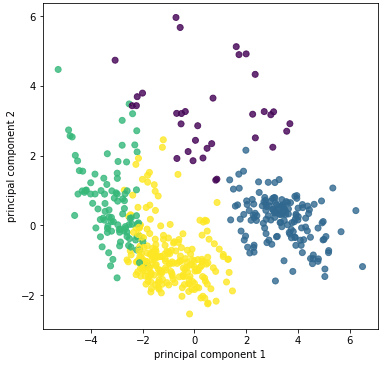
概ね配置は一緒ですが、それぞれの分布の集合具合は広がっています。考慮するべき特徴量が増えることで、クラスタリングを目視でやることは非常に難解になることが分かります。
また、分析をする上で、事前に「仮説」を立てることが何より大切です。今回で言えば、例えば、『「CRIM(町別の犯罪率)」が高い→住宅価格が低い』などです。
仮説も無しにクラスタリングを行なっても、出てきた結果に翻弄され、本来欲しかった結論を見出せないケースも多々あります。
この部分は実践あるのみなので、ぜひ経験を積んでください。
まとめ
k-meansを利用したクラスタリングをPythonで実装しました。数値情報のデータセットであれば汎用的な方法なので、ぜひやってみてください!
