
数の神秘 vol.1完全数について調べてみた。
ちょっと調べていた数の公式のからみで、上のサイトで「完全数」という言葉の響きが気になったので触れてみました。
完全数と推論に至るまで。
完全数に聞きなじみがないとは思いますが、
どうやら、ピタゴラスが命名して、ユークリッドが最初の法則を発見して、オイラーが挑戦した結構有名な数のことのようです。そうそうたる顔ぶれですね。
ピタゴラスは有名ですが、かつて紀元前6世紀、ピタゴラス教団の教祖として数論や幾何学を哲学としていました。数学的対象の存在論的地位を研究したプラトンも、論理学や無限に関する諸問題を研究したアリストテレスも同様です。11世紀以降ではキリスト教の神学者によってスコラ学という論理的な哲学解釈ということもなされました。
数論はロマンだといいますが、発端は哲学だったんです。
完全数とは、 「真の約数の和が自分自身になる数」のことだそうです。
例えば、6 の約数は 1、2、3、6 の四つですが、「真の約数」 とは自分自身より小さな約数ですので、1、2、3 の三つです。 これを全て足し合わせると 6 に戻ります。 したがって 6 は完全数です。
完全数は、いまだ、無限個あるかどうかは確認されていないようです。
これも数論のロマンですね。
本題ですが、既知の完全数を眺めてみて法則性があることに気づきます。
完全数(かんぜんすう、英: perfect number)とは、自分自身が自分自身を除く正の約数の和に等しくなる自然数のことである。完全数の最初の4個は 6 (= 1 + 2 + 3)、28 (= 1 + 2 + 4 + 7 + 14)、496 (= 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248)、8128 (= 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1016 + 2032 + 4064) である。
哲学になる完全数なので法則性があることは当たり前ですが、気付いたことを書き出してみます。
6: 1+[2]+4+(-1)
28: 1+2+[4]+8+16+(-1)+(-2)
496: 1+2+4+8+[16]+32+64+128+256+(-1)+(-2)+(-4)+(-8)
8128: 1+2+4+8+16+32+[64]+128+256+512+1024+2048+4096+(-1)+(-2)+(-4)+(-8)+(-16)+(-32)累乗の和がポイントのようです。
完全数がn個の数の和とした場合、
累乗の和である2^n - 1から数列の中央値(中央値は含まない)※(n-1)/2番目の数値までの累乗の和を引いたものであると推察できます。
完全数の要件のひとつとして以下を挙げてみます。
n個の数値で以下の公式で導き出せる数となる。
※整数の中央値を必要とするためnは奇数とする。
完全数がn個の数の和とした場合に、
完全数の候補となる数の集まりをP(n)としたとき、以下の公式で表す。
P(n) = (2^n - 1)-(2^( (n - 1) / 2 ) - 1)
Excel:=(pow(2,$C$1)-1)-(pow(2,int(($C$1-1)/2))-1)
※$C$1はnを表す。既知の完全数の一部
6, 28, 496, 8128, 33550336, 8589869056, 137438691328, 2305843008139952128, 2658455991569831744654692615953842176, 191561942608236107294793378084303638130997321548169216
実際に計算して書き出してみましょう。
n:1 ⇒ 1
n:3 ⇒ 6 ※既知の完全数
n:5 ⇒ 28 ※既知の完全数
n:7 ⇒ 120
n:9 ⇒ 496 ※既知の完全数
n:11⇒ 2016
n:13⇒ 8128 ※既知の完全数
n:15⇒ 32640
n:17⇒ 130816
n:19⇒ 523776
n:21⇒ 2096128
n:23⇒ 8386560
n:25⇒ 33550336 ※既知の完全数
n:27⇒ 134209536
n:29⇒ 536854528
n:31⇒ 2147450880
n:33⇒ 8589869056 ※既知の完全数
n:35⇒ 34359607296
n:37⇒ 137438691328 ※既知の完全数
n: 3,5,9,13,25,33,37完全数なのは、n: 3,5,9,13,25,33,37
どうやら分布があるみたい。
目につくのはnが
3^a: 3,9
5^a: 5,25
13、37も素数なので
たぶん
13^a: 13,169…
37^a: 37,1369…
も完全数だと思う。
この時点で「完全数は無限個存在するんじゃないかな」と思いました。
「中心つき多角数」の一覧を眺めてみて。
33は、3×11なので素数じゃない。
3,5,13,37は素数
で特徴は、
13:
左切り捨て可能素数 ピタゴラス素数 幸運数 メルセンヌ素数の乗数 プロス数 フィボナッチ数 13のべき乗数 ウラム数 十三角数 不足数 置換可能素数 陳素数 中心つき十二角数 トリボナッチ数 中心つき四角数 エマープ数 ハッピー数
37:
幸運数 不足数 右切り捨て可能素数 キュバン素数 中心つき十二角数 陳素数 置換可能素数 エマープ数 中心つき六角数 左切り捨て可能素数 ピタゴラス素数
13,37で共通しているのは、ピタゴラス素数、幸運数、陳素数、エマープ数、置換可能素数、中心つき十二角数。
このなかで、中心つき十二角数(中心つき多角数)に注目。
このWikiの説明を見ると、
「中心つき四角数」に「5」「13」「25」が存在する。
「中心つき八角数」に「9」「25」が存在する。
「中心つき十二角数」に「13」「37」が存在する。
中心つき多角数(ちゅうしんつきたかくすう、英: centered polygonal number)とは、正多角形の形に点を中心から順に並べたときにそこに含まれる点の総数にあたる自然数である。
主な中心つき多角数は以下の通りである。
中心つき三角数:1, 4, 10, 19, 31, …( A005448)
中心つき四角数:1, 5, 13, 25, 41, …( A001844)
中心つき五角数:1, 6, 16, 31, 51, …( A005891)
中心つき六角数:1, 7, 19, 37, 61, …( A003215)
中心つき七角数:1, 8, 22, 43, 71, …( A069099)
中心つき八角数:1, 9, 25, 49, 81, …( A016754)
中心つき九角数:1, 10, 28, 55, 91, …( A060544)
中心つき十角数:1, 11, 31, 61, 101, …( A062786)
また、中心つき九角数は 6 以外の完全数を含み、中心つき八角数は奇数番目の平方数であり、中心つき十二角数は六芒星数と一致する。
なので、nが41、49、73の時に完全数であれば、「中心つき四角数」「中心つき八角数」「中心つき十二角数」であれば完全数であると推測できる。
便宜上、wiki上の公式のnをmと表記する。
中心つき四角数 : 2m^2-2m+1 :1,5,13,25,41…
中心つき八角数 : 4m^2-4m+1 :1,9,25,49,81…
中心つき十二角数: 6m^2-6m+1 :1,13,37,73,121…
中心つき二十四角数: 12m^2-12m+1 :1,25,73,145,241…
完全数なのは、n: 3,5,9,13,25,33,37だったので
それぞれ1を引いた中心つきN角数にあたる、
N: 2,4,8,12,24,32,36
中心つきの、二角数(存在しないけど多分、m^2-m+1)、四角数、八角数、十二角数、二十四数、三十二数、三十六数….
で算出されたnが完全数のもととなるnであると思う。
それぞれ無限にあるので、「完全数は無限個存在するんじゃないかな」とも思える。
あと、こういう「中心つき4nの多角形」という観点で見ると元素の周期表を思い出しますね。
ということで推論をまとめると以下の通り
既知の完全数のパターン
6: 1+[2]+4+(-1)
28: 1+2+[4]+8+16+(-1)+(-2)
496: 1+2+4+8+[16]+32+64+128+256+(-1)+(-2)+(-4)+(-8)
8128: 1+2+4+8+16+32+[64]+128+256+512+1024+2048+4096+(-1)+(-2)+(-4)+(-8)+(-16)+(-32)
より、累乗の和である2^n - 1から数列の中央値※(n-1)/2番目の数値まで(中央値は含まない)の累乗の和
を引いたものであると推察できる。
よって完全数の要件のひとつはn個の数値で以下の公式で導き出せる数となる。
※整数の中央値を必要とするためnは奇数とする。
★ (2^n - 1)-(2^( (n - 1) / 2 ) - 1)
Excel:=(pow(2,$C$1)-1)-(pow(2,int(($C$1-1)/2))-1)
※$C$1はnを表す。
このnによって算出した値の一部は以下の通り:
n:1 ⇒ 1
n:3 ⇒ 6 ※既知の完全数
n:5 ⇒ 28 ※既知の完全数
n:7 ⇒ 120
n:9 ⇒ 496 ※既知の完全数
n:11⇒ 2016
n:13⇒ 8128 ※既知の完全数
n:15⇒ 32640
n:17⇒ 130816
n:19⇒ 523776
n:21⇒ 2096128
n:23⇒ 8386560
n:25⇒ 33550336 ※既知の完全数
n:27⇒ 134209536
n:29⇒ 536854528
n:31⇒ 2147450880
n:33⇒ 8589869056 ※既知の完全数
n:35⇒ 34359607296
n:37⇒ 137438691328 ※既知の完全数
完全数であるnは以下の通りで、既知の
n: 3,5,9,13,25,33,37
既知の完全数の一部はすべて網羅している
3:6,
5:28,
8:496,
13:8128,
25:33550336,
33:8589869056,
37:137438691328,
??:2305843008139952128,
??:2658455991569831744654692615953842176,
??:191561942608236107294793378084303638130997321548169216
既知の完全数はnが37までですが、全て網羅している。
完全数に対応するnは、「中心つき多角数」のによって導くことができると推測する。
nのとき、「中心つきN角数」※N = n - 1 の公式によって導き出されるnの候補の集合 F(n) は以下の通り
★ F(n) = ( (n - 1) / 2)m^2 - ( (n - 1) / 2)m + 1
n「3」のとき「中心つき2角数」の公式の結果は以下の通り
F(3) = m^2 - m + 1
= {m:1,2,3,4,5,F(3):1,3,7,13,21}
※3以外は完全数にならない。⇒ F(3)は対象外。
なので、n:1~4の場合は完全数にならなそうなので、
★ n < 5 のF(n)は除外対象、ただし m = 2 の場合はその限りでない。
としてみる。
あと、nは奇数で、既存の完全数の分布を眺めてみると、
どうやら次のNまで4以上空くようです。それに4の倍数 に分布しているようですね。
★ q={1,2,3,4,5...}とした場合 N = 4q に分布する。
n「5」のとき「中心つき4角数」の公式の結果は以下の通り
F(5) = 2m^2 - 2m + 1
= {m:1,2,3,4,5, F(5):1,5,13,41,61}
新しく13,41,61が導き出されたので
同様に
n「13」のとき「中心つき12角数」の公式の結果は以下の通り
F(13) = 6m^2 - 6m + 1
= {m:1,2,3,4,5, F(13):1,13,37,73,121}
n「9」のとき「中心つき8角数」の公式の結果は以下の通り
F(9) = 4m^2 - 4m + 1
= {m:1,2,3,4,5, F(9):1,9,25,49,81}
このように、(n - 1) [n >= 5] : 4,8,12,24,32,36
の「中心つき(n-1)角数」で導出されたF(n)によって完全数 P の集合を
P(F(n)) = (2^F(n) - 1)-(2^( (F(n) - 1) / 2 ) - 1)
[n >= 5]
とし推測する。
ExcelやGoogleのスプレッドシートだと巨大な整数を扱えないので、推論の確認にはアプリを作るか、専門のPCがいるのかもしれません。
検証
巨大な数を計算できそうなサイトがありましたので検証してみます。
現在51番目の完全数が判明しているそうですが、約4900万桁の数値だそうなので、さすがに検証をここで行うのは無理そうです。
ですので、nが37以降で想定した完全数を、既知の完全数で当てはまるかを確認します。

計算式が合っているか試してみます。
n=37 : P(37)=137438691328
公式はあっていそうです。
では、想定している「中心つき多角形」のnの値を試してみます。
100未満のnを出してみたいと思います。
中心つき4角形 :{m:2,3,4,5..10 F(3) : 5,13,25,41,61,85,113,145,181}
中心つき8角形 :{m:2,3,4,5..8 F(9) : 9,25,49,81,121,169,225}
中心つき12角形:{m:2,3,4,5..7 F(13): 13,37,73,121,181,253}
中心つき24角形:{m:2,3,4,5 F(25): 25,73,145,241}
中心つき32角形:{m:2,3,4,5 F(33): 33,97,193,321}
中心つき36角形:{m:2,3,4, F(37): 37,109,217}とりあえず、上記多角形で、確認済みの38未満の数を除いた以下の数をnとして確認します。
TestN: {41, 49, 61, 73, 81, 85, 97}
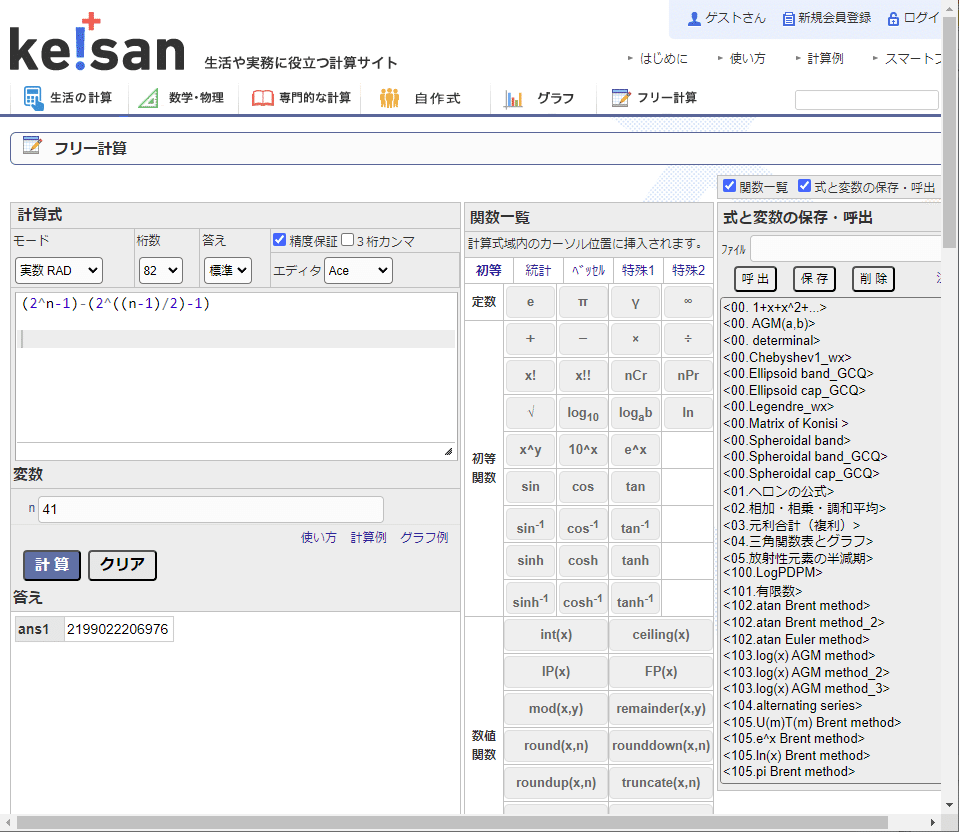
確認結果
n=41: P(41)=2199022206976
n=49: P(49)=562949936644096
n=61: P(61)=2305843008139952128
n=73: P(73)=9444732965670570950656
n=81: P(81)=2417851639228158837784576
n=85: P(85)=38685626227663735544086528
n=97: P(97)=158456325028528393712111190016上記確認では、n=61のみが既知の完全数でした。
残念ながら、他の数は既知の完全数にはありませんでした。
しかし、一つ見つかったので、次の37桁の完全数「2658455991569831744654692615953842176」
にあたるnを探してみます。
n=97の158456325028528393712111190016が30桁なので、7桁増えますね。
2の20乗が1048576なので、n=121あたりでしょうか。

n=121でいけました。
では
191561942608236107294793378084303638130997321548169216
はどうでしょうか。
54桁なので、54-37=17桁増えます。
log2 10^17 = 56….
121+56=178
次は181あたりではないでしょうか。
ちなみにn=61が完全数だったので以下を候補に追加します。
中心つき60角形:{m:2,3,4, F(61): 61,181,361}n=181で確認すると。。。
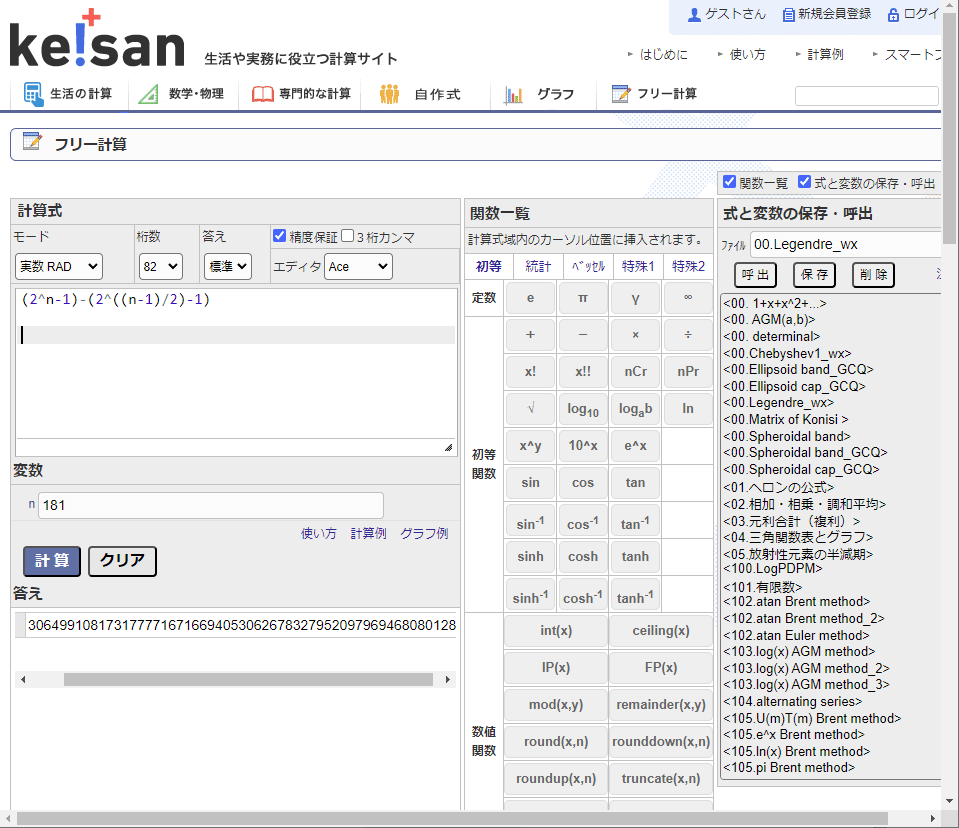
えー違ったし。1桁多い。でも周辺には169くらいしかないから桁合わない。
探してみる。
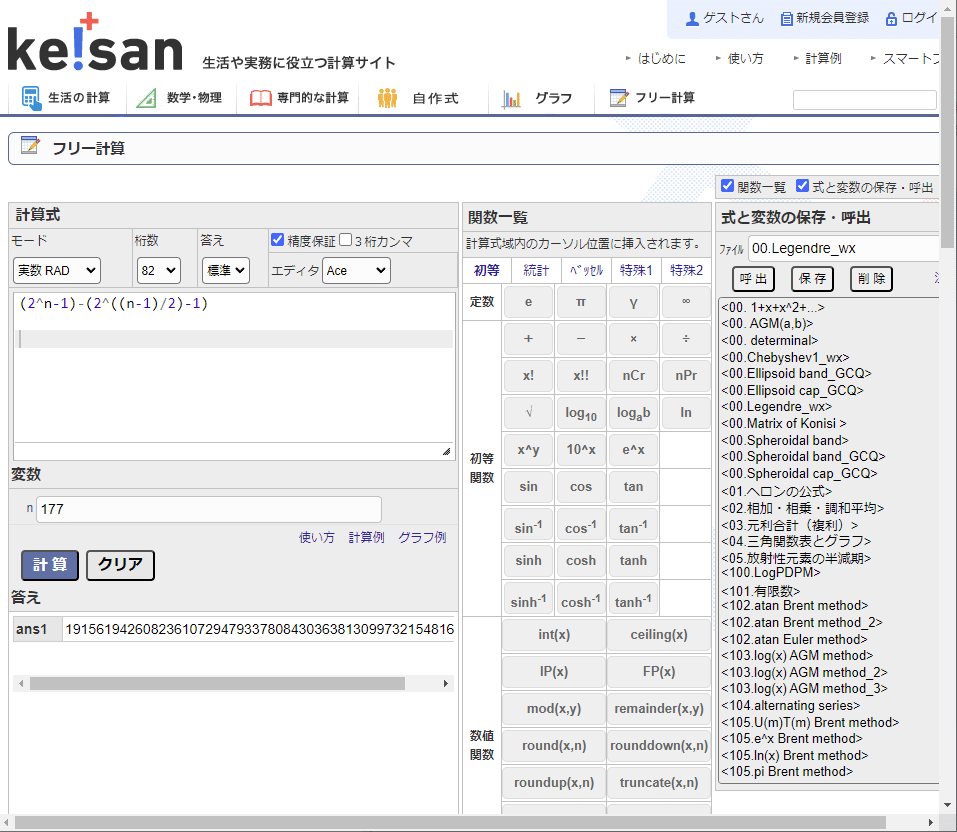
あったけど一覧にないnの数字だった。
177は3×59の数値
これは33と同じようなパターンのような気がします。
n=13とn=61がn=完全数なので、
12と60に関係ありそうですね。
もしくは16と64でしょうか。
短絡的ですが2^(2n)-5として
2^4-5と2^6-5なので2^8-5を試してみましょうか。
2^8-5=256-5=251
251×3=753なので
n=753で試してみます。

残念ながら桁あふれです。226桁は出力できないと確認できません。
既知の完全数の一覧表があったので、それをもとに、確認できそうな完全数を確認していきます。
n=213:P(213)=13164036458569648337239753460458722910223472318386943117783728128
n=253:P(253)=14474011154664524427946373126085988481573677491474835889066354349131199152128n=213とn=253が見つかりました。
しかし、n=253は「中心つき12角数」ですが、213は見当たりません。
33と177と213に共通していることって何でしょうか。
いずれも3の倍数で{3×11, 3×59, 3×71}となります。
12と60と72に関係ありそうですね。
12の倍数に1を引いた値ということは共通しています。
ということは言い換えると
33と177と213は36の倍数に3を引いた値です。
しかし、n=69、n=105、n=141は完全数ではないみたいです。
n=69: P(69)=590295810341525782528
n=105:P(105)=40564819207303336344294875201536
n=141:P(141)=2787593149816327892690784192460327776944128そういえば序盤で、n=13^a{ 13,169…}、が完全数ではないかと推測していましたが、n=169は残念ながら完全数ではありませんでした。
あと、「中心つき多角数」で
TestNで完全数から除外された数値 {41, 49, 73, 81, 85, 97}にも法則があるかもしれません。
でも除外が増えてくると、完全数が無限に存在するという可能性が減っちゃいます。
こんな調子で、他の完全数も確認できそうですが、桁数の問題でこれ以上は手軽に確認できなさそうです。今回はここまでです。
感想。
次の日の朝、完全数のWikiをちゃんと読んでみると、こんなことが書いてありました。
偶数の完全数の性質
偶数の完全数は全て奇数番目の三角数でもあるので、知られている完全数は全て六角数でもある。六角数の列は
1, 6, 15, 28, 45, 66, 91, 120, 153, 190, 231, 276, 325, 378, 435, 496, 561, …(オンライン整数列大辞典の数列 A000384)
n 番目の六角数は n(2n − 1) なので、偶数の六角数は 2n(4n − 1) で表される。偶数の六角数の列は
6, 28, 66, 120, 190, 276, 378, 496, 630, 780, 946, …(オンライン整数列大辞典の数列 A014635)
やっぱり、歴史が長いだけあって似たようなことはすでに発見されていました。
ただ、自分で発想した推論で探求することが、こういった数論の面白みだと思いますし、新しい発見はこういった活力から生まれてくるものだとも思います。
数論のロマンを体験できましたし。充実した一日でした。
最後に約数と約数の総計を確認できるサイトがありましたので紹介しておきます。ただ、16桁までしか確認できません。
よろしければサポートお願いします! いただいたサポートはクリエイターとしての活動費に使わせていただきます!
