
3.三角測量(3次元)1/2
はじめに
前回は2次元での三角測量の計算を紹介しました。今回からは、それを3次元に拡張する方法を説明していきます。2次元に比べて導出過程が長いので2回に分けて説明したいと思います。
モデル化
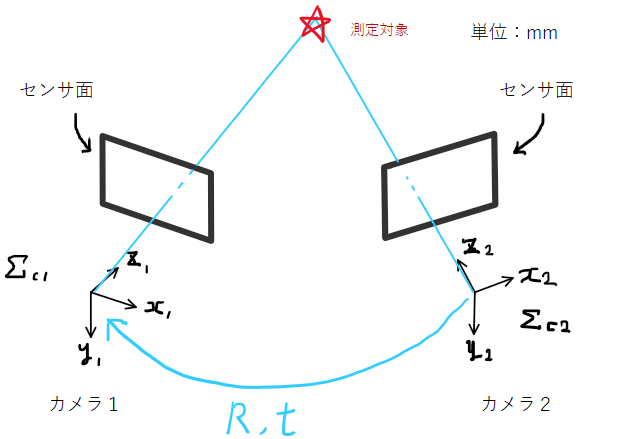
まず計算を始める前にステレオ方式のモデルについて説明します。下図の様にカメラが2つ離れた位置(相対的な位置関係(回転行列R,並進行列t)は既知とする)に設置されている状態を考えます。ここでは2台ともカメラとして説明しますが、一方がプロジェクタでも考え方は同じです。また、カメラで撮影した画像は歪がないものとして考えます(いわゆるピンホールカメラモデルと呼ばれるモデルで、前処理で歪が除去されたものとして考えます)。普通、カメラ主点に対してセンサ面は後方にありますが、反転して扱い難いので便宜上主点の前に置いて考えます。カメラ主点を原点とた座標系をここではカメラ座標系と呼ぶこととします。
上のモデルは単位がmmの世界で定義されています。一方カメラから得られる情報は輝度値と画素座標のみですので、mmとpixとの対応関係を定義できるようセンサ面にも座標系(ここではセンサ座標系と呼ぶことにします)を置きます(下図)。画像データは2次元なのでこの座標系も2次元です。ここで、mmとpixの対応付けができるようピクセルサイズの逆数をη[pix/mm]と定義します(縦横でサイズが違う場合があるので、xとy両方定義しておきます)。ηを定義することで、焦点距離f(主点からセンサ面までの距離)をピクセル数で表現することができるようになります。
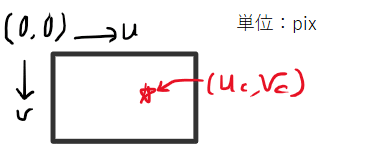
(センサ上で見える対象の座標をuc,vcとしている)
$$
f_x=\eta_xf\\
f_y=\eta_yf\\
(\eta_x[pix/mm],\eta_y[pix/mm])
$$
また、図示していませんがセンサ中心画素座標を下記のように定義しておきます。(カメラ座標原点からセンサ面に垂直に引いた線はセンサ中心を通るものとします)
$$
\text{x方向のセンサ中心座標:}c_x [pix]\\
\text{y方向のセンサ中心座標:}c_y[pix]
$$
カメラ座標系とセンサ座標系の関係
次に、測定対象とセンサ面上の座標との関係を求めます。下の図は、カメラ主点を原点としたときに、座標(Xc,0,Zc)に測定対象があるときのセンサ面上との座標との関係を図で表しています(ここではまだ単位はmmなので注意してください)。
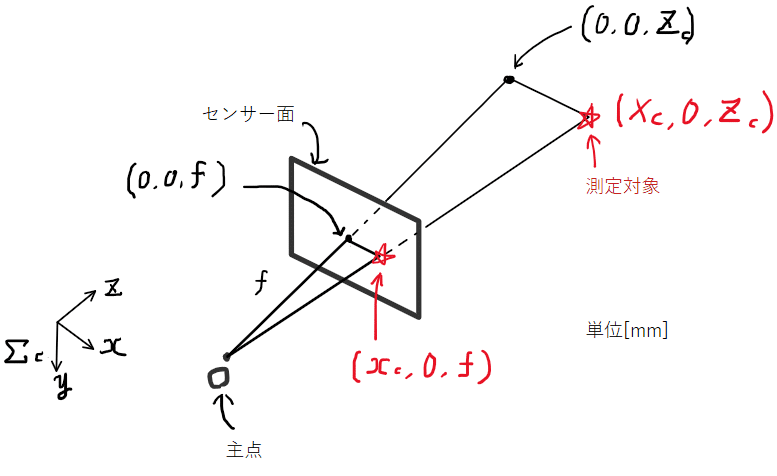
ここで、主点Oと測定対象を結んだ線を引いたときにセンサ面上との交点を(xc,0,f)とします。これが、カメラで見たときに見える対象物の位置で、以下のような関係があります。
$$
\cfrac{x_c}{f}=\cfrac{X_c}{Z_c}\\
\\
左辺に \cfrac{\eta_x}{\eta_x}を掛けると\\
\\
\cfrac{\eta_x x_c}{\eta_x f}=\cfrac{u_c-c_x}{f_x}=\cfrac{X_c}{Z_c} となる\\
\\
同様に\\
\\
\cfrac{\eta_y y_c}{\eta_y f}=\cfrac{v_c-c_y}{f_y}=\cfrac{Y_c}{Z_c} と表せる\\
\\
整理すると\\
\\
$$
$$
\begin{cases}
Z_cu_c=f_xX_c+Z_cc_x \\
Z_cv_c=f_yY_c+Z_cc_y
\end{cases}
$$
とまとめられます。このあと式展開しやすくなるよう行列で表現すると下記のようになります。
$$
Z_c
\begin{pmatrix}
u_c\\
v_c\\
1
\end{pmatrix}
=
\begin{pmatrix}
f_x & 0 & c_x\\
0 & f_y & c_y\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
X_c\\
Y_c\\
Z_c\\
\end{pmatrix}
$$
この式によりカメラ座標系とセンサ座標系を関係付けることができます。また、カメラ内の焦点距離と中心座標でまとめられた行列を内部パラメータと呼ぶこととします。
$$
K_{cam}=
\begin{pmatrix}
f_x & 0 & c_x\\
0 & f_y & c_y\\
0 & 0 & 1
\end{pmatrix}
・・・内部パラメータ
$$
流れだけ見ていると重要そうに思えないかもしれませんが、実世界の座標とカメラセンサ内の座標とを結びつける重要な式です。ただ、求めたいカメラ座標系の変数3つに対し、センサ座標系の変数は2つなので式が不足しています。今のままだと、主点Oとセンサ面上で見た測定対象の画素位置を結んだ線の延長線上のどこかに解があることしか分かりません。
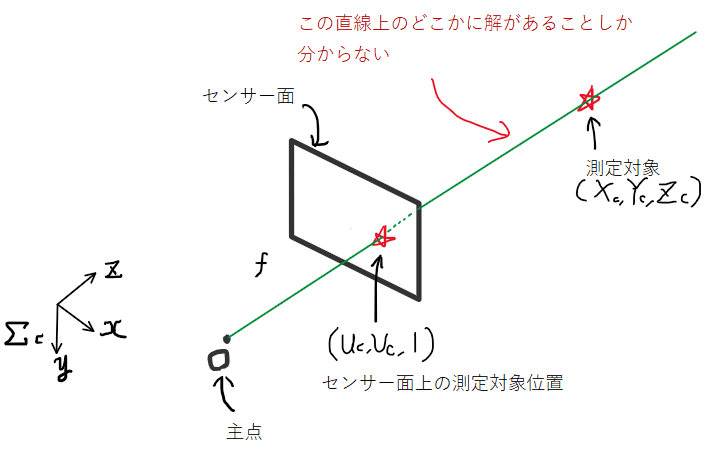
つまり、式が不足しているのでもう一つカメラを増やして式を増やすことで解を求めれば良いのです。今回はここまでとして、次回はもう一つ式を作り連立方程式を解いていきます。
自分がつまづいた点(特にpixとmmとの換算あたり)を、丁寧目に開設したつもりですが如何だったでしょうか。もし分かり難い点や不備があればコメントいただければと思います。引き続きお付き合いの程よろしくお願い致します。
