
メジャースケールは2つあったッ!22平均律スケール編【043】
こんにちは、こんばんわ、ユートピア!
変拍子兄さんのお時間です!
前回の22平均律の話に引き続き、
本日は、スケールの話にすすんでいこうかと思います
◆22平均律のスケールテーブル

スケールを分析するためにこのようなフォーマットを用意しました。
1マス1Step横に広がり、スケールに該当する音がグリッドの中に出現します
22平均律だとそこまで横に広がらないので、スケールの比較用として
活用していきます
22平均律ではε、Λ、βなど音名として見慣れないやつを多用しますが
このフォーマットなら、その意味を深く知らなくても
どういうスケールなのか分かりますし
どの音が派生したのかというのも分かりかなり便利になるでしょう
◆ステップの読み方
スケールの表し方として、多用されるのが

この形式
この形式の利点は、数字ベースで定義されていることから、スケールの情報に解釈の余地はなく、一意的なのがいいですね
ただ、この数字の羅列を見ても慣れてない人はなんなのか全くわからないため
僕の解説ではスケールテーブルに書き起こして比較していくという手法をとっていきます
XenharmonicWikiでScaleの情報は基本的にこの形式です
僕が22平均律の情報源として使っている、このページにもでてきます
これらを読み解いて、22平均律の基本スケールを考えていこう
という試みです
◆4つの基本スケール
基本となる4つのスケールは
①スーパーメジャースケール
②ジャストメジャースケール
③ナチュラルマイナースケール
④サブマイナースケール
ですが、いったん忘れて
鍵盤だけの状態からスケールを考えていきましょう
通常スケールを考える際、純正音程を気にしつつ
幅がバラバラにならないように考慮
という形でスケールを構築していきますが
22平均律では5度が709セントとやや高いため、3倍音系の純正音程を表すのには向いていない平均律となります
そのため今回は純正音程の話をせずに進めていきます
まず、第1候補として考えられるのは白鍵の7音です。
何といっても白鍵ですから
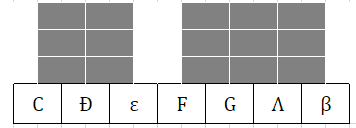
それではこいつの名前は?、となりますが
前回のインターバルの命名より
「スーパーメジャースケール」
と呼ぶことにしましょう
ちなみにXenharmonicWikiではSuperpyth Ionianとなりますが
スーパーパイスの説明が面倒なので割愛します
セントで見ると、思ったより高い印象を与えるものが多いですが
聴いてみると、12平均律のメジャースケールと似た感じがするので
基本として申し分ないですね
スケールのステップは4414441
音程の種類は4Stepと1Stepの2種類、この構造が12平均律メジャーと同じ雰囲気を出しているわけです
ということで、基本スケール①はこいつです
次にE,A,Bが純正音程に近いことから、これらを使った音階を考えていきます
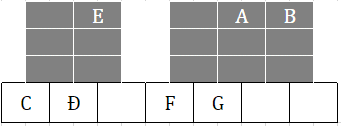
3,6,7度が1Step下がっただけのスケール
旋律にすると、幅の不均等感が目立つため
スーパーメジャーほど使いやすくはないです。
ですが真価を発揮するのは、ハモリで
このスケールをもとにハモリを構築すると、綺麗にハモリます
というわけで基本スケールその②です
3番目、マイナー側を考える必要がありますね
3度で考えると
この位置に来るマイナーが欲しいですね
何なら、これ↓のように6,7度もスーパーマイナーだとなお良い…
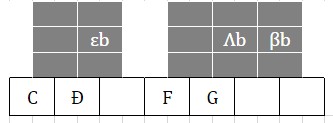
これをWikiで調べてみると、該当するスケールがありました
ナチュラルマイナーと名付けられていました。
このスケールは純正に近い音程をとることから
12平均律のナチュラルマイナーと同様の「ナチュラル」の称号を手にしたようです。
ちなみにジャストマイナーは7thがもう一つ低く7倍音に合わせているようです。
4番目、こうなると最後は
3,6,7度すべてサブマイナーになっているものがいいですね
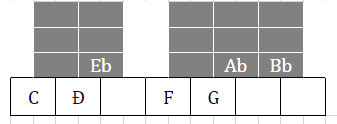
これはスーパーメジャースケールを転回させて
このスケールが完成します
これをサブマイナースケール と呼ぶことにしましょう
(Superpyth Aeorian)
この4つを並べると
3,6,7度が綺麗に間を埋めてくれるのでこの4つのコンビネーションで
ほぼ網羅できます

というわけで、この基本スケールを実際に歌って練習できるように
このような、音源をつくりました。
22平均律シャトルランを作りました。 pic.twitter.com/jn44V1hgM9
— 変拍子兄さん@太鼓受かった (@OrangeTheKeyqa) July 12, 2020
◆アドバンスな6つのスケール
⑤スーパーリディアン
⑥ジャストリディアン
⑦ブライトメジャー
⑧シンメトリックマイナー
⑨ツァルリーノフリジアン
⑩サブフリジアン

基本の4つのスケールを並べると
CとÐの間とFとGの間を使用したスケールがありません
22平均律の22音をすべて使えるようになるには
これらの音程を含んだスケールが必要になります
そのために選ばれた6名がアドバンスドスケールというわけです。
⑤⑥⑦がFを変化させるもの
⑧⑨⑩がÐを変化させるもの ですね
注意点として良く見ると3,6,7度がその都度違うので注意
⑤スーパーメジャー→スーパーリディアン
⑥ジャストメジャー→ジャストリディアン
⑧ナチュラルマイナー→ツァルリーノフリジアン
⑨サブマイナー→サブフリジアン
という風に、元のスケールを1音変えただけのものです。
ただし・・・・。
⑦ブライトメジャー
⑧シンメトリックマイナー
はなんか様子がおかしいです。
ここに少々解説を加えますと
シンメトリックマイナーは、F#/Gbの軸からみて左右対称にできています。
そしてブライトメジャーはこれの転回形というものになります
C#/Ðbが対称軸になってると考えると覚えやすいでしょう
実際には、ハーモニックマイナーを使用したいとか
「転回したらどうなる?」とか、「このパターンも考えられる…」
「そもそも7音である必要はないな」 etc...
と色々考えてしまうと、膨大な数のスケールがでてきますので
ここに提示した10種のスケールでひとまずは十分だろうという感じがします。
◆スケール発展編、MOS属性
さて10個のスケールを把握すれば、
全22音を使用して曲作りができます。
そこからさらにスケールの話を展開させていくわけなので
マニアックなスケール論の入り口となります
ここからは、特に真剣に付き合う必要のない、マニアックなゾーンです
与えられた10個では物足りない、もっとスケールの神髄に踏み込んでいくようなdeepなセオリーが見たいという方のみ
この項をご覧ください
________________________
◆MOSとDiatonic
まずはMOSについて
MOSとはMoment Of Simmetry
2種類のステップで構成されるスケールのことをMOSといいます
12平均律でいえば
メジャースケール→2212221
マイナースケール→2122122 などがMOSと言えます
一方、ハーモニックマイナー→2122132
となり3種類幅がありますからMOSではありません
次にMOSの広いステップをL、狭いステップをSとして
4L2s という風にMOSのパターンを表記することがあります
このようにL sという風に一般化してしまえば
さまざまな平均律に応用できるようになります
例えば12平均律のメインとなるメジャーマイナーが5L2s
L=2Step s=1Step
これを L=4Step s=1Step という風にLとsの比率を変えてあげると
4414441 となり22平均律のスーパーメジャースケールとなります
つまりスーパーメジャースケールと12平均律のメジャースケールは
同じ構造のMOS と言えます
そして5L2sにはdiatonicという名前がついています
これはすなわちスーパーメジャースケール/サブマイナースケールから
コードを生成するとdiatonic chordsと言えますが
ジャストメジャー、ナチュラルマイナーの場合はnon-diatonic chordsと言えます
これはいわゆるノンダイアトニックコード
→「ノン」+「ダイアトニックコード」
とは異なり
「ノン+ダイアトニック」+「コード」 ということを示します
何気なく使っている
「ダイアトニック」って本当はどういう意味なんでしょうね?
ピタゴラス音律の2全音=ディトノスから来てるのは間違いないですが
5L2sという構造=ダイアトニック となっているのは
もう少し深掘りしてみたいところがあります。
◆MOS属性、スーパーパイス・ポーキュパイン
さらにある平均律上で、あるMOSが特定の条件を満たすことで
属性が付与されます。
(純正音程・コンマをなんたら~っていう定義がありますが割愛)
そこで登場するのがスーパーパイスとポーキュパイン
22平均律でもいろんなMOSが作れるわけですが
その中でも特定の条件を満たしたMOSたちに
スーパーパイス、ポーキュパイン
(マジック、ヘッジホッグ、アストロノミー、オーウェル、パジャラなどなど)
という属性が付与されます
今回登場した
スーパーメジャー、サブマイナー、スーパーリディアン、サブフリジアンは4414441の転回のMOS
これらにはスーパーパイスという属性が付与され
シンメトリックマイナーやブライトメジャーが3334333の転回のMOS
これらがポーキュパインという属性が付与されます
これらの属性のことをファミリー というらしいですが
詳しいことはまだ僕も分かりませんので
色々調べて、超マニアック編として後々語ることにしましょう。
◆
語りすぎてキリがない感じもしますし、
スケール論、こういう広がり方をしているぞ!ってだけ知ってもらえれば今回はOKです
まあ、今後スケールの上位グループを考える時に必要不可欠な存在になってきますかね
僕の目論見としては、7音音階ベースで曲作るのをやめない?っていうのを
固める10音音階のセオリーがアツいですね
この記事に含まれる概念、隅々に目を通そうとすると
なかなかマスマティックな世界が広がっていますので
さらなる深みが見たい方はこちらからどうぞ。
◆〆
ということで、22平均律のスケール論を軽く話してみました
次回記事では、ダイアトニックコードのように和音の話を展開するとしまして、
今まで僕が扱ってきた平均律(24,31,53)と明らかに違うのは
このスケール論の存在、
数が多いとどうしても和音メインの話になってしまいますが
24よりも少ない22だと、スケールでなんやかんやするという話が盛り上がってきます。
ということで、和音編に進んでいくとしましょう!
