
【量子力学】 球面調和関数
球面調和関数は以下のように与えられている。
$$
\begin{align*}
Y_{l, m}(\theta, \phi) = \sqrt{\frac{(2l+1)}{4\pi}\frac{(l - |m|)!}{(l + |m|)!}}\mathcal{P}^m_l(\cos(\theta))e^{im\phi} ~~~\mathrm{(1)}
\end{align*}
$$
ただし、$${l=0, 1, 2, …}$$は方位量子数(azimuth quantum number)、$${m = -l, …, l}$$は磁気量子数(magnetic quantum number)、$${\mathcal{P}_l^m}$$はルジャンドル多項式(Legendre polynomials)である。
この記事では、球面調和関数(spherical harmonics function)を求める。球面調和関数は、極座標で表現された波動関数のうち角度部分の関数である。
まず、水素原子のシュレディンガー方程式から変数分離して、その後変数ごとに解く。次に、これらの変形された式の中で、上に述べた量子数がどのように関係しているのかを説明する。最後に、得られた解から電子軌道の形を示す。。
概要だけを知りたい人は、導出部分を読み飛ばしてもらって構わない。
1. 水素原子のシュレディンガー方程式
一般的な三次元のシュレディンガー方程式は以下の通り。
$$
\begin{align*}
-\frac{\hbar}{2m}\nabla^2 \Psi + V\Psi = E\Psi~~~\mathrm{(2)}
\end{align*}
$$
電子は、原子核の電荷から力を受け、距離$${r}$$に反比例するポテンシャルを得る。このようなポテンシャルをクーロンポテンシャル(Coulomb potential)と言う。クーロンポテンシャルは、他の短距離のポテンシャルとは異なり、原理的には無限遠にまで影響を及ぼす。
クーロンポテンシャルは次のように表せる
$$
\begin{align*}
V(r) = -\frac{Ze^2}{4\pi\varepsilon_0}\frac{1}{r}~~~\mathrm{(3)}
\end{align*}
$$
ここで、$${e}$$は電気素量(elementary charge, $${\approx 1.602 \times 10^{-19}\mathrm{C}}$$)、$${\varepsilon_0}$$は誘電率(permittivity, $${\approx 8.85 \times 10^{-12}\mathrm{F/m}}$$)、$${Z}$$は原子核の電荷数である。
ヘリウムイオン$${\mathrm{He^+}}$$やリチウムイオン$${\mathrm{Li^{2+}}}$$などは、原子核の周りを回る電子が一つであり、水素原子と同じモデルで考えることができる。これらを水素類似原子(hydrogen-like atom)と呼ばれる。原子核にある陽子の数、そして結果的に原子核の電荷が違うので、$${Z}$$をかけなければならない。ヘリウムイオン、リチウムイオンはそれぞれ$${Z=2,~Z=3}$$である。
今回は水素原子について考察しているので$${Z=1}$$であり、以降書かない。
2. 変数分離
まず、シュレディンガー方程式を直交座標から極座標に変換しなければならない。クーロンポテンシャル$${V(r)}$$は方向によらない球対称な関数であり、結果的に波動関数$${\psi(\mathbf{r})}$$も球対称性が強い関数になるからだ。

ラプラシアンの極座標表示は以下のようになる。
$$
\begin{align*}
\nabla^2 = \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2 \frac{\partial}{\partial r}\right) + \frac{1}{r^2\sin(\theta)}\frac{\partial}{\partial \theta}\left(\sin(\theta) \frac{\partial}{\partial \theta}\right) + \frac{1}{r^2 \sin^2(\theta)}\frac{\partial^2}{\partial \phi^2} ~~~\mathrm{(4)}
\end{align*}
$$
ちなみに、$${r}$$を動径(radius)、$${\theta}$$を方位角(azimuth)、$${\phi}$$を天頂角(polar angle)という。これの導出については本記事では解説しないが、下に参考文献を載せる。
波動関数から角度成分についての関数のみを抜き出すために、変数分離(separation of variables)を行う。すなわち、以下のように$${R,Y}$$を置く。
$$
\begin{align*}
\psi(r, \theta, \phi) = R(r)Y(\theta, \phi)
\end{align*}
$$
すると、以下のように$${R(r)}$$と$${Y(\theta, \phi)}$$で別々の式が得られる。
$$
\begin{align*}
&\frac{1}{r^2}\frac{dR}{d r}\left(r^2 \frac{dR}{d r}\right) - \frac{2mr^2}{\hbar^2}[V(r) - E]R = l(l+1)R\\
&\frac{1}{Y}\left\{ \frac{1}{r^2\sin(\theta)}\frac{\partial}{\partial \theta}\left(\sin(\theta) \frac{\partial}{\partial \theta}\right) + \frac{1}{r^2 \sin^2(\theta)}\frac{\partial^2}{\partial \phi^2}\right\} = -l(l+1) ~~~\mathrm{(5)}
\end{align*}
$$
(導出)
変数分離したものをEq.(4)に代入すると、
$$
\begin{align*}
-\frac{\hbar^2}{2m}\left[ \frac{Y}{r^2}\frac{\partial}{\partial r}\left( r^2 \frac{\partial R}{\partial r} \right)+ \frac{R}{r^2 \sin(\theta)}\frac{\partial}{\partial \theta}\left( \sin(\theta) \frac{\partial Y}{\partial \theta} \right) + \frac{R}{r^2\sin^2(\theta)}\frac{\partial^2 Y}{\partial \phi^2}\right] + V~RY = E~RY
\end{align*}
$$
両辺に$${-\frac{2mr^2}{\hbar^2}\frac{1}{RY}}$$をかけて整理すると、
$$
\begin{align*}
\left\{ \frac{1}{R}\frac{\partial}{\partial r}\left( r^2 \frac{\partial R}{\partial r} \right) - \frac{2mr^2}{\hbar^2} [V(r) - E] \right\} + \frac{1}{Y}\left\{ \frac{1}{ \sin(\theta)}\frac{\partial}{\partial \theta}\left( \sin(\theta) \frac{\partial Y}{\partial \theta} \right) + \frac{1}{\sin^2(\theta)}\frac{\partial^2 Y}{\partial \phi^2}\right\} = 0
\end{align*}
$$
最初の括弧内は変数が$${r}$$だけの部分で、次の括弧内は変数が$${\theta,\phi}$$だけの部分である。これらの変数は独立に動いてこの等式を成立させているから、天下りだが両者がそれぞれ$${l(l+1)}$$と$${-l(l+1)}$$($${l}$$は定数)と置いても差し支えない。よってEq.(5)が得られた。
導出おわり
さらにEq.(5)に変数分離を施す。$${Y(\theta, \phi) = \Theta(\theta)\Phi(\phi)}$$とおくと、以下が得られる。
$$
\begin{align*}
&\frac{d^2\Phi}{d\phi} + m^2\Phi = 0 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{(6)}\\
&\frac{1}{\sin(\theta)}\frac{d}{d\theta}\left(\sin(\theta)\frac{d\Theta}{d\theta}\right) + \left(l(l+1) - \frac{m^2}{\sin^2(\theta)}\right)\Theta = 0 ~\mathrm{(7)}
\end{align*}
$$
(導出)
Eq.(5)に代入すると、
$$
\begin{align*}
\frac{\Phi}{\sin(\theta)}\frac{d}{d \theta}\left(\sin(\theta) \frac{d\Theta}{d \theta}\right) + \frac{\Theta}{\sin^2(\theta)}\frac{d^2\Phi}{d \phi^2} = -l(l+1)
\end{align*}
$$
これに$${\frac{\sin^2(\theta)}{\Theta\Phi}}$$をかけると
$$
\begin{align*}
\frac{1}{\Theta}\sin(\theta)\frac{d}{d \theta}\left(\sin(\theta) \frac{d\Theta}{d \theta}\right) + \frac{1}{\Phi}\frac{d^2\Phi}{d \phi^2} = -\sin^2(\theta)l(l+1)
\end{align*}
$$
ここで、左辺第一項は$${\theta}$$のみの関数、左辺第二項は$${\phi}$$のみの関数、そして右辺は$${\theta}$$のみの関数である。$${\theta, \phi}$$はそれぞれ独立して変化する変数なので、分けて考えることができる。すなわち、定数$${m}$$を置いて、
$$
\begin{align*}
&\frac{1}{\Phi}\frac{d^2\Phi}{d\phi} = -m^2 \\
\Rightarrow &\frac{d^2\Phi}{d\phi} + m^2\frac{1}{\Phi} = 0
\end{align*}
$$
これで、Eq.(6)を得た。また、
$$
\begin{align*}
&\frac{1}{\Theta}\sin(\theta)\frac{d}{d \theta}\left(\sin(\theta) \frac{d\Theta}{d \theta}\right) + \sin^2(\theta)l(l+1) = m^2 \\
\Rightarrow &\frac{1}{\sin(\theta)}\frac{d}{d \theta}\left(\sin(\theta) \frac{d\Theta}{d \theta}\right) + l(l+1)\Theta = \frac{m^2}{\sin^2(\theta)}\Theta \\
\Rightarrow &\frac{1}{\sin(\theta)}\frac{d}{d\theta}\left(\sin(\theta)\frac{d\Theta}{d\theta}\right) + \left(l(l+1) - \frac{m^2}{\sin^2(\theta)}\right)\Theta = 0
\end{align*}
$$
これで、Eq.(7)が得られた。
導出おわり
3. 方位量子数・磁気量子数
ここで、電子軌道の角運動量について考える。シュレディンガー方程式で表現されている運動エネルギーとポテンシャルの中には、角運動量由来のエネルギーも含まれている。この角運動量由来のエネルギーも、離散的な値を持つことが知られている。
加えて、角運動量はベクトルであるため、当然向きもある。この向きの取り方も離散的である。
これらのことについてもう少し詳しく説明する。Eq.(5)の動径方向についての関数を展開・変形すると、次のような式が得られる。
$$
\begin{align*}
-\frac{\hbar^2}{2m}\frac{d^2u}{dr^2} + \left[V(r) + \frac{\hbar^2}{2m}\frac{l(l+1)}{r^2}\right]u = Eu ~~~\mathrm{(6)}
\end{align*}
$$
ただし、$${u(r) = rR(r)}$$。ここで、[]括弧の部分は有効ポテンシャル(effective potential)と言う。式の導出と有効ポテンシャルについては、次の記事でまとめたので参照してほしい。
この式は、古典力学におけるハミルトニアンのこれは、遠心力ポテンシャル(centrifugal potential)に相当する。角運動量$${L}$$による遠心力ポテンシャルは次のように定義できる。
$$
\begin{align*}
U = \frac{L^2}{2mr^2}
\end{align*}
$$
よって$${L = \sqrt{l(l+1)}\hbar}$$と置くことができる。この時、$${l}$$を方位量子数(azimuthal quantum number)と言う。これが、電子軌道の持つ角運動量を決定する。
一方で、Eq.(5)にさらに変数分離を施した二つの方程式のうち、方位量子数はEq.(6)、つまり$${\Theta(\theta)}$$の関数を、ひいては確率密度関数の方位方向の形を決定する。これが、$${l}$$が方位量子数という名前を持つゆえんである。
動径方向の関数をラゲール陪多項式を用いて解くことによって、$${l}$$が非負の整数でかつ主量子数$${n}$$より小さくなければならないということがわかった。従って、たとえば$${n = 4}$$の場合、電子軌道は次のような角運動量を許される。
$$
\begin{align*}
&l = 0 \Rightarrow L = 0\\
&l = 1 \Rightarrow L = \sqrt{2}\hbar \\
&l = 2 \Rightarrow L = \sqrt{6}\hbar \\
&l = 3 \Rightarrow L = 2\sqrt{3}\hbar
\end{align*}
$$
注意してほしいのは、電子の持つ角運動量が0になり得るということだ。電子は、古典力学のようにある軌道に沿って原子核の周りをぐるぐると円運動をしている訳ではない。その代わり、電子の存在は確率密度関数で表される。
角運動量$${l}$$がゼロの時、電子の確率密度関数は原子核を中心としてボール状に球対称に広がっている。その結果、あらゆる方向に電子が等確率で存在・運動しているので、結果的に角運動量は相殺されるのである。
その点で、ボーアの原子モデルは正しくない。

次に、角運動量の向きについて考える。角運動量のz方向の成分を$${L_z}$$と表すと、
$$
L_z = m\hbar~~~(m \in \mathbb{Z})
$$
と表すことができる。当然、z方向の成分が元のベクトルの長さより長くなることはできないので、$${|m\hbar| \leq \sqrt{l(l+1)}\hbar}$$を満たさなければならない。$${m}$$が整数であることを考えると、
$$
m = -l, -l+1, …, l - 1, l
$$
の$${2l + 1}$$通りの値が許されることが分かる。このことは、次のような図を考えると理解しやすい。

注意してほしいのは、角運動量の向きというものが「何に対して」の向きかということだ。私たちは、任意に定めた向きに対してz方向と便宜的に名前をつけているに過ぎない。通常の場合、角運動量がどの方向に向いているかは重要ではなく、軌道にある電子のエネルギー量にも影響を及ぼさない。
しかし、外部から一定方向に磁場が加えられたりして、空間に恣意的な方向づけがされた時に、縮退が解けて、電子の角運動量の方向が意味を持つようになる。磁場の向きに対する角運動量の向きの違いによって、電子の持つエネルギー量が変わる。これがゼーマン効果(Zeeman effect)である。
ゆえに、角運動ようの方向を決定する量子数を磁気量子数(magnetic quantum number)と呼ぶ。
4. Θ関数の解
結論として、
$$
\Theta(\theta) = \sqrt{\frac{2l+1}{2}\frac{(l - |m|)!}{(l + |m|)!}}\mathcal{P}_l^m(\cos(\theta))~~~\mathrm{(8)}
$$
である。以下にその導出を示す。
まず、$${\xi = \cos(\theta)}$$と置換する。このとき、$${\theta}$$は球のしたから上へと動く角度の変数なので、その定義域は$${[0, \pi]}$$である。だから、$${\xi}$$の定義域は$${[1, -1]}$$であることに注意する。すると、Eq.(7)は次のように書き換えられる。
$$
\begin{align*}
\xi^2\frac{d^2\Theta}{d\xi^2} + 2\xi\frac{d\Theta}{d\xi} + \left[l(l+1) + \frac{m^2}{1-\xi^2}\right]\Theta = 0 ~~~\mathrm{(9)}
\end{align*}
$$
ここで、ルジャンドル陪多項式の微分方程式は以下のような形である。
$$
\begin{align*}
x^2\frac{d^2P_{~l}^{~~m}}{dx^2} + 2x\frac{dP_{~l}^{~~m}}{dx} + \left[l(l+1) + \frac{m^2}{1-x^2}\right]P_{~l}^{~~m} = 0
\end{align*}
$$
よって、$${\xi = \cos(\theta)}$$でもあるので、
$$
\Theta(\theta) = C_l^m P_{~l}^{~~m}(\cos(\theta))~~~\mathrm{(10)}
$$
ということが分かった。
(導出)
$${\xi = \cos(\theta)}$$と置換すると、Eq.(7)は次のように書き換えられる。
$$
\begin{align*}
&\frac{d}{d\theta} = \frac{d\xi}{d\theta}\frac{d}{d\xi} = -\sin(\theta)\frac{d}{d\theta}\\
\therefore~&\sin(\theta)\frac{d}{d\theta}\left[\sin(\theta)\frac{d\Theta}{d\theta}\right] = \frac{d}{d\xi} \left[\cos^2(\theta)\frac{d\Theta}{d\xi}\right]\\
&= \frac{d}{d\xi}\left[(1 - \xi^2)\frac{d\Theta}{d\xi}\right]\\
&= (1 - \xi^2)\frac{d^2\Theta}{d\xi^2} + \frac{d}{d\xi}\left[(1 - \xi^2)\right]\frac{d\Theta}{d\xi}\\
&= (1 - \xi^2)\frac{d^2\Theta}{d\xi^2} + 2\xi \frac{d\Theta}{d\xi}
\end{align*}
$$
これを代入して、Eq.(9)が得られる。
導出おわり
ただし、$${\xi = 1}$$と$${\xi = -1}$$で関数が発散しないためには、$${l = 0, 1, 2, …}$$かつ$${|m| \leq l}$$でなければならない。
また、$${\Theta}$$は波動関数の部分であるため、規格化(normalization)されなければならない。このとき、ルジャンドル陪多項式は以下のような直交性を利用できる。
$$
\begin{align*}
\int_{-1}^1 P_{~l}^{~~m}(\xi) ~P_{~l'}^{~~m}(\xi)~d\xi = \frac{2}{2l+1}\frac{(l + |m|)!}{(l - |m|)!}
\end{align*}
$$
これにEq.(9)を代入することで、
$$
C_l^m = \sqrt{\frac{2l+1}{2}\frac{(l - |m|)!}{(l + |m|)!}} ~~~\mathrm{(11)}
$$
ということが分かる。これらのことをまとめて、Eq.(8)が導出された。
5. φ関数の解
結論として、
$$
\Phi(\phi) = \frac{1}{\sqrt{2\pi}}e^{im\phi} ~~~\mathrm{(12)}
$$
である。導出を下に示す。まず、Eq.(6)より、
$$
\begin{align*}
\Phi(\phi) = Ae^{+im\phi} + Be^{-im\phi}
\end{align*}
$$
特に、$${m = 0}$$のとき、
$$
\Phi(\phi) = A + B\phi
$$
である。しかし、$${\phi}$$は球をぐるっと一周する方向の角度の変数なので、$${2\pi}$$ごとに同じ値出なければならない。この周期的境界条件(periodic boundary condition, PBC)を鑑みれば、まず$${m = 0}$$のとき、
$$
\begin{align*}
&\Phi(2\pi + \phi) = \Phi(\phi) \Rightarrow A + B(2\pi + \phi) = A + B\phi \\
\therefore~&B = 0
\end{align*}
$$
また、$${m \neq 0}$$のとき、
$$
\begin{align*}
&\Phi(2\pi + \phi) = \Phi(\phi) \Rightarrow Ae^{+im(2\pi + \phi)} = Ae^{+im \phi}\cdot e^{2\pi i m} = Ae^{+im \phi} \\
\Rightarrow &e^{2\pi i m} = 1 \\
\Rightarrow &m = 0, \pm1, \pm2, … ~~~\mathrm{(13)}
\end{align*}
$$
であることが分かる。
さらに、定数$${A}$$について考えよう。繰り返し言うと、$${\phi}$$は球をぐるっと一周する方向の角度の変数なので、その定義域は$${[-\pi, \pi]}$$である。よって、定数$${A}$$は
$$
\begin{align*}
&\int_{-\pi}^{\pi} Ae^{im \phi}\cdot Ae^{-im \phi} d\phi = 2\pi A^2 = 1 \\
\therefore~&A = \frac{1}{\sqrt{2\pi}} ~~~\mathrm{(14)}
\end{align*}
$$
これらをまとめて、Eq.(12)が導出できた。
6. 電子軌道と角運動量
$${P_{~l}^{~m}(x)}$$の具体例をいくつか下に示す。

これみ基づいて実際に$${Y_{l, m}(\theta, \phi)}$$を計算してみて、どのような形の関数になるか考察を加えてみる。下のグラフでは、球面の座標を方位方向で切り開いてメルカトル図法のように表現したものである。よって縦軸は「緯度」を示し、横軸は関数の値、つまり確率の大きさを表している。(Fig 4. を見よ)

◆$${l = 0}$$(s軌道)の場合
$$
Y_{0, 0} = \frac{1}{\sqrt{2}\pi}\frac{\sqrt{2}}{2}
$$
よって関数は$${\theta}$$にも$${\phi}$$にも依らず、従って球対称である。

◆$${l = 1}$$(p軌道)の場合
まずm = 0のとき、
$$
Y_{1, 0} = \frac{1}{\sqrt{2}\pi}\frac{\sqrt{6}}{2}\cos (\theta)
$$
よって確率密度関数は$${\cos^2(\theta)}$$に関係し、$${\phi}$$、つまり「経度」方向に依らない。これを$${p_z}$$軌道という。

次に、m=1のとき、
$$
Y_{1, \pm1} = \mp\frac{1}{\sqrt{2}\pi}\frac{\sqrt{3}}{2}\sin (\theta) e^{\pm i\phi}
$$
よって、$${|Y_{1, \pm1}|^2 = \frac{3}{8\pi}\sin^2(\theta)}$$だから、関数は$${\phi}$$に依らず、また$${z}$$軸上($${\theta = 0, \pi}$$)で0になる。よって、確率分布はドーナツ上になる。

さらに、$${Y(1, 1)}$$と$${Y(1, -1)}$$の線形結合もまたハミルトニアン関数である。この実部と虚部が$${p_x}$$軌道と$${p_y}$$軌道である。
$$
\begin{align*}
&p_x: \frac{1}{2} (Y_{1, 1} - Y_{1, -1}) = \frac{1}{\sqrt{2}\pi}\frac{\sqrt{3}}{2} \sin(\theta)\cos(\phi) \Rightarrow |Y_{px}|^2 \propto \sin^2(\theta)\cos^2(\phi) \\
&p_y: \frac{1}{2i} (Y_{1, 1} + Y_{1, -1}) = \frac{1}{\sqrt{2}\pi}\frac{\sqrt{3}}{2} \sin(\theta)\sin(\phi) \Rightarrow |Y_{py}|^2 \propto \sin^2(\theta)\sin^2(\phi)
\end{align*}
$$
よって$${p_x}$$軌道と$${p_y}$$軌道は以下のようになる。

◆$${l = 2}$$(d軌道)の場合
まず、m = 0 のとき、
$$
Y_{2, 0} = \frac{1}{\sqrt{2}\pi}\frac{\sqrt{10}}{4} (3\cos^2 (\theta) - 1)
$$
よって、確率分布は「経度」に依らず、$${\theta}$$に飲み依存する。形は、以下のように、上下に突き出たボウリングピンを帯で結んだような奇特な形になる。これが$${d_{z^2}}$$軌道である。

次に、m = 1 のとき、
$$
Y_{2, \pm1} = \mp\frac{1}{\sqrt{2}\pi}\frac{\sqrt{15}}{2} \sin (\theta) \cos(\theta)e^{\pm i\phi}
$$

よって、これらの線型結合は以下のようになる
$$
\begin{align*}
&d_{zx}: \frac{1}{2}(Y_{2, 1} - Y_{2, -1}) = \frac{\sqrt{30}}{4\pi}\cdot 2 \sin (\theta) \cos(\theta)\cos(\phi) \Rightarrow |Y_{zx}|^2 \propto \sin^2(2\theta)\cos^2(\phi)\\
&d_{yz}: \frac{1}{2i}(Y_{2, 1} + Y_{2, -1}) = \frac{\sqrt{30}}{4\pi}\cdot 2 \sin (\theta) \cos(\theta)\sin(\phi) \Rightarrow |Y_{yz}|^2 \propto \sin^2(2\theta)\sin^2(\phi)
\end{align*}
$$
よって確率分布は次のようになる。$${z}$$軸周りと$${z = 0}$$における$${xy}$$平面($${\theta = 0, \pi/2, \pi}$$)は密度が0である。また、$${d_{zx}}$$の場合$${y}$$軸周り($${\phi = \frac{\pi}{2}, \frac{3}{2}\pi}$$)のときの密度は0であり、$${d_{yz}}$$の場合$${x}$$軸周り($${\phi = 0, \pi$$)のときの密度は0である。

最後に、m = 2のとき、
$$
Y_{2, \pm2} = \frac{1}{\sqrt{2}\pi}\frac{\sqrt{15}}{4} \sin^2 (\theta) e^{\pm 2i\phi}
$$
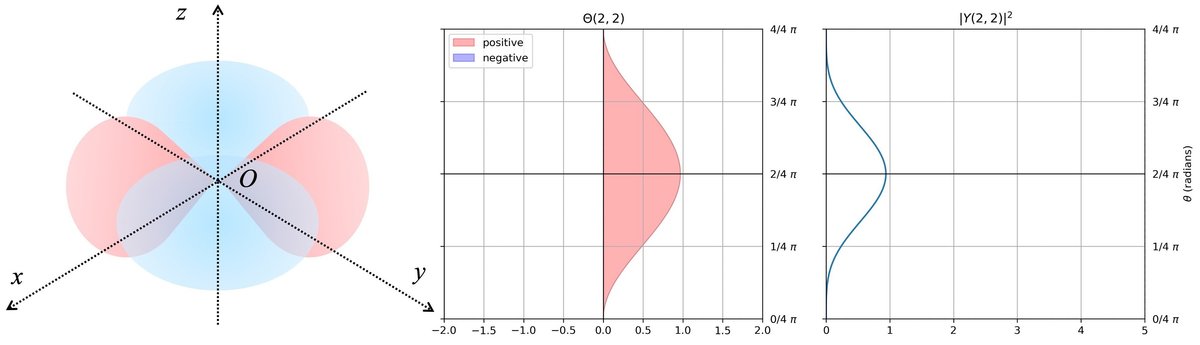
よって、これらの線型結合は次のようになる。
$$
\begin{align*}
&d_{xy}: \frac{1}{\sqrt{2}\pi}\frac{\sqrt{15}}{4}\sin^2(\theta) \cos (\phi) \Rightarrow |Y_{xy}|^2 \propto \sin^4(\theta) \cos^2(2\phi) \\
&d_{x^2, -y^2}: \frac{1}{\sqrt{2}\pi}\frac{\sqrt{15}}{4}\sin^2(\theta) \sin (\phi) \Rightarrow |Y_{xy}|^2 \propto \sin^4(\theta) \sin^2(2\phi)
\end{align*}
$$
よって確率分布は次のようになる。$${z}$$軸周りと$${z = 0}$$における$${xy}$$平面($${\theta = 0, \pi/2, \pi}$$)は密度が0である。
$${d_{xy}}$$軌道を考える。$${Y}$$関数は$${\cos^2(2\phi)}$$に比例するから、$${\phi = \frac{\pi}{4}, \frac{3\pi}{4}, \frac{5\pi}{4}, \frac{7\pi}{4}, }$$で密度が0になる。
$${d_{x^2, -y^2}}$$軌道を考える。$${Y}$$関数は$${\sin^2(2\phi)}$$に比例するから、$${\phi = 0, \frac{\pi}{2}, \pi, \frac{3\pi}{2}}$$、つまりx軸沿いとy軸沿いで密度が0になる。

参考文献
D. J. Griffiths and D. F. Schroeter, "Introduction to Quantum Mechanics", 3rd ed. Cambridge: Cambridge University Press, 2018.
R. Shankar, “Principles of Quantum Mechanics”, 2nd Edition, Plenum Press, New York, 1994.
Schiff, L.I. "Quantum Mechanics", 3rd Edition, McGraw-Hill, New York, 1968
M. Abramowitz I.A. and Stegun, (Eds.) "Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables". Dover Publications Inc., New York, 1965
Whittaker, E.T. and Watson, G.N. "A Course of Modern Analysis". Cambridge U.P., Cambridge, 1935
Howard Haber, "Mathematical Methods in Physics III lecture note", UC Santa Cruz, 2012
原島鮮 著. 初等量子力学. 改訂版, 裳華房, 1987
国広悌二 著. 量子力学, 基幹講座 物理学, 東京都書, 2018
田中宏志. 物理数学I令和2年度版テキスト, 2020
冒頭の画像はhttps://www.toho-u.ac.jp/sci/chem/column/gold_color/032125.htmlから拝借した。
