【公式証明道場1】点と直線の距離の公式【数Ⅱ】
みなさん、こんにちは。「+αで学びたい高校数学のnote塾」支配人のゆーです。
主に週に1回は「公式証明道場」として「知ってるけど考えたことなかった...」というような公式についてしっかり向き合ってみよう!というコーナーです。その初回として「点と直線の距離」をpick up してみました。ぜひ一度、考えてみてくださいね。
まずは、公式の紹介をしましょう!
数学Ⅱの「図形と方程式」で登場する公式ですね。
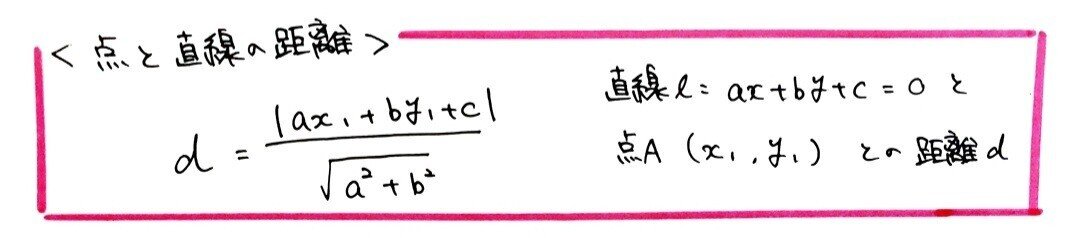
手書きで行うと字の傾き具合が非常にわかりますね。(本当にごめんなさい。)
色んな証明があると思いますが、今回はゴリゴリの計算で超古典的に示していきたいと思います。いくつかのポイントをまとめて証明していきましょう!
Point:① 平行移動して計算を少しでも楽に!!
上の図でいうところの点Aと点Hの距離を求めればいいわけです。ただ、このまま立ち向かってもできるかもしれませんが少し面倒だと思います。そこで、点Aを原点に持ってくるように平行移動しましょう!
(だって、距離っていうのはどこで測っても同じ長さだよね。)
ところで、グラフの平行移動の式をみなさんはご存じですか?確か、1年生の段階でちらっと出てくるはずですが、あんまり意識することはなさそう...しっかり確認しておいてくださいね!

さて、これで準備はばっちり!
しっかり計算ミスせずに、交点を求めてその点との原点との距離を求めていこう!
まずは、直線に対して垂直な直線の方程式を求めていく。

※原点を通る直線の式 ⇒ 比例式 y=ax というのは中学校の範囲ですね。(下2行目)
※2直線が垂直ということは (傾き)×(傾き)=-1となるのが条件です。(下1行目)
では、ここから2直線の交点を求めていきましょう!


なかなか、いかついですけど頑張っていきましょう。最後に、原点からこの点の距離を求めていきましょう!

※絶対値になるのは、分子の中身がプラスになるかマイナスになるかがわからないからです。
みなさん、どうでしたか?一度、公式に向き合うのも大事ですね!
間違っていたら、コメントで教えていただけると幸いです。
