【定義微分】sin xの導関数【数Ⅲ】

2021年1月8日 19:24

みなさん、こんにちは。「＋αで学びたい高校数学のnote塾」支配人のゆーです。

今回は「様々な関数を導関数の定義に従って微分するシリーズ」を行っていきたいと思います。

第１回目はsinの微分を行っていきたいと思います。学校の授業では証明まではしなかったと思うので（ずいぶん昔の記憶ですが...。）ある意味、公式のように覚えているものです。そんな公式と向き合うのが本noteの役割の１つでもありますのでどうやって導かれるのか確認していきましょう！

今回の証明のなかで sin x / x の極限値を使いますので、なぜそうなっているのか気になるという人はまずこちらをご覧ください。

では、今回微分する関数を見ていきましょう！

なんと、不思議ですよね！sinを微分するとcosが出てくるという！つまり、sinのグラフの傾きを求めようとしたときに、その傾きがcosのように変化していくということですよね！素晴らしい！（置いてけぼりなら、すみません。）

では、さっそく取り掛かりましょう！

そもそも、導関数というのは（傾きを求めようとする式）からスタートします。私はくせで1行目は（xの増加量）も（yの増加量）も

「（変化後）ー（変化前）」

というように書きますので、ある意味1行無駄かもしれませんがお付き合いください。

数Ⅲの記述問題にもなれば、かなり1行の式の長さがあまりにも長いので抜き出して1部分だけ考えるときもあります。

今回は、(cos h -１) / hの部分について考えています。

ここの1行目は分子の2項目の符号違いのやつを分母にも分子にも掛け算しています。（虚数の範囲でいうところの共役関係？）

この戦法を僕個人的な呼び方で「逆有理化」なんて呼んでいます。（もはや有理化でもなんでもないですが、分子に関するものを分母分子両方に掛け算しているので...。）正式な解法の名前があれば教えてください。

これにより、式の前半部分（＋より前の項）の値が０で」あることがわかりました。あとは、後半部分（＋より後ろの項）だけですね！

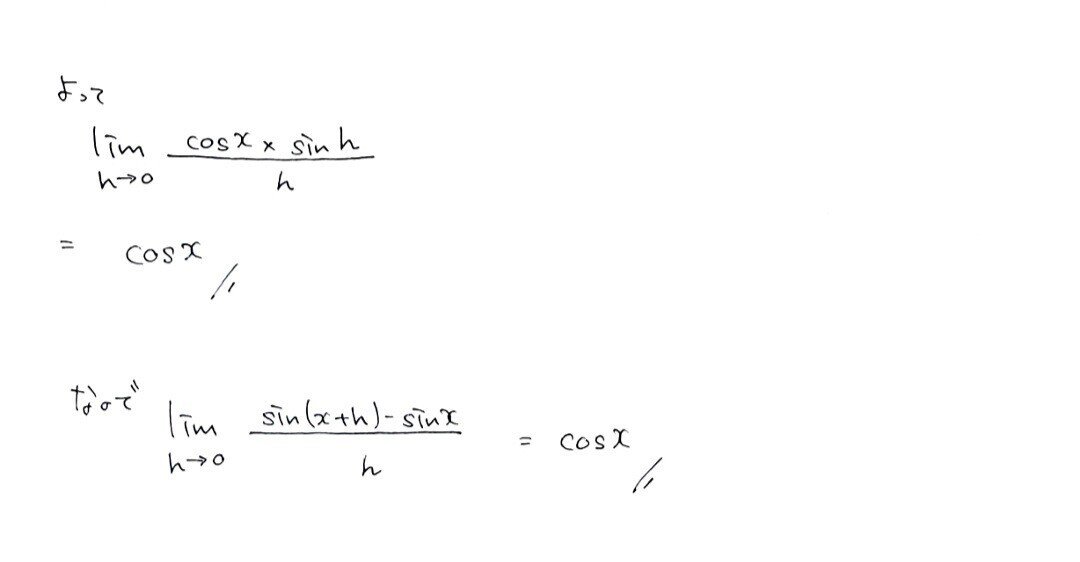
お！これが前にやった部分ですね！きれいに決まりました！以上で証明終了です！！お疲れさまでした！！

今後も、こういった「導関数の定義に従った微分」を行っていきますのでお楽しみに！！