信号検出理論の説明（type 1）

（本記事は過去に別アカウントで作成した記事に加筆・修正をしたものです）

信号検出理論とは

信号検出理論（SDT: Signal Detection Theory）について，ここでは特に心理学の領域から説明する。信号検出理論とは，例えば今見ている画像は以前見たことがあるものか否かを判断するような，特定の刺激（signal）の有無（present / absent）を区別するプロセスをモデル化したものである。

上の例で「signal があったかどうか」を回答させることを考えると，実際の正誤に関わらず present と回答しやすい人もいれば absent と回答しやすい人もいると考えられる。この時，信号検出理論に基づく測定を行うと，回答者が持つ実際の弁別力（signal の有無を判別する能力）とバイアス（present または absent と回答しやすい傾向）とを独立に算出することができる。

信号検出理論の3つの仮定

信号検出理論は，以下の3つの仮定で成り立っている。

1. 外部から刺激が入力された際に，その刺激に対応する心理量が生じる。

2. その刺激が signal である場合は signal ではない（すなわち noise である）場合よりも生じる心理量が大きい。

3. 生じる心理量には誤差があり一定ではないが，この誤差は正規分布に従い，刺激が signal である場合と noise である場合とでその分散は等しい。

これを図で表すと次のようになる（図1）。

図1  正規性と等分散性が仮定された心理量の分布。N分布: 刺激が noise である時の分布（破線）。S+N分布（またはSN分布，S分布）: 刺激が signal である時の分布（実線）。

判断基準と反応タイプ

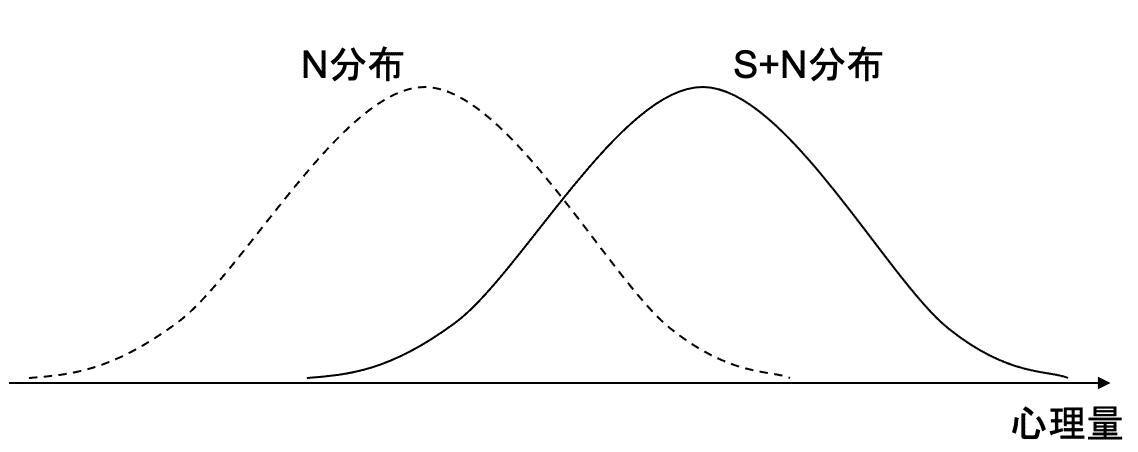
前述の仮定の下，さらにある一定以上の心理量が生じた場合は signal がある（present）と判断し，一定量未満の心理量の場合は signal がない（absent）と判断する基準があるとすると，回答者の反応は4つに分けることができる（図2）。なお，図2について，本来はN分布とS+N分布は図1のような互いに重なり合う配置となるが，図示における明確さを考慮して各分布を別々に配置したことには注意されたい。

図2  回答者の判断基準と反応タイプ。Hit: 刺激が signal である時に present と判断。False Alarm: 刺激が noise である時に present と判断。Miss: 刺激が signal である時に absent と判断。Correct Rejection: 刺激が noise である時に absent と判断。

signal の判別を何度も行うことで，4つの反応がどの程度生じるのか，その確率を算出することができる（表1）。

表1  反応タイプのマトリックス

弁別力とバイアス

信号検出理論において，弁別力はN分布とS+N分布とが心理量の軸上でどの程度離れているか，すなわちN分布・S+N分布間の距離として考えられている。これは感度（sensitivity）と言われ，その指標には"d'（ディー・プライム）"が用いられる。これと同時に，回答者の判断基準がどれだけ偏ったものであるのか，すなわちバイアスを示す指標である"c（または criterion）"も独立に考えることができる（図3）。

図3  d’とcriterion。N分布とS+N分布の交点に位置する点がバイアスの基準値（黒縦破線）。判断基準がこの基準値からどれだけズレているかがバイアスを示す（黒縦破線から青縦破線までの距離）。

d'の計算方法

N分布・S+N分布間の距離は各分布における心理量の平均値の差で考えることができるので，

d' = (S+N分布における心理量の平均値) - (N分布における心理量の平均値) … (1)

となる（厳密にはこれをN分布の標準偏差で除するのだが，慣例的に両分布の標準偏差は1とされているので無視してよい）。

ここで，Hit率とFA率を標準化する（厳密には，正規分布の逆関数を考える）ことで，各分布の心理量の平均値から判断基準までの距離がわかる（図4）。

図4  各分布と確率の標準得点の関係の例。p(H)の領域とp(FA)の領域は重なっていることに注意。

判断基準の位置を基準に見ると，S+N分布における心理量の平均値はz(p(H))だけ離れた位置にあり，N分布における心理量の平均値はz(p(FA))だけ離れた位置にあることがわかる。なお，図4のような場合にはN分布における心理量の平均値が判断基準よりも左側（負の方向）に位置していることからz(p(FA))は負の値となることがわかるが，この点は図5も参考にされたい。

図5  確率密度に関する参考図。

したがって，式(1)は 次のように表すことができる。

d' = z(p(H)) - z(p(FA))

d' が大きいほど感度が高い（＝弁別力が高い）ことを表し，d' = 0 はチャンスレベルである（signal と noise の区別ができていない）ことを表す。

図4を見ると，d' = |z(p(H))| + |z(p(FA))| とできるようにも思われる。しかしながら，例えば判断基準がS+N分布における心理量の平均値の位置よりもさらに右にある場合を考えてみると，単なる絶対値の和では一般化できないことがわかる。

（余談だが，d' の d は"discriminability index"の d だとか（要出典））

criterionの計算方法

バイアスの指標である criterion は回答者の判断基準がN分布とS+N分布との交点となる位置からどれだけ離れた位置にあるかを表す（criterion と判断基準とを混同する間違いがしばしば見られるが，criterion はN分布とS+N分布との交点となる位置と判断基準との距離であることには注意されたい）。

図3, 4から以下のように表すことができる。

• z(p(H)) = d'/2 - (判断基準)

• z(p(FA)) = -(d'/2 + (判断基準))

したがって，criterion は以下のようにして求めることができる。

c = -1/2 × [z(p(H)) + z(p(FA))]

c = 0 は判断基準がN分布とSN分布の交点に位置する，すなわちバイアスがないことを示す。

c > 0 の場合は保守的 (conservative) なバイアス，すなわち signal ではなかった (absent)と判断しやすいバイアスであることを示す。

c < 0 の場合はリベラル (liberal) なバイアス，すなわち signal であった (present) と判断しやすいバイアスであることを示す。

なお，ここまでの計算については図6を参考にするとわかりやすいかもしれない（ただし，図6の判断基準の表現は上の式にしたがったものであることには注意されたい: 厳密には青破線が判断基準を示し，黒破線・青破線間の距離は criterion を示す）。

図6  d' および criterion を算出する式の考え方の参考図

その他

signal が present か absent かを判断する課題はタイプ１の課題（type 1 task）とされ，上記の各パラメータは全て type 1 のものとなる。type 1 での判断に対する確信度，すなわちどれだけの自信を持って present / absent と言えるのかを評価する課題はタイプ２の課題（type 2 task）とされる。

また，今回取り扱ったものは等分散・正規分布を仮定したモデルであることには注意されたい。

参考文献

• Macmillan, N. A., & Creelman, C. D. (2005). Detection theory: A users guide (2nd ed.). Lawrence Erlbaum Associates, Inc., US: New York.

• 草薙邦広・ 後藤亜希 (2015). 「外国語教育研究と信号検出理論」, 外国語教育メディア学会 (LET)関西支部 メソドロジー研究部会2015年度 第8号報告論集，pp.20–36.

• とある基礎系心理学者. (2022). #14-S　わかりやすく！信号検出理論. https://note.com/toaru_gakusya/n/n844ff85d2e8d

• Chandler, J. (2013). Signal Detection Theory October 10, 2013 Some Psychometrics! Response data from a perception experiment is usually organized in the form of a confusion. https://slideplayer.com/slide/7704409/