
レイマーチングの復習
久方ぶりにUnityを更新したのでレイマーチングについて書く。
光を制するものはレンダリングを制するのだ。
光の反射
レイマーチング(ray marching)はレイトレーシング(ray tracing)の一種である。レイトレーシングの前に、普通のシェーディング(shading)について説明する。ゲームのような3Dグラフィックを計算するとき、色(color)をどう計算しているか。
シェーディング
光は物質にあたった時、いろいろな方向に反射する。
このことを前提に陰影を計算する簡単な例がこれ

白色光(例えば太陽光)が物質に当たると、物質の色に対応した光が拡散する。上の図でいうと、太陽光が緑色の物質にあたってこれが反射したものが目に入る(よって、緑色と認識する)。
反射した光はいろいろな方向に飛ぶが、目で見る場合は目の方向に飛んだ光だけに注目すれば良い。計算するときは次の3つを使う
物質表面の向き(法線)
物質表面から見た、太陽光の方向
物質表面から見た、目(カメラ)の方向
目から見て、最も手前にある物質の表面を一度だけ計算すれば良い。
レイトレーシング
こういう場合はどうか

現実では、白い物質が薄い緑っぽく見えそうだが、さっきの計算だと太陽光の直接反射しか計算しないから緑の部分は全く反映されず真っ白になる。
これがゲームの質感がリアルっぽくない理由になる。現実の環境は複雑な光の反射によって成り立っている。逆に、リアルっぽいゲームはこれを何らかの方法で擬似的に解決している。
2回反射することを考えるなら、2回計算すれば良い。

このように光を追跡することで最初の単純な計算よりもずっとリアルな計算結果が得られる。ただし、異なる経路が無数にあるため、本当に厳密な計算を行うのは極めて難しい。

ただ、主要な経路を計算できればそれなりに近似できる。ここで、レイトレーシングの例として光が何回か反射する状況を書いたが、今回のレイマーチングは特に光が何回も反射したりはしない。
レイマーチング
距離関数
レイマーチングはレイトレーシングの具体的な手法の一つである。レイマーチングのキーワードは距離(distance)。世界を距離で記述する。
普通、3Dの物体(object)を表現するときは頂点(vertex)の集合として扱う。一方、レイマーチングにおける物体は距離関数(distance function)である。なにをいっているのか。
こういう状況を考える
カメラが座標$${(0, 0, 0)}$$、方向$${(0, 0, 1)}$$
球形の物体が半径$${1}$$、座標$${(0, 0, 10)}$$

このとき、球形の物体を次のように定義する
$$
d(x, y, z) = \sqrt{ x^2 + y^2 + (z - 10)^2} - 1
$$
この関数は座標$${(x, y, z)}$$が物体の内側にある場合に負、外側にある場合に正、境界上で$${0}$$になる。符号があるので正確には符号付き距離関数(signed distance function)という。
スフィアトレーシング
最初は光源を入れずに物体は白、それ以外は黒という環境を考えて物体を描画してみる。基本的な考え方は「物体との距離だけはわかるとして、距離に応じて少しずつ前に進む」。
カメラが適当な画角をもっているとして

まず
カメラの位置をレイ(光)の位置とする
次を何回か繰り返す
レイの位置と物体の距離を計算する
距離の分だけレイをカメラ方向に進める
こうするといずれ物体に当たる(距離が0になる位置に収束する)

収束しなかったときは物体に当たらなかったということになる

この方法をスフィアトレーシング(sphere tracing)という。この手法では、距離関数が正を返すときに最小の距離を返してくれないと困るということがわかる。
基本的な形状とオペレータ
もう少し複雑な図形、例えば2つの球を描画したいときは
$$
d(x,y,z) = \min(\sqrt{x^2 + y^2 + (z - 10)^2}, \sqrt{x^2 + (y - 5)^2 + z^2}) - 1
$$
とすれば良い。
実用的には、基本的な形状と処理の組み合わせで最終的な距離関数を作る。ここではいくつかの形状とオペレータを紹介する。
半径$${r}$$の球形
$$
d_S(x, y, z) = \sqrt{x^2 + y^2 + z^2} - r
$$
平行移動
$$
d_T(x, y, z) = d(x + t, y, z)
$$
結合、2つの物体の両方を描画する(minimum)
$$
d_U(d_1, d_2) = \min(d_1, d_2)
$$
スムーズな結合、2つの物体を境界を滑らかにしてつなげる(soft minimum)
$$
d_{U'}(d_1, d_2) = - \alpha^{-1} \log (\exp(-\alpha d_1) + \exp(-\alpha d_2))
$$
他にもいろいろあるので調べてみよう。
レイマーチングの距離関数、基本的な形状とオペレーターを教えて
法線と陰影
光源を考慮して陰影を計算しよう。
スフィアトレーシングで表面の位置はわかったとして、法線を計算する。表面上の点から十分小さい距離$${\Delta d}$$だけ適当にずらしたときに、距離がもっと大きくなる点が法線の方向になる。
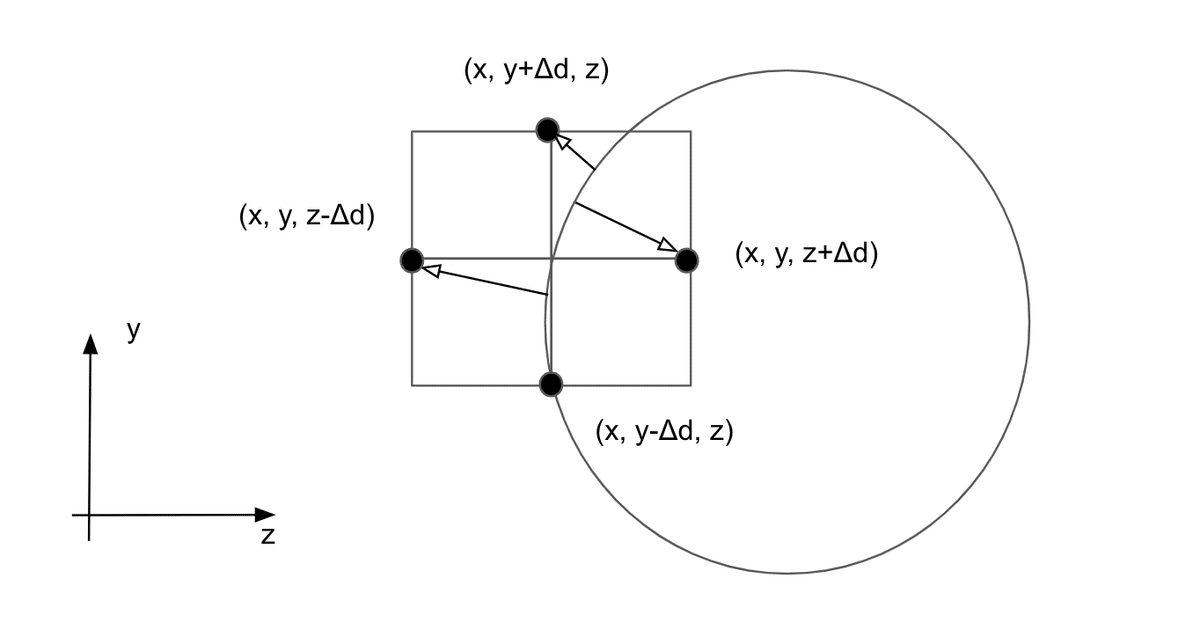
実用上は3方向(6方向)をとって
$$
u_x = d(x + \Delta d, y, z) - d(x - \Delta d, y, z)
$$
$$
u_y = d(x, y + \Delta d, z) - d(x , y - \Delta d, z)
$$
$$
u_z = d(x , y, z + \Delta d) - d(x , y, z - \Delta d)
$$
で良い(長さは正規化する)。
法線が計算できれば、カメラ方向と光源方向はすでにわかっているはずなので陰影を計算できる。

deferred renderingなら材質(albedo、glossiness、emission、normal)だけをパラメータとして、陰影計算を後に回せるので楽。UnityのPBRなら後の計算はUnityがやってくれる。
普通の物体
レイマーチング以外の描画(普通のポリゴンを使ったレンダリング)と組み合わせることを考える。
これは簡単で、深度(depth)を計算すれば良い。物体の表面上の位置はワールド座標として得られるが、これとカメラとの距離が深度である。その上で、手前にあるもの(深度が低いもの)を描画するようにする。

また、深度が適切に計算できれば影(shadow)も適切に計算できる。

テクスチャを使う
UV座標を何らかの形で定義できればテクスチャからサンプルできる。

(自分は)とりあえず良い方法が思いつかなかったので画像中のUVは適当、normal mapを使うと簡単に質感を出せる。
おわりに
7年前に書いておくべき?そのとおり、すまない
レイマーチングは絵的な面白さとともに自分で実装すると学びになる。
当時、実装した部分はこのあたり
工夫すると色々遊べる。
おまけ
影について少し書いておく
影があるかどうかは、物体の表面と光源の間に遮蔽物があるかで決まる

太陽側から計算する方法と物体側から計算する方法があるが、いずれにしても表面の座標は必要である。
また、深度が適切に計算できれば影(shadow)も適切に計算できる
これは言葉が足りていなくて、カメラの位置と方向と深度から表面の座標を計算できるというだけ
手法の一つ、太陽側から計算する。まず、太陽から見て光の当たっている場所を考える

太陽は平行光源だから1枚の深度のマップを作成できる。これは光が当たっている場所から太陽に対する擬似的な距離である。

次に、対象の物体表面から見て太陽への距離を計算する。このとき、さっき計算した距離と一致していればそこは光が当たっている。それよりも遠ければ遮蔽物があり光が当たっていない。
