
ねこひねりの物理学
なぜ我々は三角関数や運動方程式を学ぶのか?
なんの役にも立たないのではないか?
それはねこを知るためにあったのだ
問題
人類は経験的に知っていた
ねこは落下するときに足側から着地する
さらに
落ちる瞬間は全く回転しておらず、背中側から落ちたとして
空中で体を捻る動作だけで、足側から着地できる
これが明らかになるのは、十分に解像度の高い撮影が可能になった後である。時は1894年。
それまでは足で蹴るなど多少回転がついているとか尻尾を振ってその反動を利用しているとか思われていたらしい。撮影された後でもそう思っていた人がいたらしい。
なぜこう思うのかというと
落下の瞬間に回転していない → 角速度がゼロ
途中で回転している → 角速度がある
角運動量が保存されていない。ねこは物理法則を超越するのか。
これに対する解答が示されるのが1969年。

ねこの体のひねりを2つの円柱に見立てて
それぞれの円柱の回転
全体の回転
これらが釣り合っていれば角運動量は保存される。ねこは物理法則に従っていたのだ。
解法
解いてみよう
ここでは密度をもった円柱のようなものを考えずに、単に質点が回転しているという最も単純なモデルを考える。
質量が$${2m}$$の質点が半径$${r}$$を速度$${v}$$で等速円運動しているとする。

このときの角運動量は
$$
L = 2mvr
$$
これを$${x}$$軸の正の方向とする($${x}$$軸を中心に回転しているという意味)。
これを2つに割って逆方向に回転させる。また角度をつける。
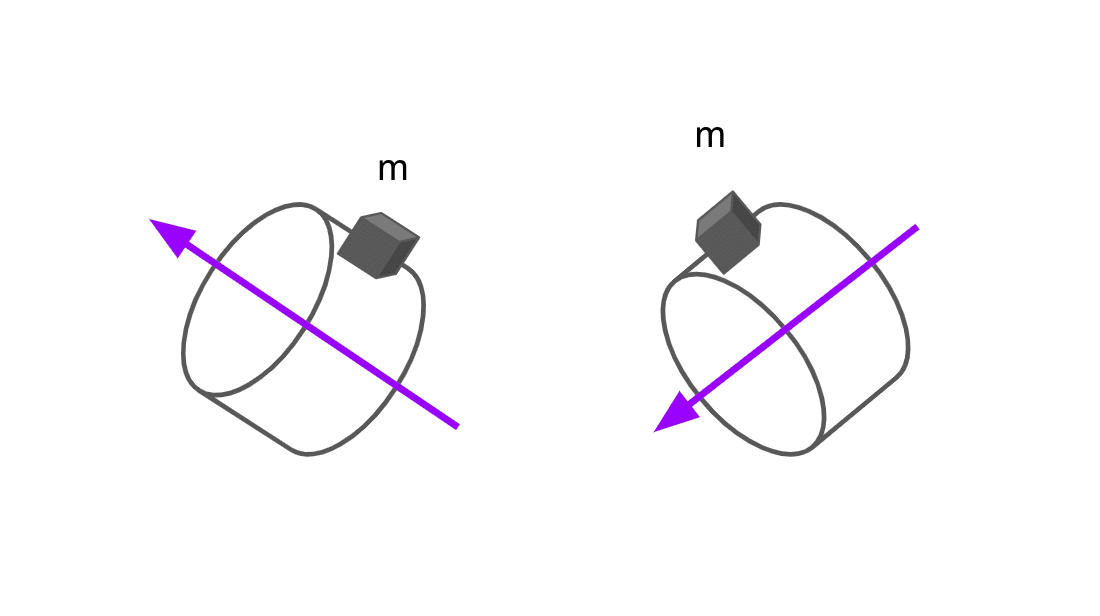
それぞれの質量は$${m}$$、半径は$${r}$$、速度が$${v'}$$、さらに角度が$${\theta}$$とする。左の分の角運動量は$${x}$$軸方向、$${y}$$軸方向のそれぞれで
$$
L_{l,x} = - mv'r \cos \theta
$$
$$
L_{l,y} = mv'r \sin \theta
$$
右の分は
$$
L_{r,x} = - mv'r \cos \theta
$$
$$
L_{r,y} = - mv'r \sin \theta
$$
これらが釣り合うから
$$
L + L_{l,x} + L_{r,x} = 2mvr - mv'r \cos \theta - mv'r \cos \theta = 0
$$
$$
L_{l,y} + L_{r,y} = mv'r \sin \theta - mv'r \sin \theta = 0
$$
よって
$$
v = v' \cos \theta
$$
$${\theta = 0}$$のときに$${v = v'}$$となりひねらず、回転もしない。$${\theta}$$が大きいほどひねられる。

実験
確かめてみよう
コード
結果

足が下にくることがわかる。

発展
角運動量を保存しながら体を回す方法はわかったが、これだけだと足から着地できない。
速度$${v}$$と角度$${\theta}$$は
落下の直後にともに$${0}$$
足が下に向くまで$${0}$$ではない
足が下に向いたら$${0}$$
こういう状態を作らないといけない。足が下に向いても速度が$${0}$$でないと余分に回転してしまう。速度$${v}$$と角度$${\theta}$$は時刻$${t}$$に対する変数だ。

ロボットをぴったりした位置に止めるみたいなイメージをすると良いかもしれない。
おわりに
ねこはともかく問題を抽象化すると範囲が広いため、21世紀に入っても研究されている。
参考、回転を計算するときに役立つもの
おまけ
Microsoftくんのかんがえる falling cat problem

もうちょっとがんばってくれないか
