月刊『大学への数学』:数学を得意科目にする雑誌
こんばんは、家庭教師のせむです。
今年の受験生の指導に、月刊『大学への数学』(以下、月刊大数)を使用しました。
初めての試みとなりましたが、教えたときの手応え・実際の入試結果ともに、相当満足のいくものになりました。
結論として、偏差値55~の大学を志望する子なら誰でも(もちろん、2次試験で数学が課される大学・学部を受験する子の話です)オススメできる雑誌となります。
今回はそのあたりを、今年度の指導実例とともに紹介したいと思います。
★記事を読む前の大前提:大数シリーズの難易度表記について
大数シリーズでは、問題の難易度を大問ごとにA~Dで設定している。
A……基礎
入試レベルの基礎。あくまで入試基準であり、教科書や傍用問題集・定期テストレベルの中では難し目の問題も含まれる。
共テ/センター試験の半数くらいがこれ。
中堅以下の私大入試も大体これ。
共テで75点~80点くらいまで狙えるレベル。
B……標準
入試の標準。
偏差値50以上の大学は文理問わず・国公私問わず、おおむねすべてB問題が主戦場になる。
B問題とそれに相当する部分(C以上の問題の序盤)を完璧に解答できれば、東大理系含めたほぼ全大学全学部の合格ボーダーを上回る。
つまり、入試勉強の目標は「B問題を確実に完答できる力」を身につけることになる。
Bをすべて完答できれば、共テ満点、2次6割~満点(ほぼ全ての大学で)
C……発展
入試の発展問題。
B完答前提で、C問題が主戦場になるのは医学部医学科の中でも難関のところのみ?
基本的に完答は難しい。もちろん完答できれば大きな差にはなるけど……。
D……難問
入試の難問。
D問題が主戦場になるのは京大理学部の特色入試だけかな??
毎年の入試の最難10問くらいがD問題で、「これくっそムズいわ!」と思った問題でも、その多くはC問題。それくらいの難易度。
※自分が勉強してきた問題難易度を大きく上回る問題であったとしても、途中までは易しかったり、答えを出すだけならどうにかなったりする。試験本番の問題難易度&立ち回りと、学習で扱う問題難易度&立ち回りにはある程度の差があることを理解しておく必要がある。
★要約/まとめ
勢いで書いていたら長くなりすぎたので、先にまとめから。
世間の印象に反して、中堅以上を志望する幅広い学力層で使える
意外と数Ⅲの演習量は多くない。文系でも使える
やや雑味のある問題演習によって、数学を得意科目に仕上げられる
B問題がメイン、AとCはサブ、Dはほとんどない
講義等も入試に役立つものが多い
参考書と併用して同レベル・同単元の補強で使うと良い
◎どういった雑誌なのか?
大数シリーズでは『1対1対応の演習』などがだいぶメジャーな問題集ですが、その大本となる月刊大数はそこまでメジャーな参考書ではありません。
まずはどういった雑誌なのかを確認していきます。
◯月刊大数への世間の印象
僕の月刊大数に対する印象(入試対策をする前)は、
理系の最上位層向け
難問が多い
入試対策の範囲を逸脱しかけている
といったものでした。恐らく、月刊大数を手に取ったことがない多くの方も、同様のイメージを抱いていることと思われます。
実際、「入試対策から逸脱しているレベルの難問」ももちろん収録されています。
ですが、そういった問題はごく少数です。
月刊大数で最も多くページ数が割かれているコンテンツは、スタンダード演習(B問題オンリー)、日々の演習(B~C問題)、数Ⅲ演習(B~C問題)などになります。
まあつまり、月刊大数は、決してC~Dの難問ばかりを集めたような問題集ではなく(そもそも、その年の入試のC~D問題の数は限られています)、入試対策のレベル感として最適な難易度の問題を集めた問題集であると言えます。
◯問題の質
出題内容は最新の入試からとなっています。
狭い範囲からの精選ですので、必ずしも良問揃いとは言えません。
で、これこそが、月刊大数の一番「効く」ポイントだと考えています。
というのも、数学の入試問題の多くは、後世の良問集に収録されない、普通問・悪問だからです。
問題集に収録される良問というのは、「学習効果の高い問題」のことです。
例えばチャートの例題は余計な要素が削ぎ落とされた"基本形"ばかりですので、それを完璧にすれば、他の多くの問題に応用できます。すなわち、チャート例題は非常に学習効果が高いと言えます。
あるいは、メジャーな入試問題集に収録されている問題も、ひとつの問題に様々な別解があったり、本質的な議論の土台になっているものばかりです。これらもまた学習効果の高い問題であると言えます。
ですが、実際の入試問題は学習効果を考えて作られていません。入試は受験生をふるいにかけるための問題であり、入試問題は受験生の得点分布を上から下まで満遍ないものにするために作られた問題です。
そのために、少し工夫が施されていたり、複数の頻出事項が組み合わせられた問題が作成されます。あるいは、小問(1)~(3)で徐々に難しくなっていくような問題が作られたりします。そういった要素を付け足すごとに、問題の学習効果は徐々に減ります。
工夫が施されたり複数事項と組み合わせた問題はいわば「変わり種」の問題であって、「これだけやっておけば類似パターン全部いけます!」といった王道の基本形問題ではありません。また、小問構成の問題も、難易度設定がガバすぎて、(1)から大多数が解けなかったり、逆に(3)だけ激ムズだったりといったこともあります。
合格体験記などでよく言われる「過去問◎◎年分解いたら得点力がついた」という話は、実際には、上記のような普通問や悪問に数多く触れることで、そういった問題に対する対応力がついた、という風に言い換えることができます。
実際、たとえば、問題集をやり込んだ理Ⅲ志望の受験生が満を持して過去問を解いてみたら5割も取れなかったヤバい、なんてことはよくある話です。普通問や悪問に対する耐性が身についていないために、こんなことになります。
で、話を月刊大数に戻すのですが、月刊大数は「最新年度の入試問題から」という縛りを設けているため、良問になりきれなかった問題たちが少なからず収録されます。
このほんのりと問題から香る雑味が、良問揃いの参考書と、普通問悪問の巣窟である過去問の架け橋として効いてくるというわけです。
とくに、高得点で安定したい=数学を得意科目にしたい受験生にとっては、普通問や悪問での得点力は必須です。「はいクソ問~。問題が悪い」なんてダサいことを言う前に、クソ問だろうが良問だろうが解ききるだけの力を身に着けるべきなんですよ。
あとは、そもそも過去問をそんなにたくさん用意できない大学も多いです。旧帝大や早慶以外は大体5年分とか7年分くらいが限界で、そんなもんの量だと、入試の傾向を押さえることはできても、入試問題特有の雰囲気を掴むことはできません。
あるいはここ数年で傾向がブレ過ぎて、過去問演習が全然信頼できない大学もあります。
そういった大学では、過去問演習にこだわりすぎるよりは、月刊大数で幅広い演習を積んだ方が、安定した得点力に繋がるはずです。
◯誰が使うべきか?
文理問わず、国公私問わず、偏差値50以上の数学の2次試験で数学を得意科目にしたい全ての受験生が、月刊大数を使う価値があると言えます。
出題の大半はⅠAⅡBC(ベクトル)からであり、また問題難易度もB問題が主軸になっています。
よって、月刊大数を月刊誌として捉えるよりは、「文理問わず多くの受験生が使用できる、分野別の最新入試問題集」と考えたほうが適切なように思われます。
一応、B問題が主軸ということで、基礎が固まっていない人が扱うにはやや苦しいということは言っておきます。
学習到達度で言えばチャートの例題を一通り解いたくらい。
数学の模試(ハイレベル模試ではない記述模試)で言うなら、得点率60%くらい or 偏差値60くらいであれば十分に取り組めるはずです。
問題量も決して少なくありませんが、このあたりについては下の方でいくつか使用案を挙げていますので、それによってある程度は解消可能だと考えています。
また、家庭教師や塾の先生、あるいは大学生の兄/姉など、疑問点を解消してくれたり解くべき問題を選定してくれる人が身近にいれば、学習がスムーズに進みますので、多めの問題量でも無理なく進めることができます。
◎内容
さて、長々と前置きを語ってしまいました。ここからが本題です。
月刊大数の内容について見ていきます。
◯演習
月刊大数の一番のメイン。
5月~11月は単元別演習、12月~2月は総合演習です。
以下に、それぞれの演習のラインナップ・難易度を挙げます。
6月号(ベクトル)はこんな感じです。
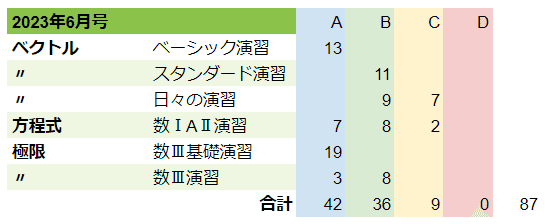
数Ⅲ基礎演習が非常に多いが、小分けされているだけです
文量的にはB問題が最多です
次に総合演習の12月号です。


ベーシック演習が消えて、A問題比率は一気に減る
どの号にしても、B問題が最多です。B問題は中堅以上を志望する全ての受験生が解けるようになるべき問題です。
ほかに講義や読み物の中にも各数問扱われたり(難易度B~C)、学コン・宿題などのエンドコンテンツ(難易度C~Dは)が数問あります。講義については下の方でもう少し詳しく語っています。
1冊あたりの問題数は合計100問ほどになります。
毎月100問といわれれば結構多いと感じるでしょうが、実際のところ、見た目ほど多くはありません。
A~Bが主戦場の子は日々の演習や発展演習を無理に扱う必要はありませんし、B~Cが主戦場の子はベーシック演習を1日でササッと確認できるはずです。その受験生が丁寧に解かなければならない問題は毎月50問も無いはず?1日2問くらい。1ヶ月でやるには丁度よい文量だと言えるはずです。
◯入試問題
月によっては、入試問題を紹介するコーナーがあります。
入試難易度の評価は結構参考になります。問題集と同じ尺度でA~D評価してくれており、学習や対策への解像度は格段によくなると思います。
予備校や赤本の評価はそもそも前年比難易度とかいうあんまり参考にならないものだったり、受験生の不安を煽るための余計な力学が働いて難易度を過小評価してきたりするので、個人的には数学の難易度はこっちを信頼しています。
ほかに、京大理学部の特色入試や数オリ(予選・日本大会・世界大会)の解答・解説も収録されます。
どの参考書にも乗らないようなレベルの問題ですので(数オリはまあ入試ではないので当然ですが)、別の世界を覗いているようで興味深いです。
◯読み物1:講義
テーマ別に深く掘り下げたり、全パターンをしっかり押さえるタイプの記事です。目次の対象bの記事です。
大抵はB~C問題3つほどを扱います。たまに演習問題もつけてくれる講義があります。
この難易度帯で例題→演習の流れを踏めたり(スタンダード演習や数Ⅲ演習のことです)、関連出題パターンを網羅してくれる機会はけっこう貴重ですので、価値は高いです。
★2023年度版の主な講義・好きだった講義:
◯スタンダード演習の講義
◯数Ⅲ演習の講義
4ページ/例題3問ほどの講義。
講師オリジナル問題?が使われており、受験数学とは微妙に毛色が異なる「講義のための問題」を扱うため、興味深いものが多い。
数学が得意になりたいのならば、こういう変わり種の問題にも数多く触れるべきで、その中でも特に良質な問題がオリジナル問題として扱われる、といった印象を受ける。
お気に入りは2023年12月号(数式演習)のⅠAⅡB講義。食塩水の問題が逆に新鮮だった。
◯図形のミカタ
図形問題の解法のまとめ。
座標/複素数/ベクトル/幾何などジャンル別特集
各4ページで、6月〜翌2月の隔月掲載(全5回)
各例題5問+演習3問ほど
◯共通解(ミニ講義)
共通解の問題特集。
2ページの単発記事。4月号掲載。
例題3問
学習効果は高いと思う。
◯約数の個数/総和(ミニ講義)
約数の問題特集。
2ページの単発記事。5月号掲載。
例題2問で、オリジナル追加問題あり。
学習効果が特に高いと感じた。
◯受験数学ダイアログ(8月号)
生徒2人と先生の対話文形式で入試問題を解いていく。何回か掲載される。
対話文形式のため、試行錯誤の過程や定石への適用などが特に分かりやすい。
8月号は定積分と不等式がテーマ。
2023東大(第1問)と2023東工大(第1問)を扱う。
◯2022年12月号(数式)の講義
循環小数の2進数表記に感動した。
例題3問。
◯読み物2:ガチの読み物
大学数学の話だったり、物理の話など。それらに全く関係のない話題もいくつかあります。
学術的な話題はだいぶ難解なネタになりますが、一般的な読み物は非常に読みやすいものばかりです。
ほかに受験体験記などもあります。これも日々の学習のモチベーションになることでしょう。
◯参加型コンテンツ
エンドコンテンツがユーザー間のオンライン対戦や交流になるというのは、ゲームではよくある話ですが、月刊大数でも同じです。
問題としては、難易度C〜D問題の点数を競う「学コン」と、解答や考察を編集部に送る「宿題」があります。
いずれも難しく、この記事で新たに月刊大数に手を出すことになる方にはおそらく無縁のコンテンツになります。
一応、2ヶ月後に、解答解説が再掲問題とともに掲載されますので、軽く手を付けてみて、解答を眺めるくらいはしても良いでしょう。解答を読んで理解するのも大切な訓練です。解答を読めない人間に、答案が書けるはずがありませんからね。
また、「接点」と題した、読者のつぶやきを集めたコーナーもあります。
ガチでしょうもない素朴なつぶやきばかりで、受験で疲れた心がほっと癒やされます。
現在、月刊大数では「接点」の投稿を大募集しているようです。僕がこの記事を書いているのも、半分くらいは「接点賑わってほしいな」という想いからです(これはガチ)。
みなさんも月刊大数を買って、是非とも接点を投稿してみてほしい。ちなみに私も見てますよ。
使い方/よくある質問
最後に、月刊大数の使い方を、よくある質問と一緒にまとめてみます。
◯参考書ルートのどこにいれる?
中身が幅広いため、使い方によってルートへの入れ方も変わってきます。
個人的には、問題集や参考書での学習の補強教材として考えるものだと思われます。
「参考書をもう1冊やるのもアレだけど、同じやつを何周も繰り返したくない!」というワガママ受験生に向けて、1年間の合計で、各レベル帯に応じて0.5冊~0.8冊分くらいの文量が用意されています。(もちろん、全問題を2周解く必要はないですが、怪しかった問題の復習等はしっかりやる前提です)
参考資料として、以下に個人的な難易度感をまとめてみました。
スタンダード演習のB問題と日々の演習のB問題が同じ難易度に感じられないため、BとCの中でもさらに細分化してみました。
問題集などは生徒に使わせた/使っていたものたちから抜粋しました。
これらは「全ての問題に目は通している」のですが、「全ての問題を解いた」わけではないため、難易度感は印象によるものが大きいことを断っておきます。
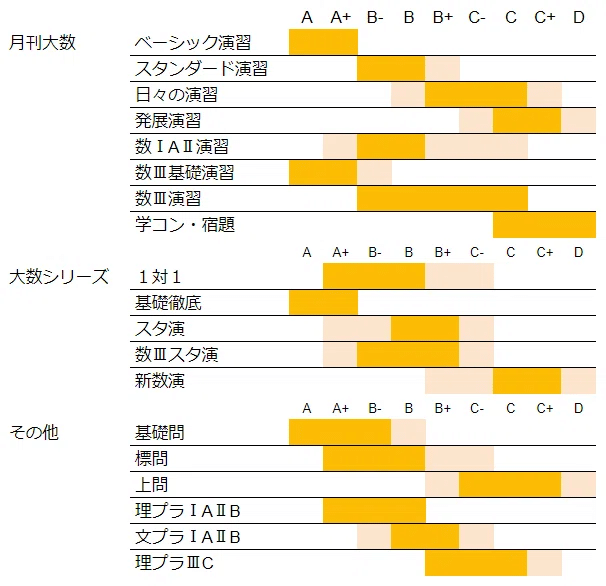
◯どうやって解くか?
制限時間を気にしつつ、大問を完答することにこだわって演習・復習をしてください。月刊大数を扱う理由は「大問を完答して、ライバルに差をつける」ためです。
完答する際には、「どこが問題のヤマ場か」を意識することが肝要です。問題が難しくなる瞬間(ヤマ場)を乗り越えられるように、そういった意識を常に持っておきましょう。
ここからは、よくある(であろう)質問です。
質問1:書店に売ってないんだが?
通販を利用します。
公式通販で過去2年分ほどが発売されています。
安く求めるならメルカリ等で中古品を探します。
過去分をアマゾンで買うことだけはオススメしません!公式通販の存在を知らない情弱を狙った転売業者であり、割高です。
公式通販URL↓
質問2:量多すぎね?
実際、だいぶ量があるのは確かです。
以下にいくつかの解決案を挙げます。
案1:冊数を絞る/演習を絞る
冊数を絞るなら、5〜11月号か、12〜2月号のどちらかに取り組みましょう。
単元別学習に取り組みたいのなら5~11月の演習をこなします。
合計7ヶ月分になります。これでも多いのであれば、さらに苦手単元/頻出単元に絞っても良いかもしれません。
個人的には、月刊大数は苦手分野の克服教材としてはちょっとリスクが高いようにも感じますので、得意単元や頻出単元のプラスワン的に扱っていくのがベターです。
単元別学習はOK、あるいは過去問がたくさん用意できない大学を志望しているようなパターンの場合は、過去問の合間に12月号~2月号の総合演習を挟んでいきましょう。
12月~2月号で、B問題に60問、C問題に40問ほど触れることができます。B問題メインでCをスルーするにしても、CメインでBを前座的に扱うにしても、1ヶ月~1.5ヶ月で丁度よい文量のハズです。物足りなければさらにもう1年分過去のものも追加すれば良いです。公式通販にて過去2年分が販売されています。
出題傾向によっては、解かなくて良い(優先度が低い)演習が出てくる可能性もあります。
例えば工業系の大学は、確率や整数などがあまり出題されず、数Ⅲの微積分が全体の半分以上で出題されたりします。
案2:1年以上かけて取り組む
案1では取り組む問題数を減らす提案をしましたが、本当はあまりおすすめしません。
そもそも月刊大数を使う目的は「あえて雑多に問題に触れることで、他の受験生に差をつけるため」です。他の受験生が手薄になっているところを上手に稼ぐからこそ、数学でライバルに差をつけられるのであって、問題数を減らしてしまえば本末転倒です。
というわけで、こちらの案が本命です。
演習の難易度別に2周~3周します。
新高2の人に特にオススメできるやり方です。夏休み頃からスタートして、入試本番までに全問題を終えるコースになります。
先に買わなければならない都合上、1年古い年度の問題で演習することになりますが、よっぽど問題ないでしょう。
1年半かけて月刊大数を使用した指導実績あります↓
■プロフィール
・公立高校(偏差値60後半)→東大文3
・部活は高3の5月まで(テニス部、週3+月1〜2で試合)
・もともと数学は可もなく不可もなく/好きでも嫌いでもない
・数学を入試での得意科目とするために、高2秋から入試対策に取り組む
■使用:2022/4~2023/2と、2023/12~2024/2
・浪人生の兄が使っていた2022年度版の月刊大数を高2秋から使用
■問題レベル別に計3周
◯1周目
・ベーシック演習 2022年度分
・数ⅠAⅡ演習 4月-7月(計算、関数基礎、方程式、不等式)
◯2周目
・スタンダード演習 2022年度分
・数ⅠAⅡ演習 2022年度分(1週目の残り)
◯3週目
・日々の演習 2022年度分
・2023年12月-2024年2月分
■進め方
・市販の問題集と組み合わせ、ひとつの分野を1〜3週間かけて、集中的にやり込んでいく。
・同じB問題でも、難易度感は月刊スタ演習≦新スタ演なので、先に月刊誌から進めていった。
◯参考書ルート
・1周目+『入試数学の基礎徹底』(高2・9月〜10月)
・1対1 ⅠAⅡB(11月〜1月)
・2周目+『新スタ演』(高2・2月〜高3・7月)
・3周目+過去問+冠過去問(8月〜翌2月、ただし12月から共テ対策で社会に注力し、一時中断)
・そのほか、学校の授業では『メジアン数学演習』を扱っている
■各段階ごとの模試の成績推移
・僕が記憶する限りの、大まかな成績推移です
・上の学習進度と照らし合わせて、どの時点でどの成績になるのか見てください
・冠模試はだいたいの点数
◯高2
7月進研……55/100点・偏差値60
10月進研……70/100点・偏差値65
1月進研……160/200点・偏差値65
◯高3
8月全統……180/200点・偏差値75
夏冠模試……45/80点(D判定。社会が足を引っ張っていた)
10月何か……195/200点・偏差値80
秋冠模試……60/80点(A-B判定。社会が一気に伸びてきた)
◯入試
共テ……194/200
2次試験……68/80
■総論
・難化した年の割には本当に上出来
・そもそも文系数学は分かりやすく差がつくが、今年のセットは特にしっかり差をつけることができた(と思う)
・日々の演習の難易度と、今年の東大文系の難易度感がほぼ一致していて良かった。関連問題も何問か触れていたはず
・傾向に縛られすぎず、幅広く演習を積めたのが良かった(実際、対数の問題が一番サクッと完答できたらしい。確かに一般的にはよくある問題だよね)
質問3:良かった号を教えて
6月・7月の数ⅠⅡ演習。
方程式全般、不等式全般を扱う単元です。
「ただの複雑な4次方程式」など、他の問題集だと単元分けしにくいせいかスルーされがちな問題も収録されているのが良かったです。
特集は整数(10月号)です。ガウス記号や2進法など、手薄な問題が結構たくさん載っていてよかった。
数Ⅲ演習は12月号の数式総合演習が好みの問題が多くてお気に入りでした。
あとは東京学芸大の推薦入試問題とか(2月号だったかな?)も印象に残っています。
文量が長くなったのと十分魅力を語ったと思うので、ここで終わりにして投稿します。
月刊大数、基本的な要素を一通り押さえた人全員に使える参考書ですので、気になる人は使ってみてください。
この記事が気に入ったらサポートをしてみませんか?
