
線形代数の擬似逆行列について
はじめに
皆さん、こんにちは。
今回は、線形代数における擬似逆行列というものについて、話をさせていただこうと思います。
機械学習における、回帰分析などと相性が良い考え方になります。
線形代数や、機械学習について
機械学習や、線形代数などについては、以下の記事にもまとめていますので、よければ参照下さい。
単位行列と逆行列
上記の線形代数についての記事にも書いてありますが、擬似逆行列について話す前に、単位行列と逆行列について話をさせていただきます。
先ず、単位行列とは、数字の1のようなもので、これはベクトルや行列に単位行列を掛けると、出力として、元のベクトルや行列が、そのまま計算されるものです。
具体的には、縦の要素数と、横の要素数とが等しい正方行列で、かつ対角成分のみが 1、残る成分が 0 で構成されるものです。
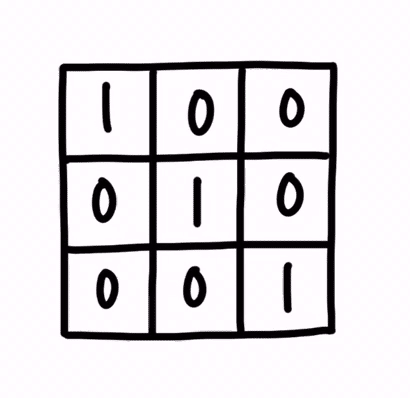
この行列は、I という文字で表されることが一般的です。
アルファベットの I(アイ)です。
例えば、ベクトル a については、「I ✕ a = a」や「aᵀ ✕ I = aᵀ」となります。
或いは、行列 B については、「I ✕ B = B」、「I ✕ Bᵀ = Bᵀ」、「Bᵀ ✕ I= Bᵀ」、「B ✕ I = B」となります。
イメージで確認すると、以下となります。

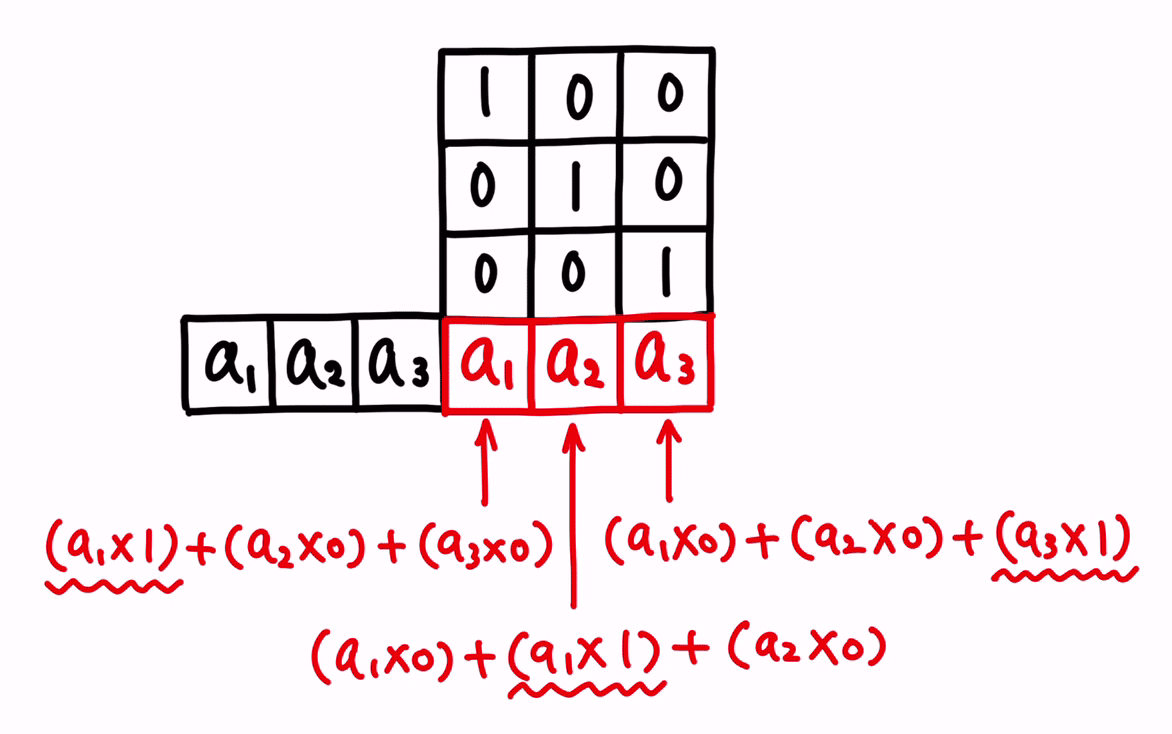

これが単位行列の概念となります。
次に、逆行列ですが、単位行列と密接な関係を持ちます。
数式としては、例えば、行列 A の逆行列は、A⁻¹ と表記します。
そして、行列 A と、逆行列 A⁻¹ とは、掛け合わせると、単位行列 I になります。
つまり、「AA⁻¹ = I」ということです。
また、逆行列 A⁻¹ は、行列 A を元に算出されます。
行列 A に対して掛け合わせると、単位行列になるような行列を無理矢理逆算するような形で求めます。
尚、単位行列同様、縦の要素数と、横の要素数とが等しい正方形の行列です。
イメージとしては、以下です。
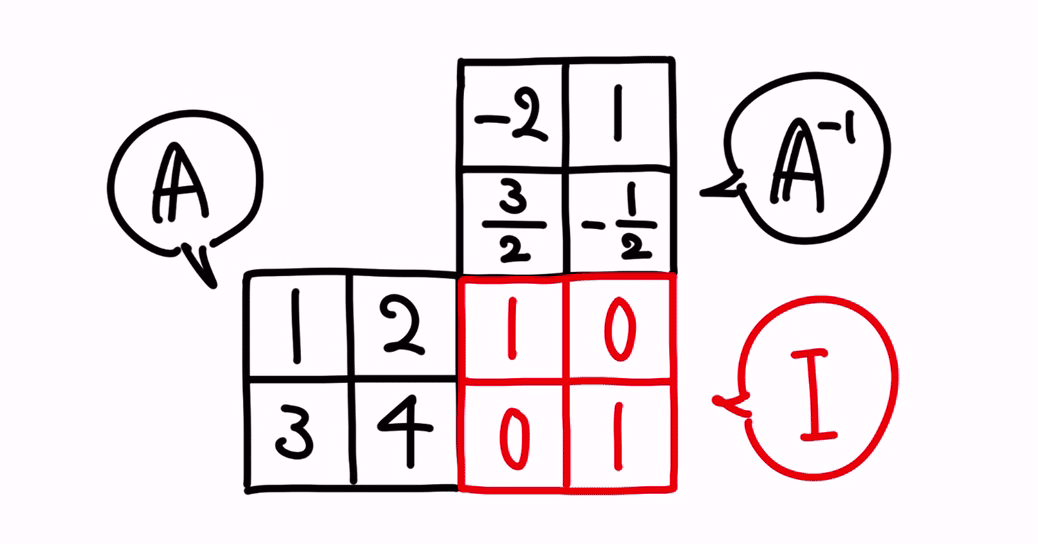
また、面白いことに、「AA⁻¹ = I」だけでなく、「A⁻¹A = I」の関係性も成り立ちます。

こんな形で、リバーシブルに対応することができます。
尚、逆行列については、なかなか複雑なアルゴリズムで求める必要があるのですが、python の numpy ライブラリを使ってしまえば、瞬時に算出できます。
その為、プログラムを用いた計算をする場合には、逆行列を求める計算負荷について、考える必要はありません。
擬似逆行列とは
さて、単位行列と逆行列を理解してもらった上で、次に、擬似逆行列の話をさせていただきます。
擬似逆行列は、逆行列と同じ性質をもちます。
それは、つまり、掛け合わせると単位行列になる、という性質です。
数式としては、例えば、行列 A の疑似逆行列は、A⁺ と表記します。
そして、行列 A と、逆行列 A⁺ とは、掛け合わせると、単位行列 I になります。
つまり、「AA⁺ = I」ということです。
或いは、「A⁺A = I」ということです。
しかし、注意しなくてはならないのは、「AA⁺ = I」と「A⁺A = I」の両方を同時には満たさないということです。
また、擬似逆行列は、逆行列のように縦と横の要素が等しくある必要がありません。
そこが逆行列 A⁻¹ と異なるものです。

擬似逆行列の要領は分かってもらえたかと思います。
次に、擬似逆行列の作り方について説明します。
擬似逆行列は、式にすると「A⁺ = (AᵀA)⁻¹Aᵀ」という形で表します。
図にすると以下となります。

一見、ややこしいのですが、整理してみると、実は結構単純です。
「A⁺A」の式に、「A⁺ = (AᵀA)⁻¹Aᵀ」を代入してみると、「(AᵀA)⁻¹AᵀA」となります。
ここで、「B = AᵀA」と置くと、「(AᵀA)⁻¹AᵀA」という式は、「B⁻¹B」という風に表現することができます。
ここで、B という行列は正方行列であり、「B⁻¹B = I」となります。
つまり、B を代入する前の式も「(AᵀA)⁻¹AᵀA = I」となります。
イメージにまとめると以下です。

尚、ここで、必ず「N > D」である必要があります。
仮に、「N < D」である場合、行列 B は実は逆行列の計算ができません。
それは、行列 B が、正則行列でなくなってしまう為です。
