見出し画像

NIRSの信号処理について考えてみる〜④フーリエ変換からウェーブレット変換へ〜

七丸

フーリエ変換の限界と短時間フーリエ変換

前回の記事ではフーリエ変換について説明をしたが，フーリエ変換は万能なものではなく，これを行うと時間情報が失われてしまう。具体的には，「振幅と時間」の情報を「振幅と周波数」の情報に変換するため，「どの波がいつ発生したのか」を知ることはできない（図1）。

図1　フーリエ変換の限界

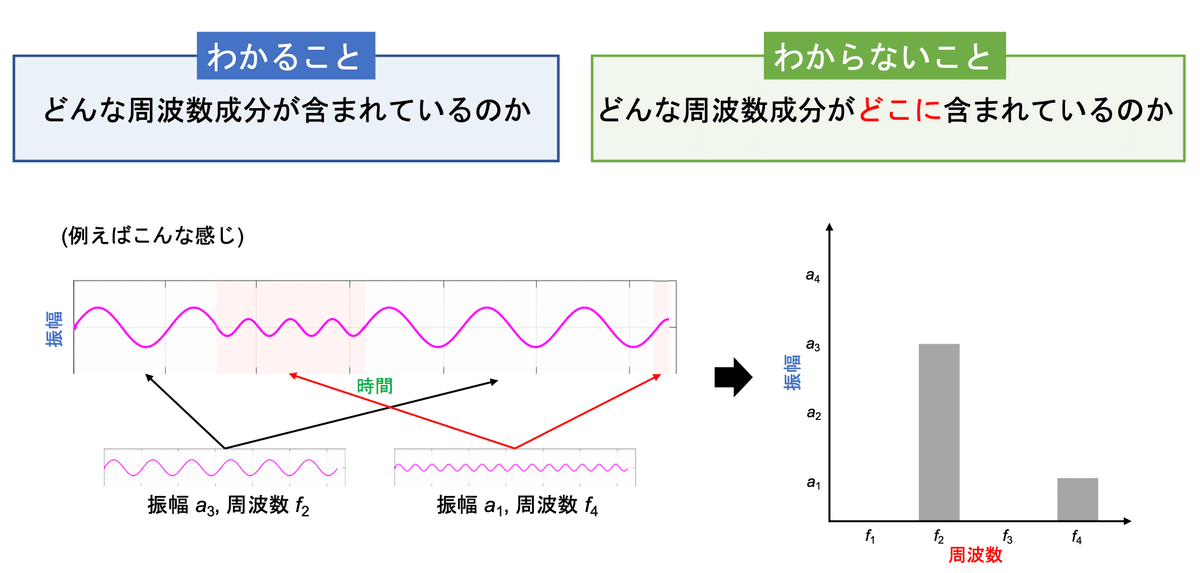
この「いつ発生したのか」を知るために，「短時間フーリエ変換」というものが利用できる。これは，変換する範囲を区切ることで時間情報を得るというものである（図2）。

図2　短時間フーリエ変換のイメージ

しかしながら，短時間フーリエ変換もまた万能なものではない。例えば，波の変化をより細かく見るために変換する時間幅を狭めると，周波数分解能（周波数の検出性能）が低下する。これは「不確定性関係（不確定性原理）」と呼ばれ，具体的には「時間分解能と周波数分解能はトレードオフの関係にある」というものだが（図3），数学的に内在する問題であるためこれを解消する方法はないとされている。

図3　フーリエ変換における不確定性関係のイメージ


時間も周波数も上手に見るには

実際に周波数解析をしてみるとわかるのだが，多くの場合は時間情報と周波数情報とは常に等しく重要であるというわけではない。高周波帯域においては時間情報の詳細が，低周波帯域においては周波数情報の詳細が求められるのではないだろうか（図4）。

図4　時間を優先するか周波数を優先するか

このような，周波数に応じて分解能を変化させるという実に都合のよい方法の1つに「ウェーブレット変換」というものがある。

ウェーブレット変換では，極めて簡単な説明ではあるが，基底関数（ベースとするもの）としてマザーウェーブレットという波のかけらを決定し，これを解析したい波に対して「シフト（平行移動）」と「スケーリング（拡大縮小）」を繰り返して解析対象との相関をとるということを行う（図5）。なお，マザーウェーブレットには様々なものがあるが，明確な選択基準があるわけではないという。

図5　ウェーブレット変換の概要とスケーリングのイメージ

さらに簡単に言えば，高周波 → 低周波という流れの場合では，

  • マザーウェーブレットを決定する。

  • マザーウェーブレットを縮める。

  • 縮めたマザーウェーブレットを解析対象の波の始まりから終わりに向かって平行移動させながら，マザーウェーブレットと解析対象の波との各部分での類似性を見る。

  • 最後まで行ったら縮めたマザーウェーブレットを伸ばして同様の手順を行う。

  • これを繰り返す。

特にシフトについては動画の方がわかりやすいと思われるため，以下の動画（10:45–11:16 の部分）を紹介する。

「YouTube 【Andrew Nicoll】The Wavelet Transform for Beginners」

さらに細かく言えば，マザーウェーブレットのシフトとスケーリングを連続的に行う「連続ウェーブレット変換（CWT: Continuous Wavelet Transform）」と，これを離散的に行う「離散ウェーブレット変換（DWT: Discrete Wavelet Transform）」が存在するが，これらについては僕が理解し切れていないため，ここではこれらの特徴を列挙するに留める（図6）。

図6　CWT と DWT の特徴


ウェーブレット変換の実演

実際に NIRS データを用いて，どのような波がいつ発生したのかを MATLAB で調べてみる。ここでは，サンプルデータとして，応答成分とする約 0.025 Hz のデータにノイズとして応答成分付近の周波数成分を加えたものを使用する（図7）。

図7　サンプルデータ

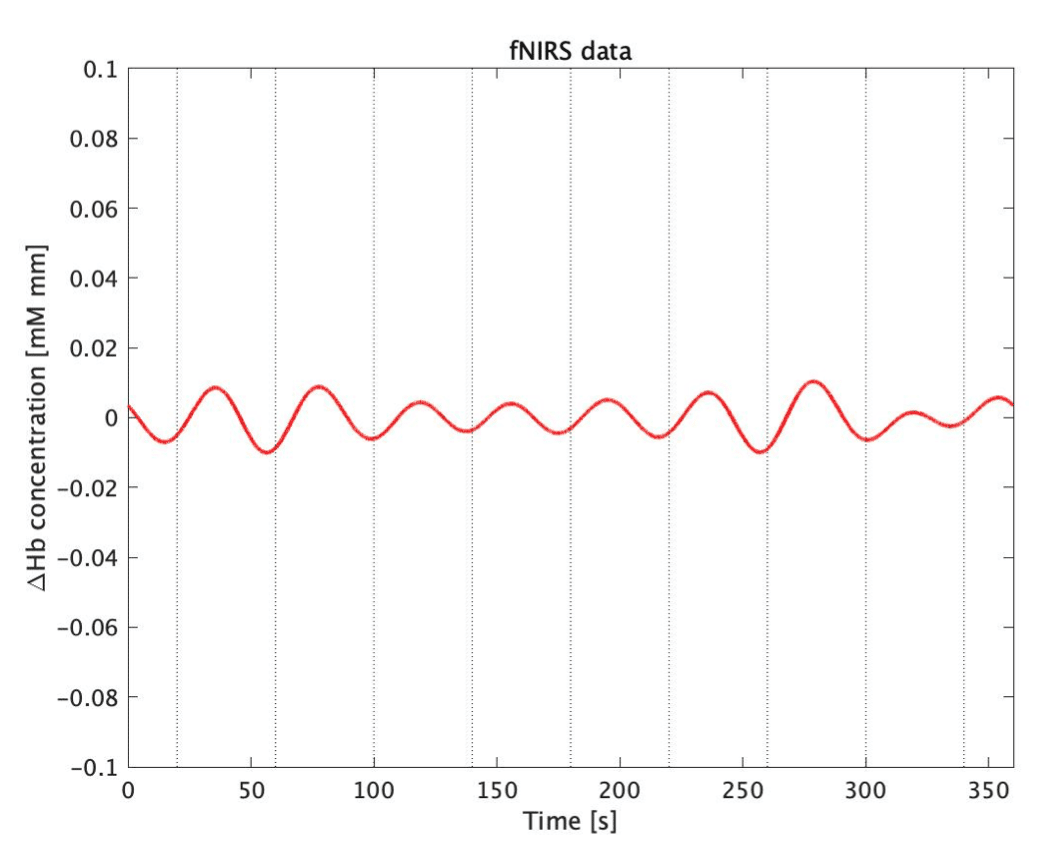
MATLAB のヘルプセンターを参考に，スカログラム（時間–周波数解析の結果の図の一種）を出力する（図8）。これは以下のようなコードで作成することができる。なお，このコードではマザーウェーブレットは "Morse" が使用される。

% fs は前回までの記事と同じくサンプリング周波数を表す。

x ＝ data;

num = 1:length(x);
sig = x(num, 1);
fb = cwtfilterbank('SignalLength', length(x), 'SamplingFrequency', fs);
[cfs, frq, coi] = wt(fb, sig);
t = (0:length(x)-1)/fs;
pcolor(t, frq, abs(cfs));
shading interp;
hold on
plot(t, coi, 'w-', 'LineWidth', 2)
hold off
xlabel('Time (s)')
ylabel('Frequency (Hz)')
c = colorbar;
c.Label.String = 'Magnitude';
ylim([0.01 0.1])
title('Scalogram')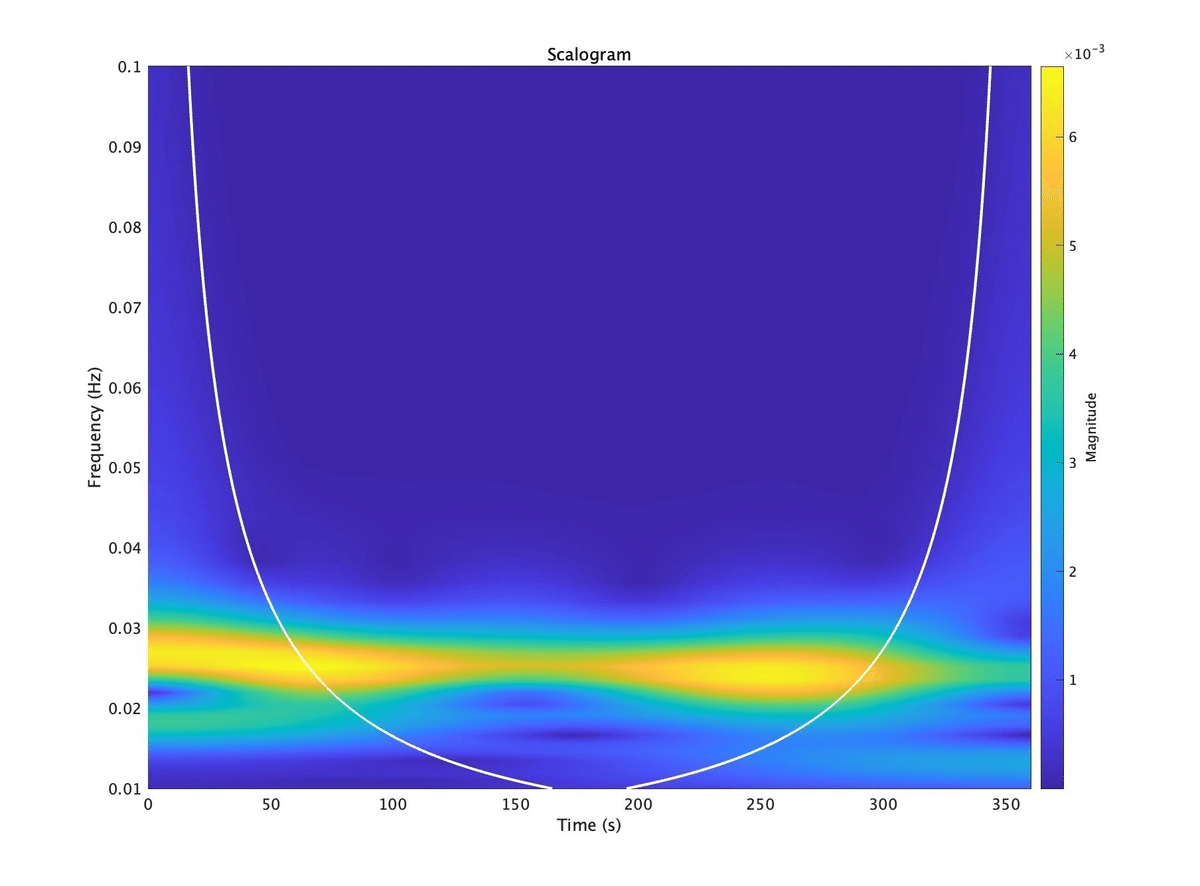
図8　サンプルデータ（図7）のスカログラム

図9から，0–360 秒にかけて一貫して約 0.025 Hz の成分が含まれていることがわかる。さらに，振幅との関係に注目すると，図7において振幅が大きい部分では図8でも振幅が大きいものとして表示されている。

なお，図8に表示されている白線は「円錐状影響圏（cone of influence）」の境界線であり，白線の外側における結果は厳密なものではないことを示している。これは，変換対象の波の両端付近においては完全なマザーウェーブレットを当てはめることができないためであると考えられる。特に低周波帯域においてはマザーウェーブレットは横長に伸ばされているため，これがさらに顕著なものになる。ゆえに，低周波帯域の円錐状影響圏は高周波帯域よりも大きくなると考えられる。

余談ではあるが，短時間フーリエ変換でも図9と類似の図を作ることができる。ただし，短時間フーリエ変換の場合は「スペクトログラム」，ウェーブレット変換の場合は「スカログラム」と呼ばれる。


まとめ

  • フーリエ変換：どんな波が含まれているかがわかる。

  • 短時間フーリエ変換：どんな波がどこに含まれているかがある程度わかる。

  • ウェーブレット変換：どんな波がどこに含まれているかがいい感じにわかる。


参考文献

いいなと思ったら応援しよう！